轨迹规划(Trajectories Planning)主要指考虑实际临时或者移动障碍物,考虑速度,动力学约束的情况下,尽量按照规划路径进行轨迹规划。
轨迹规划的核心就是要解决车辆该怎么走的问题。轨迹规划的输入包括拓扑地图,障碍物及障碍物的预测轨迹,交通信号灯的状态,还有定位导航(因为要知道目的地是哪才能规划路径)、车辆状态等其他信息。而轨迹规划的输出就是一个轨迹,轨迹是一个时间到位置的函数,就是在特定的时刻车辆在特定的位置上。
在本篇分享中,我们有请高级架构师 Zhang Yajia 为大家分享在百度 Apollo 平台上,轨迹规划算法的技术方案。
轨迹规划综述
轨迹规划的目标是计算出安全、舒适的轨迹供无人驾驶车辆完成预定的行驶任务。安全意味着车辆在行驶过程中与障碍物保持适当的距离,避免碰撞;舒适意味着给乘客提供舒适的乘坐体验,比如避免过急的加减速度,在弯道时适当减速避免过大的向心加速度等等;最后,完成行驶任务指规划出的轨迹要完成给定的行驶任务,不能因为过于保守的驾驶导致不可接受的行驶时间。
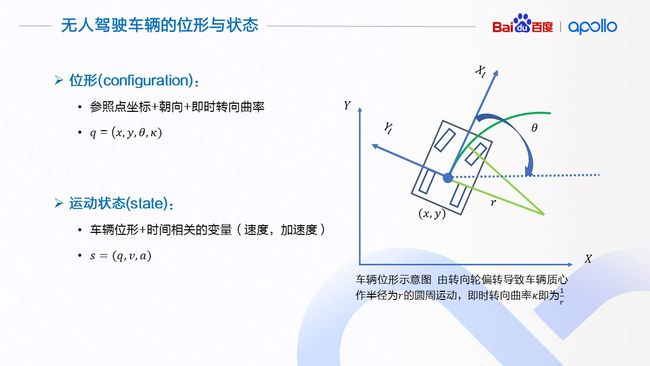
无人驾驶的位形与状态
我们这里对轨迹规划问题作正式的定义。首先,我们介绍两个机器人领域的概念:位形(Configuration)是在所研究的规划问题中,能够唯一性的表达机器人状态的最小一组变量。变量的数量称为位形的维度。这里需要注意的是,位形空间的维度,即使对于同一个机器人来讲,所研究的问题不同,维度也是不同的。比如,对一个人形机器人来讲,如果规划问题是在三维空间中移动,位形需要由参照点的变换矩阵,关节的伸展角度组成;如果规划问题是作物体的操作(Manipulation Planning),则在前面问题位形空间的基础上,还要增加机器人手指关节的伸展角度等。
对于无人驾驶车辆来讲,最简单的位形描述需要使用3个变量:车辆某个参照点的坐标(x, y),以及车辆的朝向θ来表达车辆的构型,这也是很多参考文献中,对于非和谐车辆系统的位形表达方式。对于我们专门为有人乘用的无人驾驶车辆作轨迹规划的问题来讲,更好的位形组成在上面的3个变量基础上加入车辆的即时转向曲率κ:如果车辆的导向轮保持一定的角度,车辆会做圆周运动。这个圆周运动的半径就是即时转向曲率 κ。加入κ,有助于控制模块获得更准确的控制反馈,设计更为精细平稳的控制器。
轨迹规划的定义
轨迹规划的正式定义,计算一个以时间t为参数的函数S,对于定义域内([0, t_max])的每一个t,都有满足条件的状态 s:满足目标车辆的运动学约束,碰撞约束,以及车辆的物理极限。
轨迹规划问题的难点
轨迹规划是一个复杂的问题,首先,规划上加入了速度与时间的信息,增加了规划的维度。其次,由于车辆是非和谐系统,具有特殊的运动学约束条件。举个例子,车辆不能独立的横向移动,需要纵向移动的同时才能获得横向偏移。躲避障碍物,特别是高速动态障碍物,也是一个比较困难的问题。对于搭载乘客的无人驾驶车辆来说,非常重要的一个要求(在本人看来可能是最重要的)是舒适性,规划出的轨迹必须做到平滑,将影响乘客舒适度的因素,比如加速度,向心加速度等等,保持在能够容忍的范围。
另外,对于无人驾 驶车辆来讲,为了处理多变的行车环境,轨迹规划算法需要以短周期高频率运行,对算法的计算效率也提出了要求。
Apollo 中轨迹规划策略
在 Apollo 平台中,为了解决规划问题,尤其是从降低计算的复杂性上,我们采取了对轨迹的路径与速度规划分离的方式。即先确定路径,也就是轨迹的几何形状,然后在已知路径的基础上,计算速度分配。使用这种策略,我们将一个高维度的轨迹规划问题,转换成了两个顺序计算的低维度规划问题:路径规划,借助中间变量路径的累计长度 s,先求解 s 映射到几何形状(x, y, θ, κ)的路径函数;速度规划,再求解时间 t,映射到中间变量 s,与 v,a 的速度函数。
路径规划的目标
前面提到 Apollo 轨迹规划的策略,我们先看路径规划在这种策略下需要解决的问题:
-
路径需要有足够的灵活度,用来对复杂城市环境中的障碍物进行避让。
-
路径的几何特性需要平顺变化,这样车辆在沿路径行驶时才能够保证舒适性。
-
路径的规划需要遵守车辆的运动学限制条件,比如,路径的曲率、曲率变化率需要限制在符合目标车辆属性的范围之内。
-
由于我们在 Apollo 平台中采用了路径/速度分离的策略,在路径规划时也需要考虑到当前车辆的运动状态而适当的调整车辆的几何形状。比如在做较大的横向运动的时候,低速和高速下,我们需要不同的几何形状来保证横向运动的舒适性。
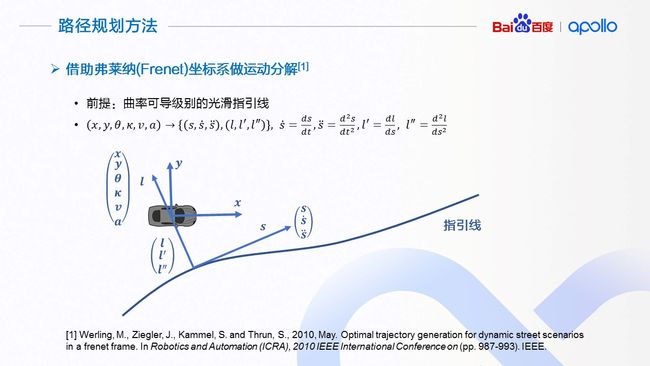
路径规划方法
在路径规划中,我们借助于弗莱纳坐标系,将当前车辆的运动状态(x, y, θ, κ, v, a)做分解。使用弗莱纳坐标系的前提是具有一条光滑的指引线。一般情况下,我们可以将指引线理解为道路中心线,车辆在没有障碍物情况下的理想运动路径。我们这里的光滑的指引线是指指引线的几何属性可以到曲率级别的光滑(曲率可导)。指引线的光滑性至关重要,因为其直接决定了在弗莱纳坐标系下求得轨迹的平顺性。在 Apollo 平台上,我们实现了多种平滑指引线的计算方法,在今天的分享中就不展开介绍了,有兴趣的同学请查阅相关代码(或者我们再进行一次以指引线为主题的分享。
在给定一条光滑指引线上,我们按照车辆位置,将其投影到指引线上,以投射点为基础,将地图坐标系下当前车辆的运动状态(x, y, θ, κ, v, a)进行分解,获得沿着指引线方向的位置,速度,加速度,以及相对于指引线运动的位置, “速度”, “加速度”。这里打引号的原因是横向的“速度”、“加速度”并非通常意义上位移对时间的一阶/二阶导数,而是横向位移对纵向位移的一阶/二阶导数,它们描述了几何形状的变化趋势。
在弗莱纳坐标系下作轨迹规划的优点
在弗莱纳坐标系下做运动规划的好处在于借助于指引线做运动分解,我们将高维度的规划问题,转换成了多个低维度的规划问题,极大的降低了规划的难度。另外一个好处在于方便理解场景,无论道路在地图坐标系下的形状与否,我们都能够很好的理解道路上物体的运动关系。相较直接使用地图坐标系下的坐标做分析,使用弗莱纳坐标,能够直观的体现道路上不同物体的运动关系。
路径规划-分段加加速度优化算法
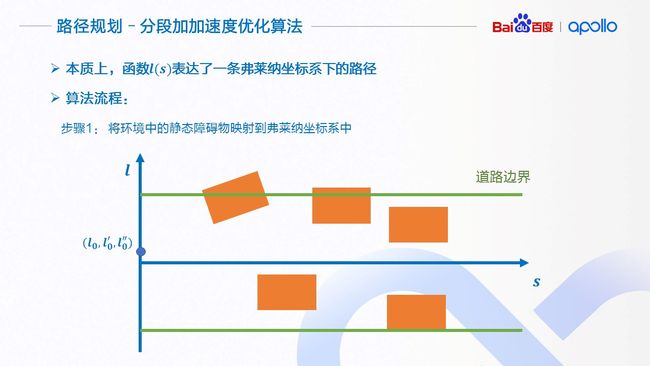
在弗莱纳坐标系下的函数l(s),表达了以指引线为参考,相对于指引线的几何形状;通过转换到地图坐标系下,就表达了在地图坐标系的路径。所以,本质上,路径规划问题在弗莱纳坐标系下,就是一个计算函数l(s)的过程。
为了解决这个问题,这里介绍由我提出的分段加加速度优化算法(Piecewise Jerk Path Optimization Algorithm)。我们先来看一下算法的流程:
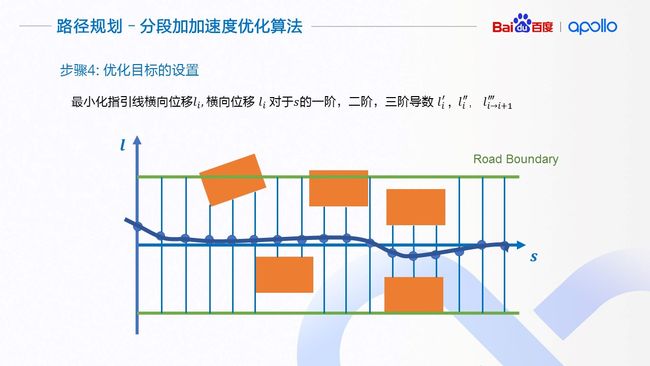
第一步,我们将环境中的静态障碍物从地图坐标系映射到依据指引线的弗莱纳坐标系下(红色方框)。
第二步,沿指引线的s轴方向,使用Δs将s方向等距离离散化。根据障碍物的信息、道路的边界,计算出每一个离散点所对应的可行区域(l_min^i,l_max^i )。为了方便描述,我们将无人驾驶车简化成一个点。为了避免碰撞,在计算可行区域的时候可以留出适当的缓冲区间。
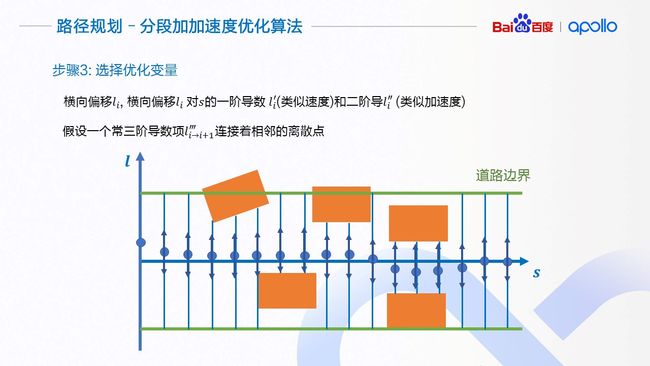
第三步,我们介绍优化算法使用的优化变量。对于每一个离散点i,我们将该点的横向偏移 l_i,横向偏移相对于s的一阶和二阶导数 l_i^′ 和 l_i^″作为优化变量。l_i^′ 和 l_i^″可以近似理解为横向运动的“速度”与“加速度”。他们的大小决定了车辆靠近与偏离指引线的趋势。我们假设每两个离散点之间,有一个常三阶导数项l_(i→i+1)^‴连接着相邻的离散点, 这个“常”三阶导数项可以由相邻的二阶导数通过差分的方式计算得到。在优化的迭代过程中,l(i→i+1)^‴ 会随着相邻点li^″ 与l_(i+1)^″ 的变化而变化,但l_(i→i+1)^‴在两个离散点之间会保持不变。
这也是我们算法的得名,分段的加加速度算法。
第四步,设置优化目标。首先,对于路径来讲,在没有环境因素影响的情况下,我们希望它尽可能的贴近指引线。对于一阶、二阶与三阶导数,我们希望它们尽可能的小, 这样可以控制横向运动的向心加速度,保证路径的舒适性。
算法完整描述
下面,我们回顾一下这个算法,算法的输入由四个部分组成:
-
光滑的道路指引线,用于在弗莱纳坐标系下的运动分解。
-
当前无人驾驶车辆的运动状态,包括位置、朝向、即时转向、速度与加速度。车辆运动状态会依照光滑指引线进行分解。
-
环境中静态障碍物的信息,投影到指引线上。
-
车辆自身的属性,运动学模型等,用于计算优化过程中合理的变量限制条件。
算法的变量每一个离散点的横向位移,横向位移对指引线纵向长度 s 的一阶、二阶导数,对于有 n 个输入点的问题,优化变量有 3∗n 个。对于限制条件,首先横向位移li需要在相对应的安全区间之内(l_min^i,l_max^i )。对于 l_i^′, 〖l_i〗^″, l(i→i+1)^‴的取值范围,需要根据当前车辆移动速度, 车辆的动力学模型计算,这涉及到具体的车辆模型,这里我们就不展开介绍了。
一个非常关键的约束条件是路径的连续性。我们假设相邻两点之间有一个常三阶导数量 l_(i→i+1)^‴来连接,我们需要确定经过这个常三阶导数量l(i→i+1)^‴,相邻两个点的l, l^′, l″的数值能够吻合。举个例子,两个点之间就好比可以拉伸的绳子,l(i→i+1)^‴决定了可以拉伸的程度,这两个式约束决定了在绳子拉伸的过程中保证绳子不被拉断。
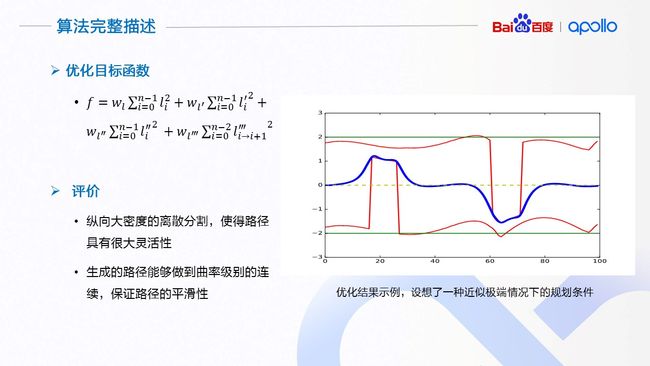
算法的优化目标,是减小横向位移的零阶,一阶,二阶和三阶导数,使路径尽可能贴近指引线的同时保证舒适性。当然,我们也可以根据需求,选择性的加入与边界距离的优化目标,使车辆与障碍物保持适当距离。分段加加速度算法由于其大密度分段的特性,使得能够表达的路径具有很高的灵活性,能够解决城市道路中(特别是国内拥挤的环境J)的路径规划问题;并且,由于是以加加速度级别的控制变量来改变路径的形状,能够做到曲率级别的连续性,保证了路径的平滑舒适。
路径规划的目标
下一步,我们来看怎样为计算出的路径分配速度。对于速度规划,我们有如下要求:
-
速度分配具有灵活性,能够避让复杂、拥挤的城市环境中的众多移动障碍物。
-
速度分配需要遵守车辆运动学的限制条件, 比如最大速度、加速度、加加速度等,确保规划出的轨迹车辆实际可以执行。
-
规划的速度分配需要遵守考虑交通法规的限制,在限速范围内规划。
-
规划的速度分配需要完成到达指定位置或者指定速度的任务,并且在保证舒适度的前提下,完成时间尽可能的短。
路径规划的策略
在 Apollo 平台的实现中,我们采用了结合启发式速度规划和分段加加速度算法相结合的方式来解决速度规划问题。启发式速度规划提供考虑了动静态障碍物、路径几何信息、道路信息、舒适度、目标速度和地点多种因素综合下的速度规划粗略估计;分段加加速度算法对启发是速度规划提供的粗略分析进行平滑,输出安全舒适的速度分配。
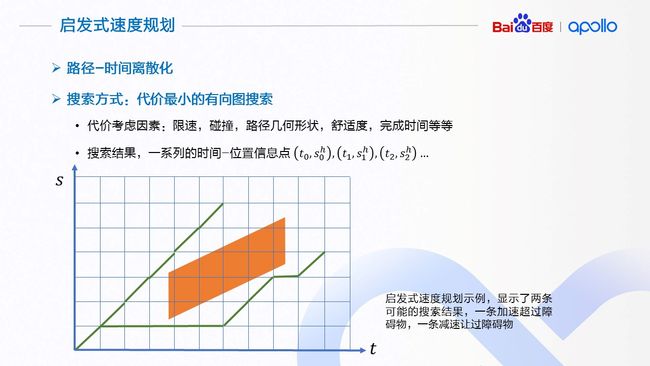
在启发式速度规划中,我们采用了一个非常好的分析工具,路径-时间障碍物图(Path-Time Obstacle graph)。路径-时间障碍物图非常适合在确定了路径的情况下,考虑动静态障碍物的规避问题。这个分析工具的核心思想就是将考虑了本车和周围障碍物几何形状和预测轨迹的情况下,将障碍物的轨迹投影到已经确定的本车路径上。障碍物所代表的含义是在何时(t)与何地(s)本车会与障碍物发生碰撞。
启发式速度规划
在 Apollo 的实现中,路径-时间障碍物图根据时间轴t和沿路径的累计距离s离散化,形成等距离、等时间的网格状图。然后根据我们的需求,将各种因素使用不同的权重,建模成一个单一熟知的代价函数,每一个网格的节点会赋予一个代价,相邻网格之间的边也视为代价的一部分,用来建模加速度。整个过程可以看成是一个图搜索的过程,搜索出一个代价最优的路径。搜索的结果就是一系列的路径距离与时间的序列,代表何时(t),我们期望无人驾驶车到达何地(s).
分段加加速度平滑算法
启发式速度规划的粗略结果只能提供位置,缺乏控制所需要的更高维信息,不适合控制模块直接使用。产生的结果需要进一步的平滑才能满足舒适度要求。我们进一步做平滑处理的方法使用的是分段常加加速度算法,其主要思想类似于前面介绍的路径优化算法,在给定趋近启发式速度规划结果的情况下,调整启发式速度规划,提高速度分配的平滑性。
分段加加速度算法
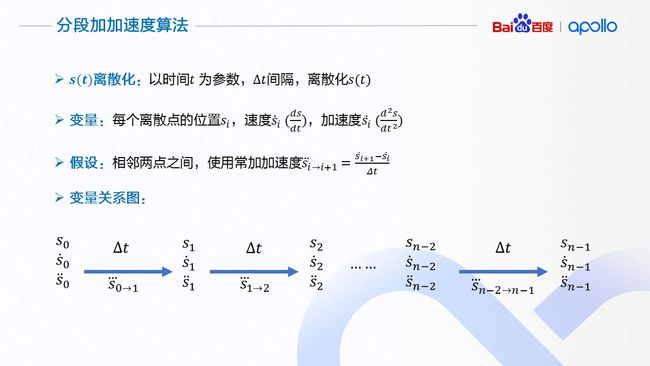
下面我们具体介绍应用在速度平滑上的分段加加速度算法。由于与前面的路径上使用的算法类似,相似的地方就不再赘述。该算法以时间作为离散参数(可以使用启发式算法使用的时间间隔),以每个离散点的位置,速度,加速度作为优化变量,并且假设相邻两点之间,是一个由相邻加速度变量差分得到的加加速度。
在优化函数的设置上,与前面算法相似的地方是惩罚加速度与加加速度的以获得舒适的乘坐体验。不同的一个优化目标是希望位置变量与启发式规划所得到的位置信息尽可能贴近。启发式规划所得到的位置信息蕴含了根据路径几何形状、道路限速等等所做出的计算,这些计算绑定在相应的位置上,所以优化之后的轨迹需要贴近于相应的启发式结果才能体现启发式规划所做的选择。
算法评价与改进
大家可能有的一个问题是,在速度规划的时候,为什么分成启发式的速度规划与分段加加速度算法结合的形式?为何不直接使用加加速度算法进行求解?主要的问题在于在速度规划的时候,我们进行离散的维度、时间,也是我们优化目标的一部分。位置与时间同为优化变量,与位置相关的限制条件, 比如路径曲率,道路限速信息等等,会影响到达位置的时间;而时间的变化又会引起优化速度的变化,进而导致位置发生变化。这就导致了一种变量间耦合变化的情况。启发式速度规划使用粗略的方法,近似解决了位置s决定的限制条件与时间t相互耦合的问题,使时间成为了常量。
但是,这样做也有很明显的不利影响,启发式速度规划的粒度影响了搜索的质量,在搜索过程不够准确,不能反映车辆的动态变化。平滑时单纯贴近启发式速度规划,速度规划并非最优。