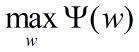《统计学习方法》算法学习笔记五 之 逻辑斯谛回归与最大熵模型
逻辑斯谛回归与最大熵模型
总述
逻辑斯谛回归是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则,将其推广到分类问题得到最大熵模型。逻辑斯谛回归与最大熵模型都属于对数模型。
逻辑斯谛回归模型
1.1 逻辑斯谛分布
逻辑斯谛分布:设 X X X是连续随机变量, X X X服从逻辑斯谛分布是指 X X X具有下列分布函数和密度函数:
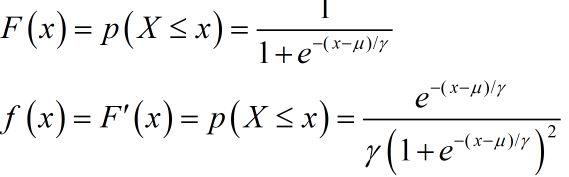
式中, μ \mu μ为未知参数, σ > 0 \sigma>0 σ>0为形状参数。

分布函数在中心附近增长速度较快,在两端增长速度较慢。形状参数 σ \sigma σ的值越小,曲线在中心附近增长越快。
1.2 二项逻辑斯谛回归模型
二项逻辑斯谛回归模型是一种分类模型,由条件概率分布 p ( Y ∣ X ) p(Y|X) p(Y∣X)表示,形式为参数化的逻辑斯谛分布。这里,随机变量 X X X取为实数,随机变量 Y Y Y取为0或1,通过监督学习的方法来估计模型参数。
逻辑斯谛回归模型:二项逻辑斯谛回归模型是如下的条件概率分布:
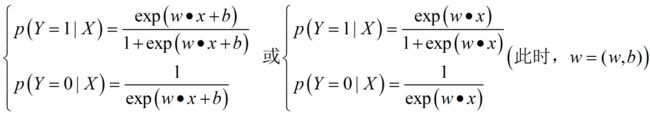
逻辑斯谛回归比较两个条件概率值的大小,将实例 x x x分到概率值较大的一类。
从事件几率的角度看(几率指该事件发生的概率与不发生的概率的比值),如果事件发生的概率是 p p p,那么该事件的几率是 p / ( 1 − p ) p/(1-p) p/(1−p),该事件的对数几率或logit函数是:
l o g i t ( p ) = l o g ( p / ( 1 − p ) ) logit(p)=log(p/(1-p)) logit(p)=log(p/(1−p))对逻辑斯谛回归而言,有
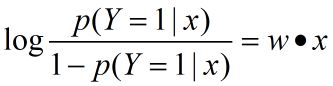
由此可见,在逻辑斯谛回归模型中,输出 Y = 1 Y=1 Y=1的对数几率是输入 x x x的线性函数。
从分类角度看,考虑对输入 x x x进行分类的线性函数 w ∗ x w*x w∗x,其值域为实数域,这里 x ∈ R n + 1 , w 属 于 R n + 1 x∈R^n+1,w属于R^n+1 x∈Rn+1,w属于Rn+1。通过逻辑斯谛回归模型定义式可以将线性函数 w ∗ x w*x w∗x转化为概率:
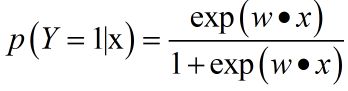
线性函数的值越接近正无穷,概率值越接近1;线性值越接近负无穷,概率值越接近0。
1.3 模型参数估计
逻辑斯谛回归模型学习时,对于给定的训练数据集
T = T= T={ ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) , (x_1,y_1), (x_2,y_2),..., (x_n,y_n), (x1,y1),(x2,y2),...,(xn,yn),}
其中, x i 属 于 R n , y i ∈ x_i属于R^n, y_i∈ xi属于Rn,yi∈{0,1}。可以应用极大似然估计法训练估计模型参数,从而得到逻辑斯谛回归模型。
设: p ( Y = 1 ∣ x ) = π ( x ) p(Y=1|x)=π(x) p(Y=1∣x)=π(x), p ( Y = 0 x ) = 1 − π ( x ) p(Y=0x)=1-π(x) p(Y=0x)=1−π(x)
似然函数为
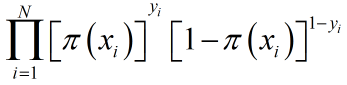
对数似然函数为
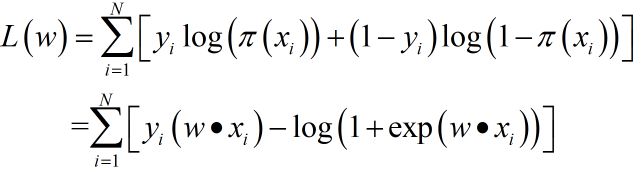
对 L ( w ) L(w) L(w)求极大值,得到 w w w的估计值。问题变成了以对数似然函数为目标函数的最优化问题,通常采用梯度下降或拟牛顿法求解。
1.4 多项逻辑斯谛回归
假设离散型随机变量 Y Y Y的取值集合为{ 1 , 2 , . . . , K 1,2,...,K 1,2,...,K},则多项逻辑斯谛回归模型是
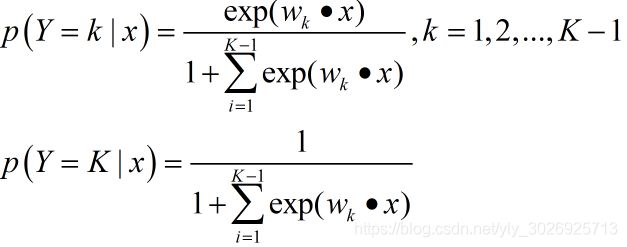
2 最大熵模型
2.1 最大熵原理
最大熵原理是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
假设离散随机变量 X X X的概率分布是 p ( X ) p(X) p(X),则其熵是
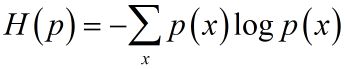 熵满足下列不等式
熵满足下列不等式
0 ≤ H ( p ) ≤ l o g ( x ) 0≤H(p)≤log(x) 0≤H(p)≤log(x)
式中, ∣ X ∣ |X| ∣X∣是 X X X的取值个数,当且仅当 X X X的分布是均匀分布时右边的等号成立。即当 X X X服从均匀分布时,熵最大。
在没有更多信息的情况下,那些不确定的部分都是“等可能的”,最大熵原理通过熵的最大化表示等可能性。
2.2 最大熵模型的定义
假设分类模型是一个条件概率分布 p ( Y ∣ X ) p(Y|X) p(Y∣X),给定一个训练数据集 T = T= T={ ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) (x_1,y_1), (x_2,y_2), ..., (x_N,y_N) (x1,y1),(x2,y2),...,(xN,yN)}。学习的目标是用最大熵原理选择最好的分类模型。
考虑模型应满足的约束条件。给定训练数据集,可以确定联合分布 p ( X , Y ) p(X,Y) p(X,Y)的经验分布和边缘分布 p ( X ) p(X) p(X)的经验分布,分别以如下式子表述:
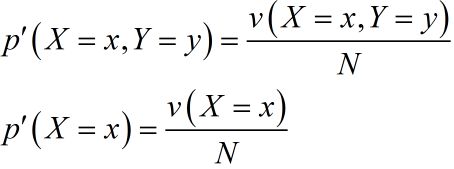
其中, v ( X = x , Y = y ) v(X=x,Y=y) v(X=x,Y=y)表示训练数据样本 ( x , y ) (x,y) (x,y)出现的频数, v ( X = x ) v(X=x) v(X=x)表示训练数据中输入 x x x出现的频数, N N N表示训练样本容量。
用特征函数 f ( x , y ) f(x,y) f(x,y)描述输入 x x x和输出 y y y之间的某一个事实。其定义是

特征函数 f ( x , y ) f(x,y) f(x,y)关于联合分布的经验分布的期望值,用下式表示:
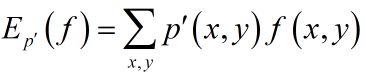
特征函数 f ( x , y ) f(x,y) f(x,y)关于模型 p ( Y ∣ X ) p(Y|X) p(Y∣X)与边缘分布的经验分布的期望值,用下式表示:
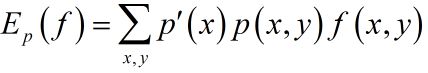
如果模型能够获得训练数据中的信息,则将这两个期望值相等作为模型学习的约束条件,即
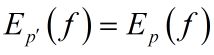 假如有 n n n个特征函数 f i ( x , y ) , i = 1 , 2 , . . . , n f_i(x,y), i=1,2,...,n fi(x,y),i=1,2,...,n,那么就有 n n n个约束条件。
假如有 n n n个特征函数 f i ( x , y ) , i = 1 , 2 , . . . , n f_i(x,y), i=1,2,...,n fi(x,y),i=1,2,...,n,那么就有 n n n个约束条件。
最大熵模型:假设满足所有约束条件的模型集合为
![]()
定义在条件概率分布 p ( Y ∣ X ) p(Y|X) p(Y∣X)上的条件熵为
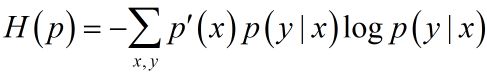
则模型集合 C C C中条件熵 H ( p ) H(p) H(p)最大的模型成为最大熵模型,式中的对数为自然对数。
2.3 最大熵模型的学习
最大熵模型的学习过程就是求解最大熵模型的过程,可以形式化为约束最优化问题。
对于给定的训练数据集 T = T= T={ ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) (x_1,y_1),(x_2,y_2),...,(x_N,y_N) (x1,y1),(x2,y2),...,(xN,yN)}以及特征函数 f i ( x , y ) , i = 1 , 2 , . . . , n f_i(x,y),i=1,2,...,n fi(x,y),i=1,2,...,n,最大熵的学习等价于约束最优化问题:
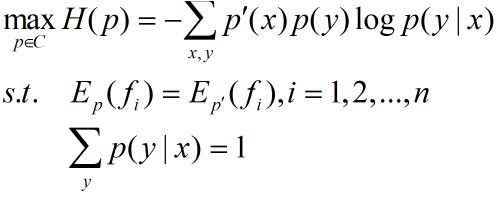
将最大值问题改写为等价的求最小值问题
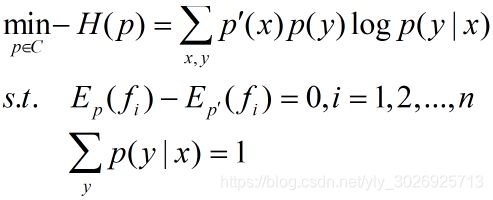
将约束最优化的原始问题转化为无约束最优化的对偶问题,通过求解对偶问题求解原始问题。
首先,引入拉格朗日乘子 w 0 , w 1 , . . . , w n w_0,w_1,...,w_n w0,w1,...,wn,定义拉格朗日函数 L ( p , w ) L(p,w) L(p,w):
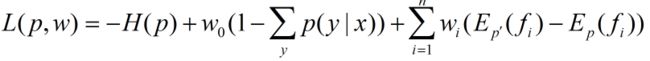
最优化原始问题为
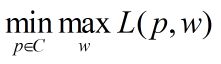
对偶问题为
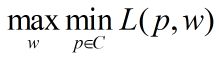
由于拉格朗日函数 L ( p , w ) L(p,w) L(p,w)是 p p p的凸函数,原始问题的解与对偶问题的解是等价的。
其次,求解对偶问题内部的极小化问题
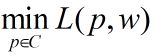
上式是 w w w的函数,记作
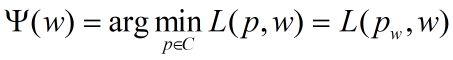
其解记作
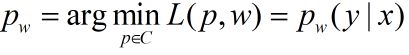
具体地,求 L ( p , w ) L(p,w) L(p,w)的偏导数,并令偏导数为0,结合p’(x)>0和条件概率和为1,得到:
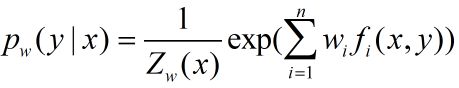
其中
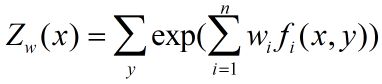
Z w ( x ) Z_w(x) Zw(x)称为规范化因子, f i ( x , y ) f_i(x,y) fi(x,y)是特征函数, p w = p w ( y ∣ x ) p_w=p_w(y|x) pw=pw(y∣x)就是最大熵模型。
最后,求解对偶问题外部的极大化问题
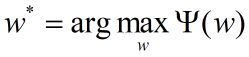
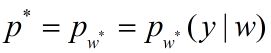 就是学习到的最优化模型(最大熵模型)。
就是学习到的最优化模型(最大熵模型)。
步骤:(1)将原始问题转化为对偶问题;
(2)引进拉格朗日乘子,定义对偶问题的拉格朗日函数;
(3)求解对偶最优化问题
1)求解 L ( p , w ) L(p,w) L(p,w)关于 p p p的极小化问题;
2)求解 L ( p w , w ) L(p_w,w) L(pw,w)关于 w w w的极大化问题。
2.4 极大似然估计
最大熵模型学习中的对偶函数最大化等价于最大熵模型的极大似然估计。这样,最大熵模型的学习问题就转化为具体求解对数似然函数极大化或对偶函数极大化问题。
最大熵模型更为一般的形式是
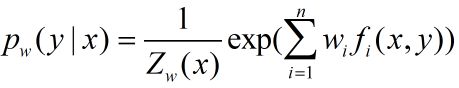
其中
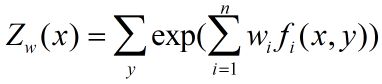
这里, x ∈ R n x∈R^n x∈Rn为输入, y ∈ y∈ y∈{ 1 , 2 , . . . , K 1,2,...,K 1,2,...,K}为输出, w ∈ R n w∈R^n w∈Rn为极值向量, f i ( x , y ) , i = 1 , 2 , . . . , n f_i(x,y),i=1,2,...,n fi(x,y),i=1,2,...,n为任意实值特征向量。
最大熵模型与逻辑斯谛回归模型有类似的形式,他们又称为对数线性模型。模型学习就是在给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计。
3 模型学习的最优化算法
逻辑斯谛回归模型、最大熵模型学习归结为以似然函数为目标的最优化问题。通常通过迭代算法求解。
3.1 改进的迭代尺度法
最大熵模型的对数似然函数为
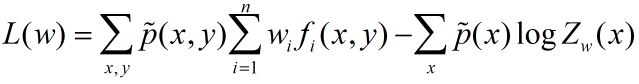 目标是通过极大似然估计学习模型参数,即求对数似然函数的极大值 w ∗ w^* w∗。
目标是通过极大似然估计学习模型参数,即求对数似然函数的极大值 w ∗ w^* w∗。
改进的迭代尺度法(IIS)的想法是:假设最大熵模型当前的参数向量是 w = ( w 1 , w 2 , . . . , w n ) T w=(w_1,w_2,...,w_n)^T w=(w1,w2,...,wn)T,我们希望找到一个新的参数向量 w + δ = ( w 1 + δ 1 , w 2 + δ 2 , . . . , w n + δ n ) T w+\delta=(w_1+\delta_1,w_2+\delta_2,...,w_n+\delta_n)^T w+δ=(w1+δ1,w2+δ2,...,wn+δn)T,使得模型的对数似然函数值增大。若有这样一种参数向量更新方法: w → w + δ w→w+\delta w→w+δ,就可以重复使用这一方法,直到找到对数似然函数的最大值。
对于给定的经验分布 p ~ ( x , y ) \tilde{p}(x,y) p~(x,y),模型参数从 w w w到 w + δ w+\delta w+δ,对数似然函数的该变量是
L ( w + δ ) − L ( w ) ≥ A ( δ , w ) L(w+\delta)-L(w)≥A(\delta,w) L(w+δ)−L(w)≥A(δ,w)如果能够找到合适的 δ \delta δ使得下界 A ( δ , w ) A(\delta,w) A(δ,w)提高,那么对数似然函数也会提高。IIS试图一次只优化其中一个变量 δ i \delta_i δi(因为 A ( δ , w ) A(\delta,w) A(δ,w)中的 δ \delta δ是一个向量),而固定其他变量 δ j , i ≠ j \delta_j,i≠j δj,i=j。IIS进一步降低下界 A ( δ , w ) A(\delta,w) A(δ,w)来达到这一目的。具体的,引进一个量 f ∗ ( x , y ) f^*(x,y) f∗(x,y),
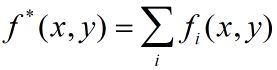
f ∗ ( x , y ) f^*(x,y) f∗(x,y)表示所有特征 ( x , y ) (x,y) (x,y)出现的次数,则有
L ( w + δ ) − L ( w ) ≥ B ( δ ∣ w ) L(w+\delta)-L(w)≥B(\delta|w) L(w+δ)−L(w)≥B(δ∣w)
B ( δ ∣ w ) B(\delta|w) B(δ∣w)是对数似然函数该变量的一个新的下界,求 B ( δ ∣ w ) B(\delta|w) B(δ∣w)对 δ i \delta_i δi的偏导数,并令偏导数为0,即可求出 δ \delta δ。
算法:改进迭代尺度算法IIS
输入:特征函数 f 1 , f 2 , . . . , f n f_1,f_2,...,f_n f1,f2,...,fn;经验分布 p ~ ( X , Y ) \tilde{p}(X,Y) p~(X,Y);模型 P w ( y ∣ x ) P_w(y|x) Pw(y∣x)
输出:最优参数值 w i ∗ w_i^* wi∗;最优模型 p w ∗ p_w^* pw∗
(1)对所有 i ∈ i∈ i∈{ 1 , 2 , . . . , n 1,2,...,n 1,2,...,n},取初值 w i = 0 w_i=0 wi=0
(2)对每一 i ∈ i∈ i∈{1,2,…,n}:
a)令 δ i \delta_i δi是方程
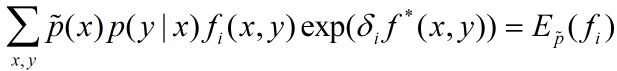
的解,这里
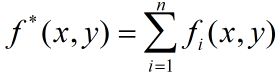
b)更新 w i w_i wi值:
![]() (3)如果不是所有 w i w_i wi都收敛,重复步(2)。
(3)如果不是所有 w i w_i wi都收敛,重复步(2)。
这一算法关键的一步是求解a)中的 δ i \delta_i δi。如果 f ∗ ( x , y ) f^*(x,y) f∗(x,y)是常数,即任何 x , y x,y x,y,有 f ∗ ( x , y ) = M f^*(x,y)=M f∗(x,y)=M,那么 δ i \delta_i δi可以显示的表示为
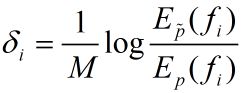
如果 f ∗ ( x , y ) f^*(x,y) f∗(x,y)不是常数,则必须通过数值计算求得 δ i \delta_i δi。牛顿法通过迭代求得 δ i ∗ \delta_i^* δi∗的迭代公式是
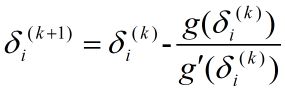
3.2 拟牛顿法
目标函数
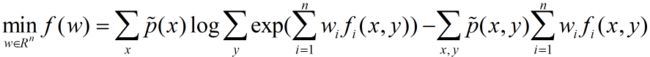 梯度:
梯度:
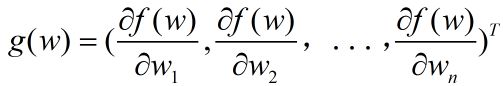
其中,
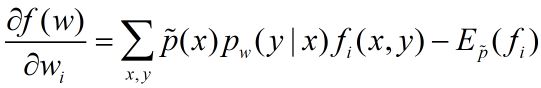
算法:最大熵模型学习的BFGS算法
输入:特征函数 f 1 , f 2 , . . . , f n f_1,f_2,...,f_n f1,f2,...,fn;经验分布 p ~ ( x , y ) \tilde{p}(x,y) p~(x,y);目标函数 f ( w ) f(w) f(w);梯度 g ( w ) = ∇ f ( w ) g(w)=\nabla f(w) g(w)=∇f(w);精度要求 ϵ \epsilon ϵ
输出:最优参数值 w ∗ w^* w∗;最优模型 p w ∗ ( y ∣ x ) p_w^*(y|x) pw∗(y∣x)
(1)选定初始点 w 0 w^0 w0,取 B 0 B_0 B0为正定对称矩阵,置 k = 0 k=0 k=0;
(2)计算 g k = g ( w k ) g_k=g(w^k) gk=g(wk),若|| g k g_k gk||< ϵ \epsilon ϵ,则停止计算,得 w ∗ = w k w^*=w^k w∗=wk;否则转(3);
(3)由 B k p k = − g k B_kp_k=-g_k Bkpk=−gk求出 p k p_k pk;
(4)一维搜索,求 λ k \lambda_k λk使得
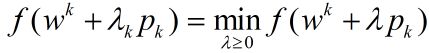
(5)置 w k + 1 = w k + λ k p k w^k+1=w^k+\lambda_kp_k wk+1=wk+λkpk
(6)计算 g k + 1 = g ( w k + 1 ) g_k+1=g(w^k+1) gk+1=g(wk+1),若|| g k + 1 < ϵ g_k+1<\epsilon gk+1<ϵ||,则停止计算,得 w ∗ = w k + 1 w^*=w^k+1 w∗=wk+1;否则,按下式求出 B k + 1 B_k+1 Bk+1:
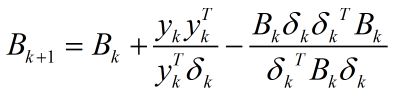 (7)值 k = k + 1 k=k+1 k=k+1,转(3)。
(7)值 k = k + 1 k=k+1 k=k+1,转(3)。