Batch Normalize的几点说明

前言

　　前面也讲过部分Batch Normalize的内容，单独拿出来成文，是因为感觉这方法非常赞，加快训练速度十几倍不等，模型越复杂越受益。
　　一句话总结BN：对每层输入加同分布约束，再加参数线性变换学习其表达能力。

BN解决的问题

　　Problem :: Internal Covariate Shift
　　神经网络训练的难题之一，在前层参数变化时，每层的输入分布也随之变化。这就造成了当层的训练困难，老是变来变去，还能不能好好地玩耍啊~通常地解决思路是使用很小的学习率，并且小心地初始化。
　　Batch Normalize的基本思想是，将每层的输入做std-normalize， y=x−x¯var(x)√ y = x − x ¯ v a r ( x ) ，使得变换后，是 N(0 1) N ( 0   1 ) 高斯分布。

疑问解答

1）Batch Normalize是怎么做的？

　　假设输入m-size的batch样本 x x ，对其中的所有特征都做如下处理：

{x^=x−x¯¯¯var(x)√BN(x)=γx^+βstd⋅normalizescale⋅shift { x ^ = x − x ¯ v a r ( x ) s t d · n o r m a l i z e B N ( x ) = γ x ^ + β s c a l e · s h i f t

　　其中 x¯¯¯=1m∑mi=1xi x ¯ = 1 m ∑ i = 1 m x i ； var(x)=1m∑mi=1(xi−x¯¯¯)2 v a r ( x ) = 1 m ∑ i = 1 m ( x i − x ¯ ) 2

2）单纯地std-normalize能行么？

　　只是将输入约束到同分布下，岂不是所有层的输入都一样了，那还学个毛线啊。在normalize上，Sergey更向前走了一步，一不做二不休，干脆再搞它俩参数 γ γ 和 β β ，将输入恢复出来，通过不断学习调整这两个参数，使得重构输入的能力也能被搞定。

3）梯度消失的现象在带有BN的网络结构里还存在么？

　　误差后传，传递的是误差项 ∗ ∗ 导数项 ∗ ∗ 其他项；传递的动作是链式法则的体现。随着传递路径越长，越容易出现为0的现象。
　　原因1： sigmoid激活函数，自身带有的饱和域（导数近似为0）。
　　原因2： 串联网络本身的参数累乘所带来的梯度消失问题没有解决掉。
　　ReLU激活函数，只是解决了由于激活函数的饱和域（导数近似0）所带来的的梯度消失问题。
　　BN方法，会将训练早期的数据约束到[-1,+1]范围内，避开了饱和区域，也能解决饱和域带来的梯度消失问题。

4）BN在网络中，放到哪里适合？

　　在非卷积网络中，通常是放到激活函数前面，处理之后做激活函数输入： σ(BN(wx)) σ ( B N ( w x ) ) 。
　　notice：由于 BN(wx+b)=BN(wx) B N ( w x + b ) = B N ( w x ) ，会将bias去掉，后面的 β β 起到类似bias的作用。
　　在卷积网络中，则要服从卷积的特性。利用固定filter-blank抽取某一特征feature-map，相当于每个f-map是一个抽取之后的特征（是个整体），那么对只需要对feature-map加统一的 γ γ 和 β β 即可，同样放到激活函数前。详细如下图。

5）如何解释 BN使得网络更稳定的特性

　　假设权重参数 w w 变为 aw a w ，对新旧参数下的 x x 求导如下：

∂BN(awx)∂x=γawvar(awx)−−−−−−−−√=a|a|rwvar(wx)−−−−−−−√=sign(a)∂BN(wx)∂x ∂ B N ( a w x ) ∂ x = γ a w v a r ( a w x ) = a | a | r w v a r ( w x ) = s i g n ( a ) ∂ B N ( w x ) ∂ x

　　发现，虽然参数虽然放缩 a a 倍，但是参数的变化率并没有变化（除了方向），所以参数的放缩对参数变化率无影响。这是很好的特性，表明不会因为参数值的变化，就导致参数变化率飞速增长/缩小，从而使得依赖参数的前向和后向计算值都失控。

6）如何理解 BN对大学习率更友好

　　对于大学习率learning rate, BN是更为友好的。
　　 ⎧⎩⎨⎪⎪BN(wx)=γ(wx)−wx¯¯¯¯¯¯¯var(wx)√+βBN(awx)=γawx−awx¯¯¯¯¯¯¯¯¯¯var(awx)√+β { B N ( w x ) = γ ( w x ) − w x ¯ v a r ( w x ) + β B N ( a w x ) = γ a w x − a w x ¯ v a r ( a w x ) + β ==> ⎧⎩⎨⎪⎪∂BN(wx)∂w=rxvar(wx)√∂BN(awx)∂(aw)=rxvar(awx)√ { ∂ B N ( w x ) ∂ w = r x v a r ( w x ) ∂ B N ( a w x ) ∂ ( a w ) = r x v a r ( a w x )
　　得到：

∂BN(awx)∂(aw)=1|a|∂BN(wx)∂w ∂ B N ( a w x ) ∂ ( a w ) = 1 | a | ∂ B N ( w x ) ∂ w

　　对BN而言，权重变化 wnew=wold−α∂BN∂w=a∗wold w n e w = w o l d − α ∂ B N ∂ w = a ∗ w o l d 时，其中权重的导数，也会按照对应比例 1|a| 1 | a | 变化。
　　若是学习率 α α 较大，训练初始则容易使得 |a|>1 | a | > 1 ，新参数下的梯度反而会压缩到旧参数时的梯度 1|a| 1 | a | 倍，对梯度更新是更安全的，不会无端地放大跑偏。
　　当参数前后两次变化幅度较小，比如a=0.9时，则新梯度是之前梯度的10/9倍，再乘以 α α ，更容易跳出梯度过小而陷入的局部解，或者马鞍部位。
　　更新前后两个梯度和学习率之间互相牵制，是其他方法所不具备的特点。

6）BN怎么计算导数？

　　　　假设其中 ZLj=BN(wLj∗hL−1)=rLj∗∑iwLj,ihL−1i−wLjhL−1¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯var(wLjhL−1)√+βLj Z j L = B N ( w j L ∗ h L − 1 ) = r j L ∗ ∑ i w j , i L h i L − 1 − w j L h L − 1 ¯ v a r ( w j L h L − 1 ) + β j L
　　　　对 wLj,i w j , i L 求导得： ∂Zj∂wLj,i=rLjhL−1ivar(wLjhL−1)√ ∂ Z j ∂ w j , i L = r j L h i L − 1 v a r ( w j L h L − 1 ) ；若无BN，则 ∂Zj∂wLj,i=hL−1i ∂ Z j ∂ w j , i L = h i L − 1
　　　　对 βLj β j L 求导得： ∂BN∂βLj=1 ∂ B N ∂ β j L = 1 。
　　　　对 γLj γ j L 求导得： ∂BN∂γLj=wLjhL−1var(wLjhL−1)√ ∂ B N ∂ γ j L = w j L h L − 1 v a r ( w j L h L − 1 )
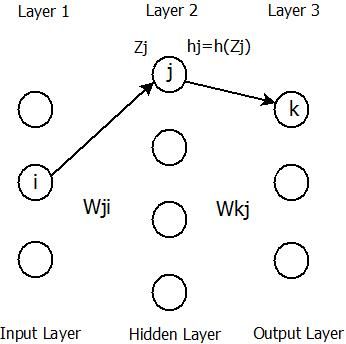
　　在网络中误差后传如下： h=h(z) h = h ( z )
　　 W(L) W ( L ) 记做第 L L 层的权重，连接 L−1 L − 1 和 L L 之间的权重， γ(L)和βL γ ( L ) 和 β L 作为本层学习的标准差向量和偏倚向量，其各自的维度等于本层节点数。
　　a）计算 L L 层的输出误差：
　　　　a.1） δ′(L)={∑δ(L+1)W(L+1)h−y,后层传递过来的δ,本层直接差h−y(最后一层时) δ ′ ( L ) = { ∑ δ ( L + 1 ) W ( L + 1 ) , 后 层 传 递 过 来 的 δ h − y , 本 层 直 接 差 h − y ( 最 后 一 层 时 )
　　　　a.2） δ(L)=δ′(L)∗h′(L)∗r(L)var(W(L)h(L−1))√ δ ( L ) = δ ′ ( L ) ∗ h ′ ( L ) ∗ r ( L ) v a r ( W ( L ) h ( L − 1 ) ) ，乘本层激活导数，再乘BN对w的导数。
　　b）更新 w w ： ΔW(L)=h(L−1)∗δ(L) Δ W ( L ) = h ( L − 1 ) ∗ δ ( L ) 前层输出*本层的 δ δ 。
　　c）更新 β β ： Δβ(L)=δ′(L)∗h′(L) Δ β ( L ) = δ ′ ( L ) ∗ h ′ ( L )
　　d）更新 γ γ ： Δγ(L)=δ′(L)∗h′(L)∗w(L)h(L−1)var(w(L)h(L−1))√ Δ γ ( L ) = δ ′ ( L ) ∗ h ′ ( L ) ∗ w ( L ) h ( L − 1 ) v a r ( w ( L ) h ( L − 1 ) )
　　实际计算时，会在分母的 var v a r 上叠加个随机很小的正数，防止分母为0。最开始初始化时，每对 γ和β γ 和 β 分别都初始化到1和0附近。注意，批量计算均值和方差。
　　补充梯度求导，与paper里面的对比。不是特别明白为什么论文里有对估计参数 u和σ u 和 σ 的求导。
　　训练过程：用batch-GD训练；记录每个 batchB b a t c h B 的 uB和σB u B 和 σ B ，用以最后估计全局的 u和σ u 和 σ 。

9）BN在预测时怎么玩？

　　这个问题的由来：因为预测是单样本依次预测。不存在batch训练的情况，所以预测是与训练不同的，如何利用训练过程及结果参数是个问题。
　　预测时，计算总体的均值和方差是不实际的，也是无法实现的，因为无法采样到所有样本。用总采样来估计总体的均值和方差呢？也是需要大量计算的，在训练过程中的batch下的均值 uB u B 和方差 σB σ B ，可以加以利用来估计总体，如下：　　

{E[x]=E[uB]=1K∑KB=1uBVar[x]=mm−1E[σB] { E [ x ] = E [ u B ] = 1 K ∑ B = 1 K u B V a r [ x ] = m m − 1 E [ σ B ]

　　如上，估计总体的均值和方差，预测时BN不再生效，但是 仍然利用 x^=γx−E[x]Var[x]√+β x ^ = γ x − E [ x ] V a r [ x ] + β 来重构，否则岂不是白学习了重构参数，哈哈。(论文里的那个式子是这个式子稍微变换之后的样子)
　　作者说”Using moving averages instead, we can track the accuracy of a model as it trains”？说的不甚明了，难道是追踪均值和方差的情况。

moving_mean = gamma * moving_mean + (1-gamma)* mean
moving_var  = gamma * moving_var  + (1-gamma)* var

10）几种提高BN效力的方法

　　Sergey友情提示了几个方法，提高BN的效力。
　　增大学习率，学得快还安全；去掉dropout，节省时间；去掉L2正则，但是个人觉得不要去最好，没有理由证明BN能够代替L2；样本集多次shuf，避免同batch总是一样的样本；减少图片变形处理，说的理由不充分；去掉local Response Normalize。

11）怎么理解BN是whiten的简化之后的版本？

　　已有研究说明[2]，针对Internal Covariate Shift问题，将输入做whiten处理，可以收敛地更快。疑问，真有必要whiten么？ICS只是权重变换，影响输出的分布而已，将分布搞得一致不就好了，还用着考虑各个输出变量间的相关关系么，后续层反正也不care变量间的相关性。
　　whiten的处理非常严格：要求去掉各个变量间的相关性；且每个变量的variance=1。
　　whiten定义：将一组随机变量 (X1,X2,....,Xn) ( X 1 , X 2 , . . . . , X n ) 通过 Y=WX Y = W X 变换为 → → (Y1,Y2,...,Ym) ( Y 1 , Y 2 , . . . , Y m ) ，称后者为白噪声，其协方差矩阵为单位对角矩阵，各变量间无相关性( ∃非零系数向量 ∃ 非 零 系 数 向 量 ，使得 aY=0 a Y = 0 成立)， Var[Ym]=1 V a r [ Y m ] = 1 。
　　whiten的求解：假设X有non-singular 协方差矩阵M，and mean=0。
　　方法一： W=M−1/2 W = M − 1 / 2 ZCA白化。
　　方法二：cholesky分解 of M−1 M − 1 。
　　方法三：特征分解 of M M （PCA类方法）。
　　其他相关变换：
　　decorrelation transform：去相关，但是对variance不处理。
　　standard transform： mean=0，variance=1；相关性不处理。
　　corloring transform：白化的逆向处理，将白噪声处理成具有指定协方差矩阵的变换。
　　具体例子见参考3.
　　而BN使用标准化变换，不再考虑相关性，又把全局均值和方差用batch均值和方差来代替，省了大量的计算需要，并且效果还很不错。
　　BN本质，使得同分布；约束范围（量纲归一）。

code example

## model ##
training=True
with tf.variable_scope('layer-1', reuse = tf.AUTO_REUSE):
  y1 = tf.layers.dense(inputs = x, units = 128, use_bias=False, \
                        activation = tf.nn.relu, \
                        kernel_regularizer = regularizer, \
                        bias_regularizer = None)
  y1 = tf.layers.batch_normalization(y1, training= training)
with tf.variable_scope('layer-2', reuse = tf.AUTO_REUSE):
  y2 = tf.layers.dense(inputs = y1, units = 64, use_bias=False, \
                        activation = tf.nn.relu, \
                        kernel_regularizer = regularizer, \
                        bias_regularizer = None)
  y2 = tf.layers.batch_normalization(y2, training= training)
with tf.variable_scope('layer-3', reuse = tf.AUTO_REUSE):
  y3 = tf.layers.dense(inputs = y2, units = 2, use_bias=True, \
                        activation = None, \
                        kernel_regularizer = regularizer, \
                        bias_regularizer = regularizer)

logits     = y3
prob_all   = tf.nn.softmax(logits, 1)

## when training ##
tf.losses.softmax_cross_entropy(onehot_labels=y, logits=logits)
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
## tf.control_dependencies(a): b # a执行后，b才会执行 ##
with tf.control_dependencies(update_ops):
  losses = tf.get_collection('losses')
  total_loss = tf.add_n(losses, name='total_loss')
  grads  = optimizer.compute_gradients(total_losses)
optimizer.apply_gradients(grads, global_step)

## save ## moving_var 不会被存到tf.trainable_variables里面 ##
saver  = tf.train.Saver(tf.global_variables())

## when predict ##
training=False

Reference

1. 《Batch Nomalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
2. 《A Convergence analysis of log-linear training》
3. https://www.projectrhea.org/rhea/index.php/ECE662_Whitening_and_Coloring_Transforms_S14_MH