ReXNet: Diminishing Representational Bottleneck on Convolutional Neural Network 论文学习
Abstract
本文解决了网络中 representational bottleneck 问题,提出了若干设计原则来显著提升模型的表现。作者认为,传统方法设计出来的 representational bottleneck 可能造成模型表现退化。为了深入了解 representational bottleneck,作者研究了上万个随机网络的特征矩阵秩。作者进一步研究了整层的通道配置,设计出更准确的网络结构。基于这些发现,作者提出了一些简单而有效的设计原则,缓和representational bottleneck的副作用。依据这些原则,对基线网络作修改,在ImageNet分类任务上可以明显地提升模型性能。此外,COCO目标检测结果和多个数据集上的迁移学习结果也显示了,减轻representational bottleneck可以提升模型表现。代码和预训练模型位于:https://github.com/clovaai/rexnet。
1. Introduction
构建高效、轻量网络是计算机视觉领域的一个重要课题。以前提出的高效率模型都聚焦在计算效率,试图找到一个廉价的网络设计(如收缩通道维度),在计算成本和准确率上需要做权衡。
本文,作者意图找到一些网络设计原则,在representational bottleneck方法中这些原则是没有的。[46]通过大幅度压缩通道维度,概念上引入了representational bottleneck。作者将一个前馈网络当作无环图,从输入到输出的信息流可能被网络结构阻挡,比如极度的压缩。在语言建模上,[55]首次在softmax层使用了representational bottleneck,Softmax bottleneck。作者证明,有界的矩阵秩会引起representational bottleneck,而在线性softmax上加入额外的非线性来扩展该秩可以解决这个问题。[19,7]也观察到,softmax层的低秩会造成representational bottleneck,降低模型的性能。
本文研究了网络所有层的representational bottleneck。作者首先证明,网络中会有一些层在生成具有判别力的特征方面,编码能力有限,这些层就是representational bottleneck。本文分析了中间特征的矩阵秩,提供了一些简单的原则。而且,作者也进行了一些经验研究,通过随机生成一些网络来探索representational bottleneck,证明了权重矩阵秩和模型的表现直接相关。有了这些证据,作者提出了多项设计原则,提升模型的实际性能:1) 增大层的输入通道维度;2) 选择合适的非线性函数;3) 用多个扩展层来设计网络。作者在ImageNet数据集上,根据这些原则进一步训练了网络,计算每层的矩阵秩。
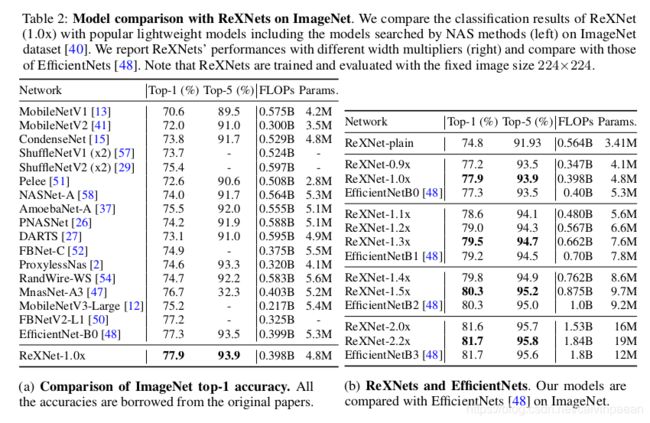
最终,作者提出了新的模型,Rank eXpansion Networks(ReXNets)。只需对基线模型做简单的修改,在ImageNet分类任务上就可以得到明显的提升。该模型超越了那些通过神经结构搜索找到的SOTA模型,它们往往需要巨大的计算资源。因此,本文也鼓励NAS领域的研究人员来采纳本文提出的简单而有效的设计原则,进一步提升表现。在ImageNet分类任务上的性能改进,可以迁移到COCO数据集的目标检测任务和其它高细粒度的分类任务上,证明ReXNets是一个强大的特征提取器。
本文贡献如下:通过数学和实验研究了网络的representational bottleneck问题;新的设计原则,改进网络结构;ImageNet数据集上SOTA的结果,在COCO数据集和不同的细粒度分类任务上迁移学习得到了优异的成绩。
2. On Representational Bottleneck
2.1 Preliminary: Feature Encoding
给定一个深度为 L L L的网络,在 d 0 d_0 d0维度的输入 X 0 ∈ R d 0 × N X_0\in \mathbb{R}^{d_0\times N} X0∈Rd0×N中编码 N N N个特征。用权重矩阵 W i ∈ R d i × d i − 1 W_i \in \mathbb{R}^{d_i \times d_{i-1}} Wi∈Rdi×di−1将特征表示为 X L = σ ( W L ( . . . f 1 ( W 1 W 0 ) ) ) X_L = \sigma(W_L(...f_1 (W_1 W_0))) XL=σ(WL(...f1(W1W0)))。作者将 d i > d i − 1 d_i > d_{i-1} di>di−1的层叫做扩展层,而 d i < d i − 1 d_i < d_{i-1} di<di−1的层叫做收缩层。每个 f i ( ⋅ ) f_i(\cdot) fi(⋅)表示一个point-wise非线性函数,如跟着BN的ReLU激活。 σ ( ⋅ ) \sigma(\cdot) σ(⋅)表示Softmax函数。训练网络时,每一次前向都将输入 X 0 X_0 X0编码为输出 X L X_L XL,最小化 X L X_L XL和标签矩阵 T ∈ R d L × N T\in \mathbb{R}^{d_L \times N} T∈RdL×N的差距。因此,特征如何有效地朝着标签被编码,就关系到这个差距如何被最小化。对于CNN,其形式就要变作 X L = σ ( W L ∗ ( . . . f 1 ( W 1 ∗ X 0 ) ) ) X_L = \sigma(W_L \ast (...f_1(W_1 \ast X_0))) XL=σ(WL∗(...f1(W1∗X0))),其中 ∗ \ast ∗和 W i W_i Wi表示卷积操作和第 i i i个卷积层的权重,卷积核大小是 k i k_i ki。作者通过传统的再排序$ W i X ^ i − 1 W_i \hat X_{i-1} WiX^i−1将每个卷积重写了一遍,其中 W i ∈ R d i × k i 2 d i − 1 W_i \in \mathbb{R}^{d_i \times k_i^2 d_{i-1}} Wi∈Rdi×ki2di−1,重排序后的特征 X ^ i − 1 ∈ R k i 2 d i − 1 × w h N \hat X_{i-1} \in \mathbb{R}^{k_i^2 d_{i-1} \times whN} X^i−1∈Rki2di−1×whN。作者将第 i i i个特征表示为:
X i = { f i ( W i X ^ i − 1 ) i ≤ i < L σ ( W L X ^ L − 1 ) i = L X_i=\left\{ \begin{aligned} f_i(W_i \hat X_{i-1}) & & i\leq i
2.2 Representational bottleneck and matrix rank
Revisiting Softmax bottleneck。作者回顾了softmax bottleneck,一种representational bottleneck,在softmax 层中出现,表示representational bottleneck。从等式1中,交叉熵损失的输出是 log X L = log σ ( W L X L − 1 ) \log X_L = \log \sigma(W_L X_{L-1}) logXL=logσ(WLXL−1),它的秩由 W L X L − 1 W_L X_{L-1} WLXL−1的秩约束,即 min ( d L , d L − 1 ) \min (d_L, d_{L-1}) min(dL,dL−1)。由于输入维度 d L − 1 d_{L-1} dL−1小于输出维度 d L d_L dL,编码特征就无法完全表示所有类别,因为秩的缺陷。为了解决这个问题,[55,19,7] 通过非线性函数缓解了softmax层中秩的缺陷,取得了性能提升。如果我们增大 d L − 1 d_{L-1} dL−1,接近于 d L d_L dL,那么是否也可以减轻representational bottleneck呢?
Diminishing representational bottleneck by layer-wise rank expansion. 作者研究了一些用于图像分类任务的主流网络。这些网络的输出通道(分类器之前)多达1000,将输入通道大小翻倍来下采样,而其它层的输出和输入通道大小相同。作者认为,扩大了通道大小的层(如扩张层)可能会有秩的缺陷问题,造成representational bottleneck。
本文目的是通过扩张权重矩阵 W i W_i Wi的秩,在中间层减轻representational bottleneck问题。给定某层的第 i i i个特征, X i = f i ( W i X i − 1 ) ∈ R d i × w h N X_i = f_i(W_i X_{i-1})\in \mathbb{R}^{d_i\times whN} Xi=fi(WiXi−1)∈Rdi×whN。 r a n k ( X i ) rank(X_i) rank(Xi)受 min ( d i , d i − 1 ) \min(d_i, d_{i-1}) min(di,di−1)约束。 f ( X ) = X ∘ g ( X ) f(X) = X \circ g(X) f(X)=X∘g(X),其中 ∘ \circ ∘表示pointwise乘法。有不等式 r a n k ( f ( X ) ) ≤ r a n k ( X ) ⋅ r a n k ( g ( X ) ) rank(f(X)) \leq rank(X) \cdot rank(g(X)) rank(f(X))≤rank(X)⋅rank(g(X)),特征 X i X_i Xi的秩有如下约束:
r a n k ( X i ) ≤ r a n k ( W i X i − 1 ) ⋅ r a n k ( g i ( W i X i − 1 ) ) rank(X_i)\leq rank(W_i X_{i-1}) \cdot rank(g_i (W_i X_{i-1})) rank(Xi)≤rank(WiXi−1)⋅rank(gi(WiXi−1))
因此,通过增大 r a n k ( W i X i − 1 ) rank(W_i X_{i-1}) rank(WiXi−1)并替换为一个合适的、秩更大的函数 g i g_i gi(如Swish-1或ELU),秩的界可以扩大。当 d i d_i di固定了,如果我们调整特征维度,使 d i − 1 d_{i-1} di−1接近 d i d_i di,上述等式就可以让无界的秩接近特征维度。对于一个由连续的 1 × 1 , 3 × 3 , 1 × 1 1\times 1, 3\times 3, 1\times 1 1×1,3×3,1×1卷积组成的 bottleneck block,作者按照等式2,根据bottleneck block的输入和输出维度大小来扩大秩。
2.3 实验研究
这一部分,作者进行了2个实验研究:基于矩阵秩,层级别的分析和所有层通道配置的研究。首先,作者研究了如何扩大某一层的矩阵秩。本研究目的就是,输入通道大小 d i d_i di和非线性函数 f i f_i fi如何影响矩阵秩。作者基于大量的网络(超过10000个)设计了针对单个层和单个bottleneck的实验,它们的构建模块(如通道大小、非线性激活函数)是随机选取的,再计算它们的秩。其次,对于层级别的研究,作者通过计算矩阵的秩和真实的表现,研究了网络所有的通道配置,来找到一个更优的网络结构。通过固定深度的随机网络,作者在矩阵秩和真实网络性能之间建立了联系。
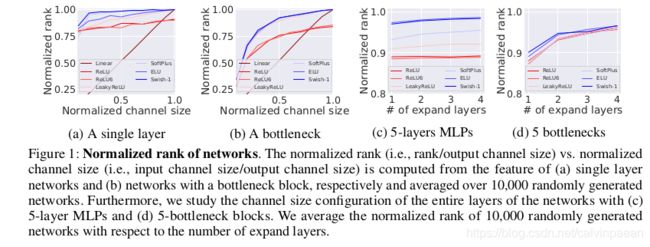
Layer-level rank analysis。为了进行层级别的秩分析,作者生成了一组随机网络,只由单个层构成: f ( W X ) f(WX) f(WX),其中 W ∈ R d o u t × d i n W\in \mathbb{R}^{d_{out}\times d_{in}} W∈Rdout×din, X ∈ R d i n × N X\in \mathbb{R}^{d_{in}\times N} X∈Rdin×N,其中 d o u t d_{out} dout是随机采样得到的, d i n d_{in} din按比例进行设置。然后计算每个网络中特征 r a n k ( f ( W X ) ) / d o u t rank(f(WX))/d_{out} rank(f(WX))/dout归一化的秩。为了研究 f f f,作者采用了广泛使用的非线性函数。对于10000个网络中的每一个网络,针对每个归一化后的通道大小 d i n / d o u t d_{in}/d_{out} din/dout和非线性函数,作者重复实验。通过生成3个连续的随机层(如将 W W W拆分为3个任意大小的矩阵),作者研究了bottleneck block。Bottleneck block的内部扩张比例随机设定。在图1a和1b中,作者报告了归一化后的秩,对于单个层和单个bottleneck block,在10000个网络中取其平均。
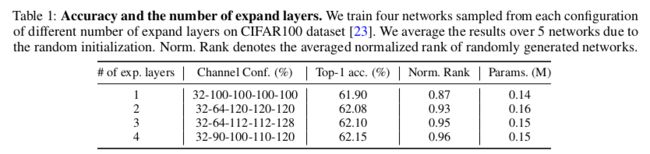
Channel configuration study。作者现在考虑如何设计一个网络,可以设定所有层的通道大小。作者在几个压缩层后用扩展层(即 d o u t > d i n d_{out}>d_{in} dout>din)与 d o u t = d i n d_{out}=d_{in} dout=din的层来随机生成深度为 L L L的网络,因为压缩层会直接降低模型的性能。作者将扩展层的个数随机设置为0到 L − 1 L-1 L−1中一个数。例如,一个网络的扩展层个数为0,所有层有一样的通道大小。对于每个随机生成的网络,重复进行实验,并取归一化后的秩的平均数。结果在图1c和1d中显示。此外,作者报告了选取网络的实际性能,这些网络有5个bottlenecks,stem通道大小是32。在CIFAR100上作者进行了实验,在表1中报告了5个网络的平均准确率。
Observations. 从图1a和1b,作者发现与线性的相比,适当的非线性函数能够很大程度上增大矩阵秩。其次,对于单个层(1a)和bottleneck block(1b)而言,归一化后的输入通道大小 d i n / d o u t d_{in}/d_{out} din/dout与特征秩紧密相关。对于所有层的维度配置,图1c和1d显示,当网络深度固定时,使用更多的扩展层,矩阵秩可以得到提高。而且,该秩的趋势与表1中网络的实际性能匹配。该发现给出了若干设计原则,增大给定网络的秩:1) 扩展某层的输入通道大小 d i n d_{in} din,2) 找到合适的非线性函数;3) 一个网络应该有多个扩展层。
3. Improved Network Architecture
3.1 Where does representational bottleneck occur?
现在我们来思考下representational bottleneck 会出现在网路的哪一层中。所有流行的网络都有着相似的结构,有许多的扩展层,将通道从3-通道输入扩展为 c − c- c−通道的输出预测。首先,下采样模块或层就像一个扩展层。其次,Bottleneck模块和倒转bottleneck模块中的第一层也是一个扩展层。最后,倒数第二层也会增大输出通道的大小。作者认为,在这些扩展层和倒数第二层中,会出现representational bottleneck。
3.2 网络再设计
中间卷积层。作者首先研究了MobileNetV1。按照距离倒数第二层的顺序来改造卷积层。作者改良每一层,通过1) 扩展卷积层的输入通道大小,2) 替换ReLU6。其次,作者改进了MobileNetV2。所有的倒转bottlenecks都按照顺序根据一样的原则来改造。到底将输入通道大小扩展多大是一个开放问题,可以用NAS来处理,出于简洁性,作者建议每个模型都按照本文设计原则来做。对于ResNet和其变体,在每个bottleneck block的第三个卷积层后没有非线性函数,所以扩展输入通道大小是唯一的解药。
倒数第二层。网络结构在倒数第二个卷积层的输出通道大小相对较大。这是为了避免最终分类器的representational bottleneck,但是倒数第二层仍然会有这样的问题。作者将倒数第二层的输入通道大小扩大,替换了ReLU6。
ReXNets。作者现在提出了模型 Rank eXpansion Networks(ReXNets)。作者将根据MobileNetV1和MobileNetV2改进得到的网络分别叫做 ReXNet-plain和ReXNet。该模型证明了,降低representational bottleneck可以提升模型的性能。通道配置的选取刚好满足基线模型的整体的参数量与FLOPs要求,所以利用NAS方法应该可以找到更优的网络结构。
4. Experiments
Pls read paper for more details.