二维树状数组 1：单点修改，区间查询

题目描述

思路

update是从(x,y)处往下更新，sum是求(x,y)到(0, 0)的和
lowbit(x) 表示二进制下x的最低位的1与它后面的0构成的树，那么对于奇数来说就是1

x	1	2	3	4	5	6
二进制	1	10	11	100	101	110
lowbit(x)	1	2	1	4	1	2

假设6x6的数组，更新(2,3)也就是更新标绿的表格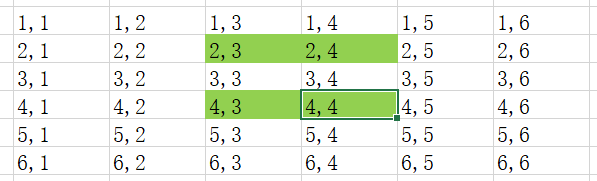

求sum(5, 3)的值就是求标蓝表格的和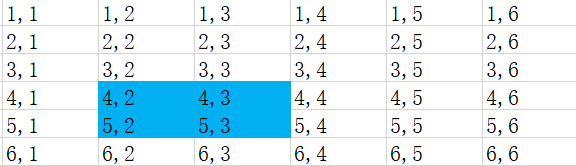

代码

#include 
#include 

int n, m;
long long arr[5005][5005];
int lowbit[5005];
void update(int x, int y, int z) {
    while (x <= n) {
        int j = y;
        while (j <= m) {
            arr[x][j] += z;
            j += lowbit[j];
        }
        x += lowbit[x];
    }
}
long long sum(int x, int y) {
    long long res = 0;
    while (x) {
        int j = y;
        while (j) {
            res += arr[x][j];
            j -= lowbit[j];
        }
        x -= lowbit[x];
    }
    return res;
}
int main() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i < 5005; ++i) lowbit[i] = i & (-i);
    int a, b, c, d, e;
    while (scanf("%d", &a) != EOF) {
        if (a == 1) {
            scanf("%d %d %d", &b, &c, &d);
            update(b, c, d);
        } else {
            scanf("%d %d %d %d", &b, &c, &d, &e);
            printf("%lld\n", sum(d, e) - sum(b - 1, e) - sum(d, c - 1) + sum(b - 1, c - 1));
        }
    }
    return 0;
}

转载于:https://www.cnblogs.com/liuzz-20180701/p/11489755.html