笔试题的思考：移动最少硬币让金字塔上下倒过来

大家找工作笔试的时候经常要做笔试题，除了专业性的题目，还有一个很重要的就是行测题，这也是考验我们的综合逻辑思维能力。

其中有一道关于硬币金字塔的笔试题：

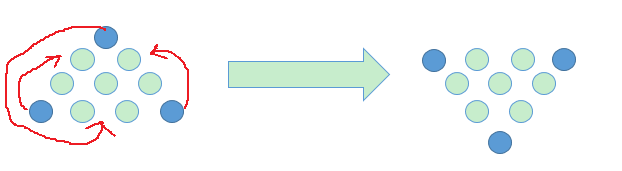
用硬币摆成金字塔，要移动尽可能少的硬币让金字塔上下倒过来，对于 4 层金字塔只要移动图中 3 个蓝色的硬币即可。

问对于 6 层金字塔，要把它倒过来最少需要移动多少枚硬币？

首先这是一个一般性的题目，肯定是有通解的，下面我就来一步一步地阐述自己的思考以及最终的解决方案。

对于最简单的 1 层金字塔，也就是只有一个硬币，这个本身就是上下倒过来的，不需要移动硬币；

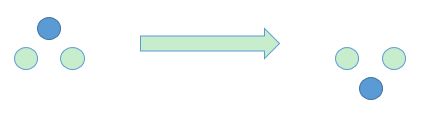
对于 2 层金字塔，共有 3 个硬币，这也很简单，只需要将上面的一个硬币移动到最下面即可；

对于 3 层金字塔，共有 6 个硬币，将最下面一层左右两侧各一个硬币移动到最上面一层左右两侧即可；

对于 4 层金字塔，共有 10 个硬币，具体参考上面题目中的图。

这个时候大家能看到具体的硬币移动方法了吗？

其实我们要做的是先看最后一层，对于 1 层和 2 层金字塔最后一层的硬币不需要移动，对于 3 层和 4 层金字塔需要把最后一层左右两侧各 1 个硬币往上移动。最后一层的硬币 移动后再看还剩余多少硬币，若最后一层剩余的硬币个数为 1，则不需要再移动硬币了；若最后一层剩余的硬币个数为 2，则需要将最上面的一个硬币移动到最后一层下面。

当然，上面的分析只是针对简单的 1~4 层金字塔来说的，但却是下面要解决多层金字塔的重要突破口，至少我们知道大体的思路就是先将最后一层左右两侧的硬币往上移动，再将最上面的硬币往下移动。

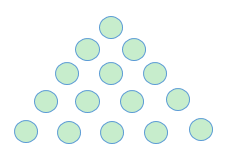
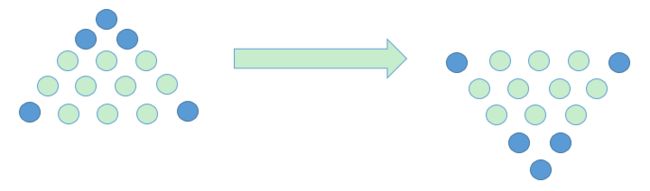
我们再来看一下 5 层金字塔，共有 15 个硬币：

此时我们需要考虑更深一层的问题，最后一层也就是第 5 层有 5 个硬币，按照上面总结的我们先将第 5 层左右两侧的硬币往上移动，但我们可以分别移动左右两侧各 0 个、1 个或 2 个：

• 如果最后一层两侧各移动 0 个，则接下来需要把第 5 层上面所有的硬币全部往下移动（移动了 10 个硬币），总共移动了 10 个硬币；

• 如果最后一层两侧各移动 1 个，则分别它们放到第 3 层的两侧（移动了 2 个硬币），接下来需要把第 3 层上面所有的硬币全部往下移动（移动了 3 个硬币），总共移动了 5 个硬币；
  

• 如果最后一层两侧各移动 2 个，此时需要连着它上一层两侧的各 1 个硬币也要跟着移动，分别将这 6 个硬币中的 2 个放到第 2 层的两侧，还有 4 个放到第 1 层的两侧（移动了 6 个硬币），移动后最后一层上只有 1 个硬币了，所以上面的硬币不需要往下移动了，因此总共移动了 6 个硬币。
  

综合这三种方案，我们很显然会得出第二种移动最少硬币的方案。通过这个分析我们还要明白两点：

• 当最后一层左右两侧各移动 m 个硬币时，要连着它上一层的 m-1 个硬币、上上一层的 m-2 个硬币、……（递减直到最终为 1 个硬币）一起移动。
  
• 最后一层左右两侧各移动 m 个硬币后，最后一层还剩余 n-2*m 个硬币，需要从上面依次往下移动 n-2*m 个硬币、n-2*m-1 个硬币、……（递减直到最终为 1 个硬币）
  

按照上面的方法同样可以分析出 6 层金字塔最少需要移动多少个硬币，此处不再详述，大家可以自己分析一下，下面直接给出各个方案移动硬币数分别为15， 8， 7， 12（移动 12 个硬币是 最后一层左右两侧各移动 3个硬币的情况 ）。

通过分析我们可以得出 6 层金字塔最少需要移动 7 个硬币。但我们总不能一直这样分析吧！对于层数少的可以自己分析，层数太多例如 100 层怎么办？而且一开始我也说了这是有通解的。这个时候很自然的就可以想到靠机器来帮我们做苦力。

对于  n 层金字塔， 编程让机器帮我们计算 每个方案所需要的硬币数目，选择最少的即可。那么具体应该怎么做呢？根据上面的分析，给出方法：

• 首先要清楚总共有多少种方案。显然要根据最后一层左右两侧各移动的硬币数 i 来决定，so easy，最后一层左右两侧各移动的硬币数最多只能是 n / 2 向下取整（记为 lim），则 i 可以取 0、1、2、……、lim，也就是有 lim+1 种方案。
  
• 然后计算每种方案总的移动的硬币数目。这里我们记 sum(x) 函数为 x + (x-1) + (x-2) + ... + 1 的累加和。对于每种方案，根据最后一层左右两侧各移动的硬币数 i 计算出需要从下面往上移动的硬币数为 2*sum(i)，需要从上面往下移动的硬币数为 sum(n-2*m-1)，总的移动硬币数为 total = 2*sum(i) + sum(n-2*m-1)。
  
• 再计算每种方案总的移动的硬币数目的同时，保存移动硬币数最少的方案。

下面给出该方法的 C++ 代码：

#include 
using namespace std;

// sum(x) = x + (x-1) + (x-2) + ... + 1
int sum(int x)
{
	int res = 0;
	for (int i = x; i > 0; --i)
	{
		res += i;
	}
	return res;
}

// 用硬币摆成 n 层的金字塔，移动最少的硬币让金字塔上下倒过来
// 金字塔的第 k 层有 k 个硬币
int coinPyramid(int n, int &m)
{
	// 需要移动第n层的n个硬币中部分，两侧移动个数是对称的，分别为m个，相应其上一层两侧分别移动m-1个...直到两侧分别移动 1 个
	// m 的范围是 0~(int)(n/2)
	// 总的移动硬币个数为： 2 * sum(i) + sum(n - 2 * i -1) = m*(m+1)+(n-2*m)*(n-2*m-1)/2
	int lim = n / 2;
	// total表示对应的总的硬币移动总数，temp为计算移动总数的临时变量，m为最终第n层两侧分别移动的硬币个数
	int total = 0, temp;
	for (int i = 0; i <= lim; ++i)
	{
		temp = 2 * sum(i) + sum(n - 2 * i -1);
		if (total == 0 || temp < total)
		{
			total = temp;
			m = i;
		}
	}
	return total;
}

int main()
{
	int n;
	cout <<  "请输入硬币金字塔的层数： ";
	cin >> n;
	int m = 0;
	while (n != -1)	  // 输入-1时程序结束
	{
		int t = coinPyramid(n, m);
		cout << "最后一层两侧分别移动的硬币数为：" << m
			<< "；最少移动总的硬币数为：" << t << endl;
		cout << "请输入硬币金字塔的层数： ";
		cin >> n;
	}	
	return 0;
}

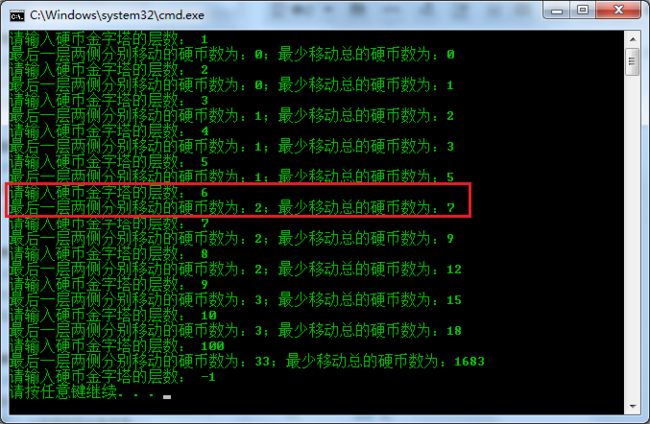
程序运行如下：

接下来我们再从数学的角度来探讨一下这个问题，或许不需要编程我们就能快速得出答案哦！

简单验证一下：

对于 5 层金字塔，x = (5-1) / 3 = 4/3，显然向下取整 1 得到最小值，最小值为 1*2 + (5 - 2*1)*(5 - 2*1 - 1)/2 = 5，这与上面分析的 最后一层左右 两侧各移动 1 个硬币， 总共移动了 5 个硬币是一致的。

同样对于 6 层金字塔， x = (6-1) / 3 = 5/3，显然向上取整 2得到最小值，最小值为 2*3 + (6 - 2*2)*(6 - 2*2 - 1)/2 = 7，同样也是正确 的。

如此一来，对于任意层的金字塔，我们都可以快速求出最少需要移动多少硬币。例如：对于 100 层金字塔，(100-1)/3 = 33 直接取整 33，再带入公式得

33*34 + (100 - 2*33)*(100 - 2*33 - 1)/2 = 1683，在上面的运行程序中可以看到结果是正确的。

当然也可以修改代码，此时就不需要循环了，直接计算比较就行了，修改后的 C++ 代码如下：

#include 
using namespace std;

int sum(int x)
{
	int res = 0;
	for (int i = x; i > 0; --i)
	{
		res += i;
	}
	return res;
}

int coinPyramid(int n, int &m)
{
	double k = (static_cast(n) - 1) / 3;
	if (k - static_cast(k) < static_cast(k) + 1 - k)
	{
		m = static_cast(k);
	}
	else
	{
		m = static_cast(k) + 1;
	}

	int total = 2 * sum(m) + sum(n - 2 * m - 1);
	return total;
}

int main()
{
	int n;
	cout <<  "请输入硬币金字塔的层数： ";
	cin >> n;

	int m = 0;
	while (n != -1)	  // 输入-1时程序结束
	{
		int t = coinPyramid(n, m);
		cout << "最后一层两侧分别移动的硬币数为：" << m
			<< "；最少移动总的硬币数为：" << t << endl;
		cout << "请输入硬币金字塔的层数： ";
		cin >> n;
	}	

	return 0;
}

同样运行程序：

可以看出结果也是一样的。

相信这样一番分析大家应该是有所收获的吧，最重要的是再遇到这样的笔试题就可以直接计算得出结果了，对于层数比较少的记着就能很快写出答案，而不用再花费大量的时间去画图琢磨了。