【周末狂欢赛7】【NOIP模拟赛】七夕祭,齿轮(dfs),天才黑客
文章目录
- T1
- 题目
- 题解
- code
- T2
- 题目
- 题解
- code
- T3
- 题目
- 题解
- code
T1
题目
七夕节因牛郎织女的传说而被扣上了「情人节」的帽子。于是TYVJ今年举办了一次线下七夕祭。Vani同学今年成功邀请到了cl同学陪他来共度七夕,于是他们决定去TYVJ七夕祭游玩。
TYVJ七夕祭和11区的夏祭的形式很像。矩形的祭典会场由N排M列共计N×M个摊点组成。虽然摊点种类繁多,不过cl只对其中的一部分摊点感兴趣,比如章鱼烧、苹果糖、棉花糖、射的屋……什么的。Vani预先联系了七夕祭的负责人zhq,希望能够通过恰当地布置会场,使得各行中cl感兴趣的摊点数一样多,并且各列中cl感兴趣的摊点数也一样多。
不过zhq告诉Vani,摊点已经随意布置完毕了,如果想满足cl的要求,唯一的调整方式就是交换两个相邻的摊点。两个摊点相邻,当且仅当他们处在同一行或者同一列的相邻位置上。由于zhq率领的TYVJ开发小组成功地扭曲了空间,每一行或每一列的第一个位置和最后一个位置也算作相邻。现在Vani想知道他的两个要求最多能满足多少个。在此前提下,至少需要交换多少次摊点。
输入格式
第一行包含三个整数N和M和T。T表示cl对多少个摊点感兴趣。
接下来T行,每行两个整数x, y,表示cl对处在第x行第y列的摊点感兴趣。
输出格式
首先输出一个字符串。如果能满足Vani的全部两个要求,输出both;如果通过调整只能使得各行中cl感兴趣的摊点数一样多,输出row;如果只能使各列中cl感兴趣的摊点数一样多,输出column;如果均不能满足,输出impossible。
如果输出的字符串不是impossible, 接下来输出最小交换次数,与字符串之间用一个空格隔开。
样例
样例输入1
2 3 4
1 3
2 1
2 2
2 3
样例输出1
row 1
样例输入2
3 3 3
1 3
2 2
2 3
样例输出2
both 2
数据范围与提示
对于30% 的数据,N, M≤100。
对于70% 的数据,N, M≤1000。
对于100% 的数据,1≤N, M≤100000,0≤T≤min(NM, 100000),1≤x≤N,1≤y≤M
题解
这道题先初级均分纸牌,后中级糖果传递,然后这题就变成水题了

我们知道如果要满足每一行或者每一列的摊点数一样,感兴趣的摊点数一定能整除行或列
这道题的行与列操作是彼此独立的,接下来以行为例,大家类比列
考虑糖果怎么写的,把这 n n n行,每一行看成一个人,那么一共就有 n n n个人,围成一圈,每个人手上的糖果就是该行感兴趣的摊点数,设平均数 a v e r = T / n aver=T/n aver=T/n,每一个人都会向右边的人传递糖果然后接受左边的人传来的糖果,最后手上均有 a v e r aver aver个,设原本手上就有 p i p_i pi颗糖果, X i X_i Xi表示第 i i i个人给了第 i − 1 i-1 i−1人 X i X_i Xi颗糖,特殊的 X 1 X_1 X1表示第一个人给第 n n n个人,如果值为负则表示 i − 1 i-1 i−1给 i i i
然后就可以写出 n n n个方程
{ p 1 − X 1 + X 2 = a v e r − − > X 2 = a v e r − p 1 + X 1 ( 令 p r e [ i ] = ∑ j = 1 i a v e r − X j ) p 2 − X 2 + X 3 = a v e r − − > X 3 = a v e r − p 2 + X 2 − − > X 3 = a v e r − p 2 + a v e r − p 1 + X 1 = X 1 + p r e [ i ] . . . p n − X n + X 1 = a v e r − − > X n = X 1 + p r e [ n ] \begin{cases} p_1-X_1+X_2=aver-->X_2=aver-p_1+X_1(令pre[i]=\sum_{j=1}^{i}aver-X_j)\\ p_2-X_2+X_3=aver-->X_3=aver-p_2+X_2-->X_3\\ =aver-p_2+aver-p_1+X_1=X_1+pre[i]\\ ...\\ p_n-X_{n}+X_{1}=aver-->X_n=X_1+pre[n]\\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧p1−X1+X2=aver−−>X2=aver−p1+X1(令pre[i]=∑j=1iaver−Xj)p2−X2+X3=aver−−>X3=aver−p2+X2−−>X3=aver−p2+aver−p1+X1=X1+pre[i]...pn−Xn+X1=aver−−>Xn=X1+pre[n]
这里我们翻转 p r e pre pre的定义, p r e [ i ] = ∑ j = 1 i X j − a v e r pre[i]=\sum_{j=1}^iX_j-aver pre[i]=∑j=1iXj−aver
那么最后的答案则是 m i n ( ∣ X 1 ∣ + ∣ X 1 − p r e [ 1 ] ∣ + ∣ X 1 − p r e [ 2 ] ∣ . . . ∣ X 1 − p r e [ n ] ∣ ) min(|X_1|+|X_1-pre[1]|+|X_1-pre[2]|...|X_1-pre[n]|) min(∣X1∣+∣X1−pre[1]∣+∣X1−pre[2]∣...∣X1−pre[n]∣)
注意这个绝对值可以用数轴的含义来表示, ∣ X 1 − Y ∣ |X_1-Y| ∣X1−Y∣表示在数轴上 X 1 X_1 X1与 Y Y Y之间的距离
然后我们就可以把 p r e [ i ] pre[i] pre[i]对应到数轴上面,然后调用初中知识,当 X 1 X_1 X1取之中位数时,距离和最小

code
#include T2
题目
现有一个传动系统,包含了 N N N个组合齿轮和 M M M个链条。每一个链条连接了两个组合齿轮 u u u和 v v v,并提供了一个传动比 x : y x:y x:y 。即如果只考虑这两个组合齿轮,编号为 u u u的齿轮转动 x x x圈,编号为 v v v的齿轮会转动 y y y圈。传动比为正表示若编号为 u u u的齿轮顺时针转动,则编号为 v v v的齿轮也顺时针转动。传动比为负表示若编号为 u u u的齿轮顺时针转动,则编号为 v v v的齿轮会逆时针转动。若不同链条的传动比不相容,则有些齿轮无法转动。我们希望知道,系统中的这 N N N个组合齿轮能否同时转动。
输入格式
有多组数据,第一行给定整数 T T T,表示总的数据组数,之后依次给出 T T T组数据。
每一组数据的第一行给定整数 N N N和 M M M,表示齿轮总数和链条总数。
之后有 M M M行,依次描述了每一个链条,其中每一行给定四个整数 u u u, v v v, x x x 和 y y y,表示只考虑这一组联动关系的情况下,编号为 u u u的齿轮转动 x x x圈,编号为 v v v的齿轮会转动 y y y圈。请注意, x x x为正整数,而 y y y为非零整数,但是 y y y有可能为负数。
输出格式
输出 T T T行,对应每一组数据。首先应该输出标识这是第几组数据,参见样例输出。之后输出判定结果,如果 N N N个组合齿轮可以同时正常运行,则输出 Yes,否则输出 No。
样例
样例输入
2
3 3
1 2 3 5
2 3 5 -7
1 3 3 -7
3 3
1 2 3 5
2 3 5 -7
1 3 3 7
样例输出
Case #1: Yes
Case #2: No
数据范围与提示
对于所有的数据, T ≤ 32 , N ≤ 1000 , M ≤ 10000 , ∣ x ∣ , ∣ y ∣ ≤ 100 T\le 32,N\le 1000,M\le 10000,|x|,|y|\le 100 T≤32,N≤1000,M≤10000,∣x∣,∣y∣≤100
题解
这里其实理解了相容是什么意思就可以了
无非就是每一个齿轮因为我们按的链条有了一定的旋转速度
然后保证这些链条所涉及的齿轮彼此间的旋转速度是永恒的
那么我们就可以用 d f s dfs dfs判断即可:
以单位"1"的旋转速度开始,当 u u u点以单位"1"旋转,那么 v v v点就会以 y x \frac{y}{x} xy速度旋转
当这个齿轮没有被访问过就更新它的旋转速度
反之则判断此时它的旋转速度跟之前的速度是否一致
这道题比较良心不会卡精度
code
#include T3
题目
SD0062 号选手小 Q 同学为了偷到 SDOI7012 的试题,利用高超的黑客技术潜入了 SDOI 出题组的内联网的中央控制系统,然而这个内联网除了配备有中央控制系统,还为内联网中的每条单向网线设定了特殊的通信口令,这里通信口令是一个字符串,不同网线的口令可能不同。这让小 Q 同学感觉有些棘手, 不过这根本难不倒他,很快他就分析出了整个内联网的结构。
内联网中有 n n n个节点(从 1 1 1到 n n n标号)和 m m m条单向网线,中央控制系统在第 1 1 1个节点上,每条网线单向连接内联网中的某两个节点,从 1 1 1号节点出发经过若干条网线总能到达其他任意一个节点。每个节点都可以运行任意的应用程序,应用程序会携带一条通信口令,当且仅当程序的口令与网线的口令相同时,程序才能通过这条网线到达另一端的节点继续运行,并且通过每条网线都需要花费一定的时间。
每个应用程序可以在任意一个节点修改通信口令,修改通信口令花费的时间可以忽略不计,但是为了减小修改量,需要先调用一个子程序来计算当前程序的口令和网线的口令的最长公共前缀(记其长度为 l e n len len),由于获取网线的口令的某个字符会比较耗时,调用一次这个子程序需要花费 l e n len len个单位时间。
除此之外,小 Q 同学还在中央控制系统中发现了一个字典,每条网线的口令都是字典中的某个字符串。具体来说,这个字典是一棵 k k k个节点(从 1 到 k 标号)的有根树,其中根是第 1 1 1个节点,每条边上有一个字符,字符串 S S S在字典中当且仅当存在某个点 u u u使得从根节点出发往下走到 v v v的这条路径上的字符顺次拼接构成 S S S。
现在小 Q 同学在 1 1 1号节点同时开启了 n − 1 n-1 n−1个应用程序,这些应用程序同时运行且互不干扰,每个程序的通信口令都为空,他希望用最短的时间把这些程序分别发送到其他节点上,你需要帮小 Q 同学分别计算出发送到第 i ( = 2 , 3 , . . . n ) i(=2,3,...n) i(=2,3,...n)个节点的程序完成任务的最短时间。

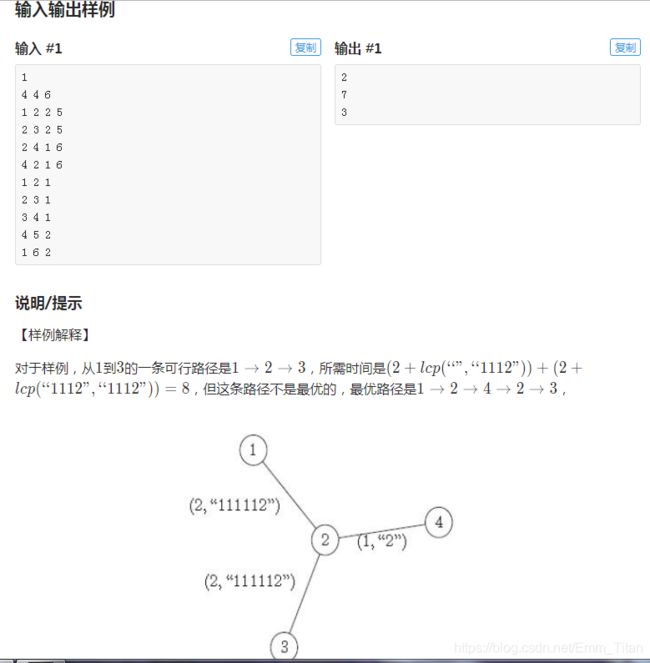

题解
首先我们把一条边拆成四个点,这条边的发起者(出点)和这条边的接受者(入点)以及各自再建一个虚点,彼此之间的权还是以前的边权

建一个源点s,然后向所有入点是1的点建一条边权为0的边
然后枚举每一个点u,将所有形如
跑一次原图对于源点而言的最短路
最后,对于一个点u,枚举所有
但是一个点的入边和出边会有很多,别人都说连出的边数大概是 O ( n 2 ) O(n^2) O(n2)的GG了
所以我们考虑优化建图:
一条边被拆成四个点,两个入点两个出点,分别用来处理前缀和后缀
对于一个点,我们以前缀为例子,后缀与之类似以下略过 :
1.按照每条边对应字符串在Trie树上的dfs序排序,上面是入边,下面是出边
2.上下分别按照顺序连边权为0的有向边(灰色边)
3.考虑到一个性质 l c p ( a 1 , a n ) = m i n i = 1 n − 1 l c p ( a i , a i + 1 ) lcp(a_1,a_n)=min^{n−1}_{i=1}lcp(a_i,a_{i+1}) lcp(a1,an)=mini=1n−1lcp(ai,ai+1)
4.考虑dfs序相邻的两点 x i , x i + 1 x_i,x_{i+1} xi,xi+1(有可能都是入点或出点),计算出 l c p ( x i , x i + 1 ) lcp(x_i,x_{i+1}) lcp(xi,xi+1)
考虑它们的影响范围,显然,我们找到序号最大且小于等于 i i i的入边 c k c_k ck和序号大于等于 i + 1 i+1 i+1的出边 r j r_j rj,连边 < c k , r j >
这样,就可以满足一个序号小的入边到任意一个序号比它大的出边之间的最短路就是它们的lcp值

对于步骤4,其实是一种虚树的思想吧
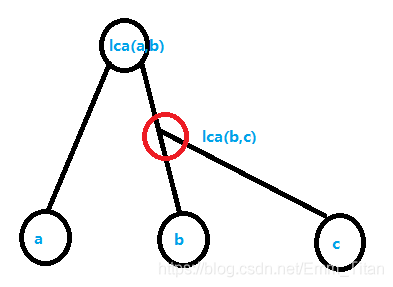
经典的就是为什么按 d f n dfn dfn序排序后两两之间的 l c a lca lca会覆盖任意两个点之间的 l c a lca lca
接下来给出简单证明,假设 a , b , c a,b,c a,b,c是排序后紧挨着的三个点且 d f n a < d f n b < d f n c dfn_a
因此 b b b不可能成为 l c a ( a , b ) lca(a,b) lca(a,b), c c c不可能成为 l c a ( b , c ) , l c a ( a , c ) lca(b,c),lca(a,c) lca(b,c),lca(a,c)
那么会有几种情况呢?
情况1:当 b , c b,c b,c的 l c a lca lca在 a , b a,b a,b的 b − l c a ( a , b ) b-lca(a,b) b−lca(a,b)路径上( c c c可以是 b b b的儿子,是一样的情况),显然 l c a ( a , c ) = l c a ( a , b ) lca(a,c)=lca(a,b) lca(a,c)=lca(a,b)
情况2: l c a ( a , b ) = l c a ( b , c ) lca(a,b)=lca(b,c) lca(a,b)=lca(b,c)那么也很简单 l c a ( a , c ) = l c a ( a , b ) = l c a ( b , c ) lca(a,c)=lca(a,b)=lca(b,c) lca(a,c)=lca(a,b)=lca(b,c)
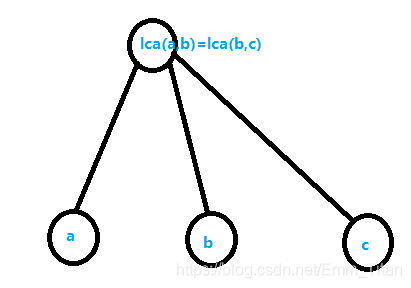
情况3: l c a ( b , c ) lca(b,c) lca(b,c)在 l c a ( a , b ) lca(a,b) lca(a,b)的子树外,那么 l c a ( a , b ) lca(a,b) lca(a,b)一定是 l c a ( b , c ) lca(b,c) lca(b,c)子树内的一点
因此 l c a ( a , c ) = l c a ( b , c ) lca(a,c)=lca(b,c) lca(a,c)=lca(b,c)
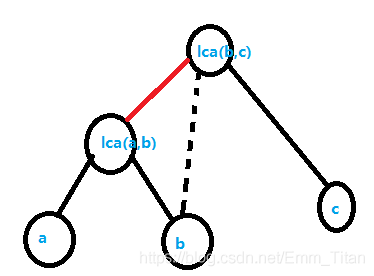
情况4: l c a ( a , c ) lca(a,c) lca(a,c)在 a − l c a ( a , b ) a-lca(a,b) a−lca(a,b)路径上,这个时候好像出了问题别急往下看

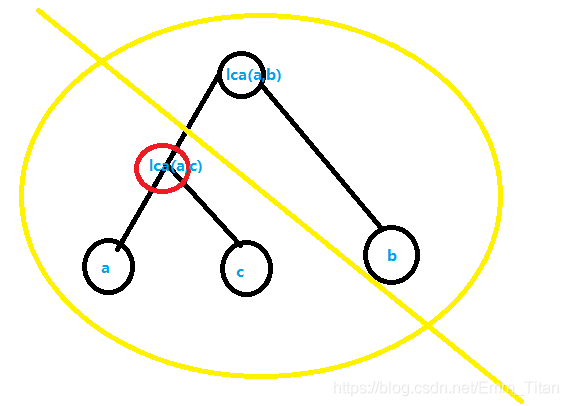
根据 d f n dfn dfn的定义,我们得把 l c a ( a , c ) lca(a,c) lca(a,c)的子树遍历完了才能去 b b b那一边
那么按道理 d f n c < d f n b dfn_c
code
#include