2020牛客寒假算法基础集训营3——B.牛牛的DRB迷宫II【构造 & 二进制】

题目传送门

---

题目描述

牛牛有一个n*m的迷宫，对于迷宫中的每个格子都为’R’,‘D’,'B’三种类型之一，'R’表示处于当前的格子时只能往右边走’D’表示处于当前的格子时只能往下边走，而’B’表示向右向下均可以走。

我们认为迷宫最左上角的坐标为(1,1)，迷宫右下角的坐标为(n,m)，除了每个格子有向右移动以及向下移动的限制之外，你也不能够走出迷宫的边界。

牛牛现在请你设计迷宫，但是要求你设计的迷宫符合他的要求，他要求你设计的迷宫从(1,1)节点移动到(n,m)节点不同的移动序列种类数目 $\equiv k(mod10^9+7)$。

请你构造出符合条件的DRB迷宫，但是要求你输出的迷宫的大小不超过50*50，具体输出格式见输出描述及样例。

如果存在多解你可以构造任意符合条件的迷宫，反之如果无解，请输出一行一个字符串"No solution"。

---

输入描述:

仅一个整数k，你需要构造一个DRB迷宫符合从左上走到右下的方案数 $\equiv k(mod10^9+7)$

---

输出描述:

请你构造出符合条件的DRB迷宫,但是要求你输出的迷宫的大小不超过50*50。

第一行输出n,m两个整数，中间用空格隔开。
接下来n行，每行输出一个大小为m的字符串，字符串只能包含大写字母’D’,‘R’,‘B’。
如果存在多解你可以构造任意符合条件的迷宫，反之如果无解，请输出一行一个字符串"No solution"。

---

输入

25

---

输出

5 5
RBBBR
BBBBB
BBBDB
BDBBB
RBBBB

---

说明

样例为《牛牛的DRB迷宫I》中的样例反过来。

---

备注:

$\equiv$ 为同余等号，意为等式两边在对模数取余后的结果相同。
本题为Special Judge类型，只要符合题目要求的答案均可通过。

---

题解

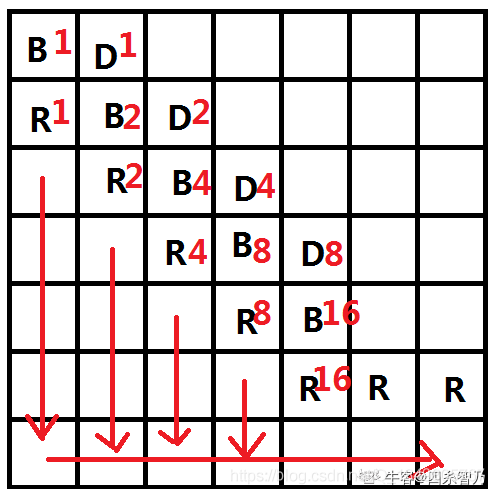
• 可以构造一个 $二进制编码器$，斜对角线上的方案数恰好等于$1，2，4，8，16，32，....$用二进制可以拼出所有的数字，一定可以造出来
  

---

AC-Code

#include 
using namespace std;

char s[30][32];
int main() {
	memset(s, 'R', sizeof(s));
	for (int i = 0; i < 30; i++) s[i][30] = 'D', s[i][31] = '\0';
	for (int i = 0; i <= 28; i++) s[i][i] = 'B';
	int k; while (cin >> k) {
		for (int i = 0; i <= 28; i++) 
			s[i][i + 1] = k & 1 << i ? 'B' : 'D';
		s[29][29] = k & 1 << 29 ? 'B' : 'D';
		cout << 30 << " " << 31 << endl;
		for (int i = 0; i < 30; i++) 
			cout << s[i] << endl;
	}
	return 0;
}