第四章 World Representations
4.4 世界表现(World Representations)
真实地游戏世界并不是由寻路算法所使用的节点和连线所组成。为了让游戏关卡能被寻路使用,需要把地图的几何图形和角色的移动能力转成由节点和连线组成的图结构。
对于每一种寻路世界表现,都是将游戏关卡分割成对应点和连接的链接区域。这些实现方式被称作划分方案(division schemes)。每一个划分方案都依次有三个考虑的重要特性:量化/本地化,生成(generation),有效性(validity)。
量化(Quantization)和本地化(Localization)
因为寻路图比真实的游戏关卡简单,需要一些机制将游戏的位置转化为图中的节点。比如当一个角色需要抵达一个开关的时候,角色和开关的位置需要被转换成图中节点。这个过程被称作量化。
相似的,如果一个角色随着寻路产生的路径移动,需要把路径上的节点转换成游戏中的位置,这被称作本地化。
生成(Generation)
有很多将一个连续的空间分割成寻路使用的区域和连接的方式。这里有一些常用的标准方法。每一个手动或者算法生成。
理想上当然是更希望使用自动生成的技术。然而另一方面,手工技术通常产生最好的结果,能够对任意特定的关卡执行。
最常使用的手工划分方案是狄利克雷域(Dirichlet domain)。最常用的算法技术是瓦片图,可视点法和寻路网格。寻路网格和可视点法通常会扩展通过用户的监督来自动划分。
有效性(Validity)
如果一个计划让一个角色沿着一个连接从节点A移动到节点B,角色需要执行这个移动。这意味着无论角色在节点A的任何位置,他都应该能够到节点B的任何位置。如果在节点A和B附近的量化区域不允许这个移动,则寻路创建了一个无用的计划。
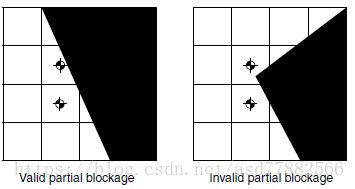
如果两个相连的两个区域,从一个区域的任一点都能到达另一个的任一点,成这个划分方案是有效的。现实中,大部分划分方案不强制有效性。可能有不同的有效等级,如下图示:

第一个问题不大,一个障碍躲避算法可以简单的解决问题。第二个使用同样算法,会中断。使用一个产生第二种图的划分方案是不明智的。不幸的是,分割线很难预测,an easily handled invalidity is only a small change away from being pathological(病态的)
理解每一个划分方案的有效属性是很重要的,至少角色的移动算法可以使用。
4.4.1 瓦片图(Tile Graphs)
基于瓦片的关卡,是由2d等大的二维图像组成,几乎已经从主流游戏中消失。但是远没有死亡。即使严格来说不是由瓦片组成,很多游戏仍然将3d的模型放入网格中。潜在的图像仍然是有规律的网格。
网格可以很容易转换成瓦片图。许多实时策略游戏(RTS)仍然广泛使用瓦片图,很多室外游戏使用基于高度和地形数据的图。
瓦片图关卡将整个世界分割成有规律的正方形,或者区域(通常在一些战争模拟游戏是六边形)。
划分方案
世界中的瓦片代表寻路图中的节点。每一个瓦片都有一组明显的邻居(比如说在矩形网格中是它周围的八个瓦片).节点之间的连接联系它们的邻居。
量化/本地化
我们可以判定世界中的任意一点在哪一个瓦片中,这通常执行的很快。在正方形网格中,我们可以简单的使用角色的x,z坐标决定他在哪个,比如:
tileX = floor(x / tileSize)
tileZ = floor(z / tileSize)同样的,我们可以使用一个节点转换成世界坐标的一个瓦片位置(通常是中心点)。
生成
瓦片图被自动生成。因为它们如此有规律(通常有一样的连接并且很容易量化),可以在运行时生成。瓦片图的一个实现不需要事先对每个节点的连接进行存储。可以在寻路需要时才生成它们。
大部分游戏允许瓦片被阻塞。即图中与阻塞节点无连接,寻路也不会尝试穿过它们。
基于网格可以代表户外的高度场(一个高度值的矩形网格),花费值通常基于坡度。高度场数据被用来生成一个连接的花费,它基于距离和坡度。高度场的每一个例子代表图中的瓦片中心点,花费基于它们的距离和高度差生成。这样下坡花费的更少,上坡花费的更多。
有效性
很多使用基于瓦片布局的游戏,一个瓦片要么完全阻塞要么完全空置。在这种情况下,所有可以连接的节点都是空置的,那么图就可以保证有效。
当一个图的节点部分阻塞,那么图有可能有效,由阻塞的形状决定。下图展示了两种情况:一个部分阻塞没有使图无效,另一个使图变无效:
缺点
基于瓦片的关卡是最容易生成图的一种。游戏里边经常有很多数量的瓦片。一个小的rts关卡可以有成百上千的瓦片。这意味寻路需要工作很久来计划路径。
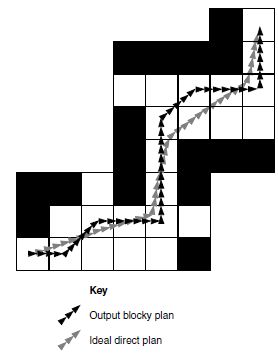
当寻路返回图中的计划路径时,可能会显得块状和不规则,角色按照这种路径移动会显得很奇怪,如下图所示:
在所有的划分方案中都有这种情况,在瓦片图中最明显(之后的路径平滑是一个解决这个问题的一个方式)。
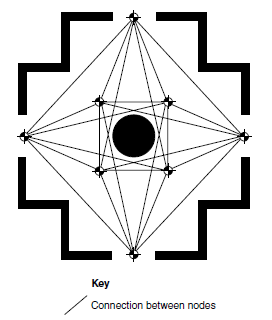
4.4.2 狄利克雷结构域(Dirichlet Domains)
狄利克雷结构域,同样是二维中的沃罗诺伊多边形(Voronoi polygon),是一个由一系列有限源点分割成的区域,每一个区域中的任一点距离该对应源点距离最近。
划分方案
在空间中对应的寻路点被称为特征点,量化则通过将Dirchlet域中的所有位置点映射到节点。为了确定游戏中一个位置对应的寻路点,我们查找最近的特征点。
特征点通常由关卡设计师制定并作为关卡数据的一部分。
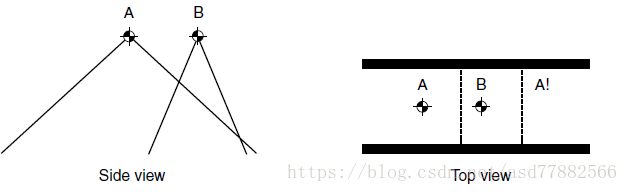
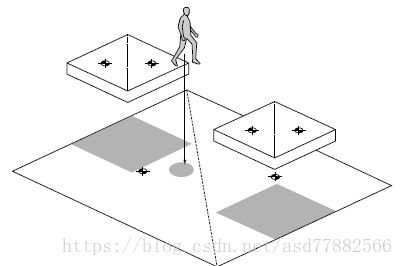
可以将狄利克雷结构域作为从源点起始的椎体,如下图如果从上往下看,每一个椎体的区域属于对应源点,这对于故障排除是一个非常有用的可视化手段。
进一步扩充对每一个点使用不同的衰减函数,在量化步骤一些节点相对来说有更大的引力。这被称为weighted Dirichlet domain:每一个节点都有一个控制它区域大小的权重值。改变权重值相当于改变椎体的坡度,更平缓的椎体有更大的区域。但是需要注意,一旦改变坡度,可能会得到奇怪的效果。
如下图所示,Dirichlet domains是一个通道。可以看到通道的结尾有一个错误的源点:大的椎体(A)超出了B。这会增加调试寻路问题的难度.
如果要手动制定weighted Dirichlet domains,让它们可视化会是一个检查重叠问题的好方法。
相邻的区域放置连接。这些连接的模式可以看到和一个数学结构Voronoi diagrams有很深的联系,被称作德劳内三角化(Delaunay triangulation)。德劳内三角化的边是对应图的连接,顶点是域的特征点。创建一系列点的德劳内三角超出了本书内容,不过可以网上查找到。
大多数开发者并不会为如何选择正确算法所困扰,他们要么让关卡设计者指定连接,要么直接使用光线投射检查连接(点的可见性后文会讲到)。即使使用德劳内三角化,仍然需要检测相邻区域是否联通,比如在连线上有一堵墙。
量化和本地化
位置通过寻找最近的特征点来量化。
寻找最近点是一个很耗时的操作(O(n),n是域的数量),我们可以使用一些空间分割算法(四叉树,八叉树,二元空间划分,多分辨率地图)来只考虑最近点。
节点的位置是域中的特征点坐标(上例中的椎体顶点)。
有效性
Dirichlet domains可能产生复杂的形状。没有方法能够保证从一个区域的一个点到相邻区域的另一个点不会穿过第三个区域。这第三个区域可能已经不可通过或者从寻路中断开,在这种情况下,跟随寻路结果会产生问题。严格的说,Dirichlet domains会产生无效图。
在应用中,节点的放置经常基于障碍的结构。如果障碍不知道它们所属的区域,那么很可能图会变得无效。
为了确保正常执行,可以提供一个备用机制(比如障碍躲避操控行为)来解决这个问题。
实用性
Dirichlet domains用途非常广泛。它很容易编程实现(自动产生连接)并且很容易改变。很容易快速的改变关卡编辑程序的寻路图结构而同时不需要调整改变关卡内容。
4.4.3 可视点法(Points of visibility)
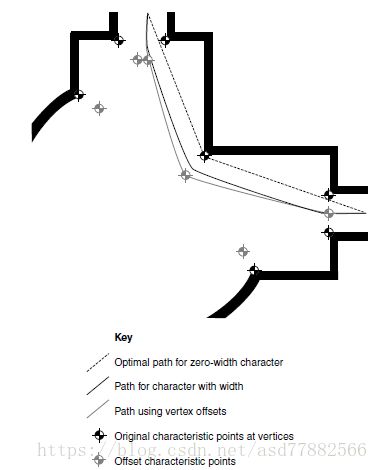
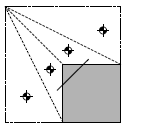
可以看到在2d环境中获得的最优路径在凸顶点处总会有拐点(在路径中刚想改变的点)。如果移动的角色有一个半径,这些拐点需要被替换成一个原理凸点的弧线,如下图示:
在这种情况下,我们可以通过在顶点处外移一点距离选择一个特征点近似的作为拐点。这将不会产生弧线,而产生一个可信的路径。这些新的特征点通过扩充几何一些距离来产生新几何的边。
划分方案
因为拐点自然地出现在最短路径上,我们可以使用它们作为寻路图的节点。
在真实的关卡几何体中会产生太多的拐点。所以需要一个简化的版本,这样我们就可以找到大规模几何变化的拐点。也可以从碰撞几何体中获得这些点,或者通过特殊方式生成。
这些拐点可以作为建造图的节点位置。
为了找出哪些节点相连,可以在它们之间发射射线,如果没有和任意一个几何体发生碰撞就说明有连接。这几乎等于说一个点能够被另一个看到。基于这个原因被称为“可视点”方法。在很多情况下图会很大。一个复杂的凹边形中,会有上百个拐点,他们大多数都能看到对方,如下图示:
量化,本地化,有效性
可视点法经常用来做Dirichlet域中心部分的量化。
此外,如果Dirichlet域被用来量化,被量化成两个连接的节点的点可能并不能到达对方处。正如我们上边提到的,这意味着这个图严格来说无效。
实用性
尽管它严重的缺点,一个可视点方法仍是一个相当流行的图自动生成方法。
然而考虑到这个结果并不值得这个效果,在我们经验中需要很多手动的处理,可能挫败整个项目。建议使用寻路网格替代。
4.4.4 寻路网格
现代的游戏主要使用寻路网格(通常缩写为navmesh)来寻路。寻路中的寻路网格利用关卡设计者已经指定的关卡区域连接,无论游戏中是否有AI。关卡自己是有相连的多边形组成。我们可以使用这个图形结构作为寻路产生的基础。
划分方案
很多游戏使用设计者定义的地板多边形作为网格多边形。每一个多边形作为树中的一个节点,如下图示:
这个树基于关卡的网格几何体因此通常被称作导航网格,或者”navmesh”。如果相应的多边形共用同一条边,那么对应的节点相连。地板多边形通常是三角形,也有可能是四边形。所以对应的节点有三个或四个连接。
创建一个导航网格通常需要设计者在建模包中制定对应的多边形作为地板。他们也可能用这种方式指定音效或者地形控制特征。导航网格除了瓦片图相对其他方法需要更少的干预。
量化和本地化
一个位置被定位在一个包含它的地板多边形中。我们可以查询大量的多边形来找到它,或者我们可以用一致性假设。
一致性基于如果我们知道角色上一帧的位置在哪个节点,他下一帧很有可能在同一个节点或者相邻节点。我们可以先检查这些节点。这个方法在寻多划分方案中都很有用,在导航地图中更关键。
唯一的问题是当一个角色没有碰触地板时。我们可以简单的找到他下边的第一个多边形来量化。不幸的是,这在他下落或者上跳时会选出一个完全不适当的节点。如下图示,角色被量化为房间的底部,虽然他是在上边的通道上。这可能造成重新计划角色的路径到房间的下边,而不是期望效果。
本地化可以选择多边形中的任意一点,但是通常使用多边形的重心(顶点位置的平均值),这在三角形上工作的很好,对正方形或多边形,需要一个凹边形(?应该是凸边形)才能这样工作。在图形引擎中的几何图元也有这样的要求。所以如果我们使用相同的图元来渲染,会很安全。
有效性
被导航网格生成的区域也有可能会有问题。我们已经假设一个区域的任一点可以直接移动到相邻区域的任一点,但是可能并不是这样情况。如下图所辖可能会产生碰撞。
因为地板多边形有关卡设计者创造,这种情况可以通过慎重设计来减轻。
实用性
使用这种方法需要一个额外的处理来考虑对象的几何体。因为不是地板几何体的所有位置都可以放置角色(可能太靠近墙),这个能会影响到寻路连接的生成,这个问题在凸区域(应该指的是障碍)例如门口更明显。
尽管有这个问题,它仍然是一个非常流行的方法。对于一个偶尔需要它的游戏,这种方式提供了额外的好处,例如生成墙上边的路径,穿过天花板或者其他一个情况。或者如果角色需要贴墙会很有用。而其他方式则很难实现。
边作为节点
地板多边形也可以将多边形的边作为寻路图的点把面向的多边形作为连接,如下图示:
这种方式也常用于基于门户的渲染,节点作为门户,所有可以互相看到的门户相连。门户渲染(Portal rendering)是一个图形技术关卡的几何体被分割成多个块,很容易检测哪一些块需要被画出来,来减少渲染时间。完整的细节本书可以在网上查到。
在导航网格中,地板多边形的任一条边都表现为一个门户作为图节点,我们不需要做视线检测。根据定义,凸地板多边形的每一条边都能看到其他边。
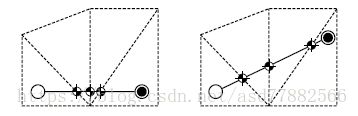
一些文章建议地板多边形边上放置的节点可以动态放置到寻路工作的最好位置,依据当前玩家移动的方向,节点应该对应不同位置,如下图所示:
这是一种连续寻路,章节后边我们会讨论连续寻路算法。在我们看法中,这个方法有些过犹不及,最好使用更快的固定图,如果结果路径看着太曲折,那么路径平滑是一个很好的方法。
多边形作为点或者边作为点的方式都被称作导航网格。所以在讨论时需要清楚讨论的是哪个版本。
4.4.5 非平移问题(Non-Translational Problems)
上边讨论的关于区域和连接只解决的位置的问题。
在一些基于瓦片的游戏中,角色不能够快速转动,所以一个需要转向大角度的角色每一步移动只能轻微转向。
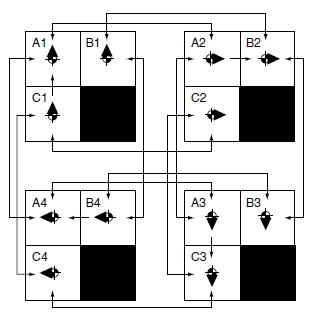
如下图所示,一个角色未移动时不能转向,并且一次只能转90度。节点A1,A2,A3和A4都代表同一位置,但是不同朝向。但是它们拥有不同的连接。角色状态量化到一个图节点需要考虑位置和朝向两种情况。
这样在图中寻路结果将是一系列位移和旋转,上图的寻路计划如下所示:
4.4.6 花费函数(Cost Functions)
在最简单的情况下,在寻路中对最短路径感兴趣。连接的花费代表距离。花费越高,两个节点之间的距离越远。
如果我们想找到最快的路径,那么花费取决于时间。我们可以在一个图中增加各种各样花费的情况。例如在RTS游戏中,暴露在敌人炮火或者更靠近危险地带的连接花费更高。最终路径是最安全的那条。
通常,花费函数是不同情况的混合,对不同的角色会有不同的花费函数。例如一个侦察兵可能对可见度和速度更感兴趣。重炮兵对地形难度更感兴趣。这被称作战术寻路(tactical pathfinding),第六章会讨论。
4.4.7 路径平滑(path smoothing)
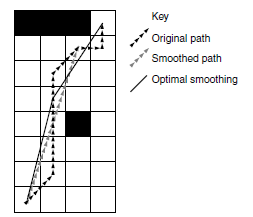
通过图获得到的一个点对点的路径可能看起来很不规则。可视性的节点会更加明显。如下图所示:
一些世界表现相对更加易于平滑路径。门户表现配合可视点连接会获得非常平滑的路径,而基于瓦片的图则很不规则。最终的效果取决于角色跟随路径的表现。如果使用一些路径跟随行为(第三章),那么移动的路径仍然会很平滑。再假设路径需要做平滑处理之前最好先测试一下游戏里的表现。
伪代码
def smoothPath(inputPath):
# 只有两个路径点,是一条直线不需要优化
if len(inputPath) == 2: return inputPath
outputPath - [inputPath[0]]
inputIndex = 2
while inputIndex < len(inputPath) - 1:
if not rayClear(outputPath[len(outputPath) - 1], inputPath[inputIndex]):
outputPath += inputPath[inputIndex - 1]
inputIndex++
# 加入目标点
outputPath += inputPath[len(inputPath) - 1]
return outputPath