TensFlow深度学习(CNN)实现MNIST手写图片识别
一、DNN
上一章博客中讲到用DNN实现MNIST手写图片识别,地址https://blog.csdn.net/lingzw2011/article/details/82225399
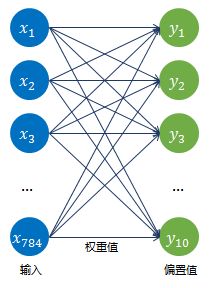
上图是最简单的DNN,所需参数有784 * 10+10=7850个,如果中间加一层隐藏层,如下图:
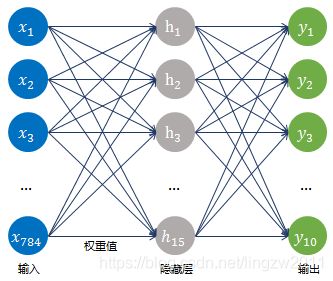
输入和隐藏层的15个神经元连接,就有784 * 15=11760个权重,隐藏层和最后的输出层的10个神经元连接,就有11760 * 10=117600个权重,再加上隐藏层的偏置项15个和输出层的偏置项10个,总共有117625个参数。
DNN存在以下几个问题:
- 参数数量太多
考虑输入一张1000 * 1000像素的图片,输入层有1000 * 1000=100万节点,第一个隐藏层设置有100个节点,仅这一层就有1000 * 1000 * 100=1亿参数。 - 没有利用像素之间的位置信息
图像领域,每个像素和其周围像素紧密相连,和距离远的像素联系就很小。全连接神经网络中,一个神经元和上一层所有神经元相连,相当于把图像所有像素都等同看待。权重学习最终可能会发现,大量的权重值很小,这种权重无关紧要,所以这种学习很低效。 - 网络层数限制
网络层数越多其表达能力越强,但是通过梯度下降方法训练全连接神经网络很困难,因为全连接神经网络的梯度很难传递超过3层。
二、CNN
图像领域,CNN通过尽可能保留重要的参数,去掉大量不重要的参数,来达到更好的学习效果;主要有三个思路:
- 局部连接
每个神经元不再和上一层的所有神经元相连,而只和一小部分神经元相连,这样就减少了很多参数。 - 权值共享
一组连接可以共享同一个权重,而不是每个连接有一个不同的权重,这样又减少了很多参数。 - 下采样
可以使用池化来减少每层的样本数,进一步减少参数数量。
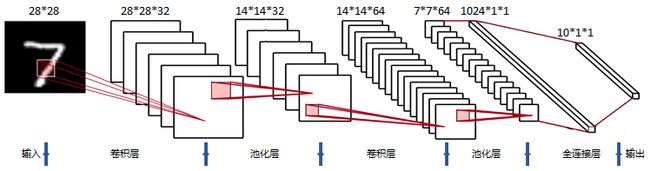
一个卷积神经网络(CNN)由若干个卷积层、池化层、全连接层组成,CNN的经典架构如下图所示:
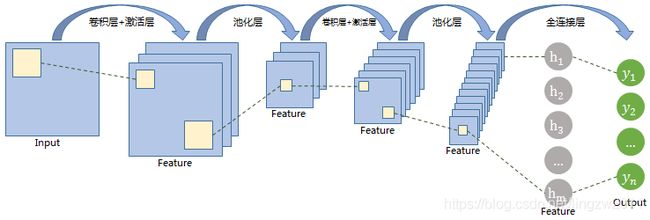
- 输入层:用于数据的输入。
- 卷积层:使用卷积核进行特征提取和特征映射。
- 激活层:由于卷积也是一种线性运算,因此需要增加非线性映射。
- 池化层:进行下采样,对特征图稀疏处理,减少数据运算量。
- 全连接层:通常在CNN的尾部进行重新拟合,减少特征信息的损失。
- 输出层:用于输出结果。
卷积层
假设有一个5 * 5的图像,使用一个3 * 3的filter进行卷积计算,得到一个3 * 3的Feature Map,如下所示:
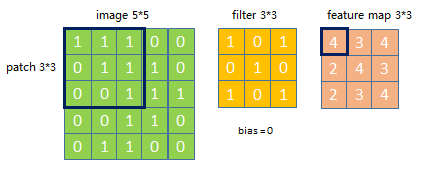
为了清楚的描述卷积计算过程,我们首先对图像的每个像素进行编号,X?,?表示图像的第i行第j列,W?,?表示权重第m行第n列,用b表示偏置项, 卷积计算公式:
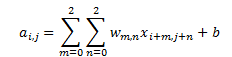
Feature Map的第1行第1列元素的卷积计算方法为:
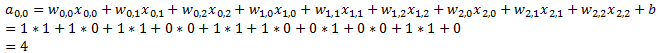
其它的以此类推,逐步滑动,步幅(stride)为1,对整个图像进行卷积计算得到3 * 3的特征图。下面的动画显示了整个Feature Map的计算过程:

激活层
卷积神经网络中,激活函数往往不选择Sigmoid或Tanh函数,而是选择Relu函数。
Relu函数的定义为:f(?)=???(0,?),如下图:

池化层
若得到的 feature map(特征图)依旧比较大,此时可以通过池化层来对每一个 feature map 进行降维操作。一般有两种计算方式:
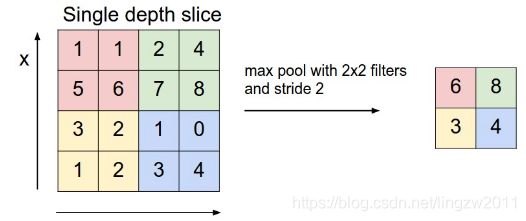
- 最大池化(Max Pooling);提取局部最大值;这是最常用的池化方法。
- 均值池化(Mean Pooling);提取局部均值。
全连接层
全连接层主要对特征进行重新拟合,减少特征信息的丢失。
padding操作
使用CNN对图像进行特征提取,一般会使用TensorFlow中的卷积函数和池化函数来对图像进行卷积和池化操作,而这两种函数中都存在padding操作,是否对输入的图像矩阵边缘补0,'SAME '为补零,'VALID’则不补零。
如下图边缘补零:

下面的动画显示了整个Feature Map的计算过程,白色区域为padding操作:
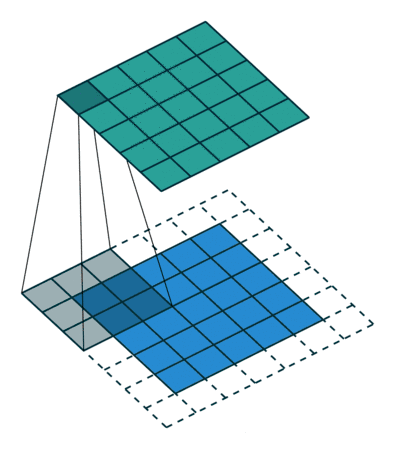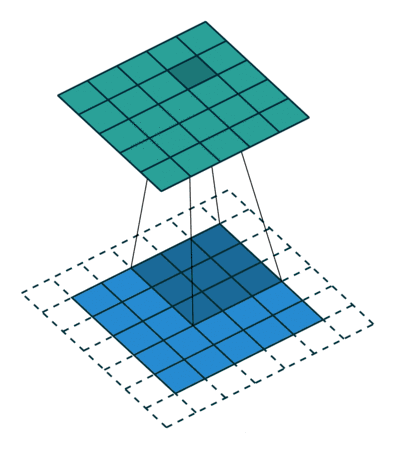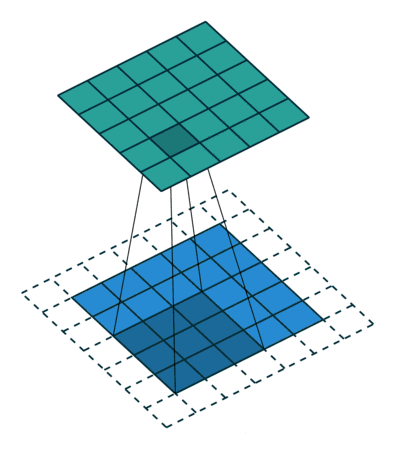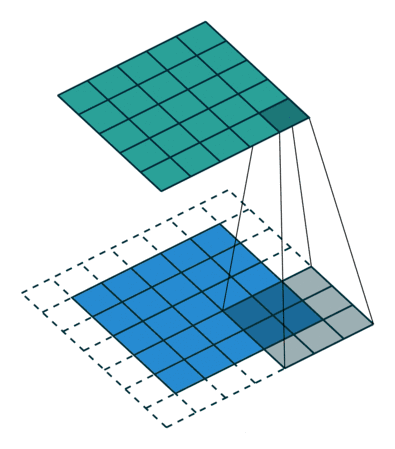
以下是 SAME 模式输出特征图大小和padding大小的计算公式:
输出公式:
- out_height = ceil(in_height / strides)
- out_width = ceil(in_width / strides)
补零公式:
- pad_height = max((out_height - 1) * strides + filter_height - in_height, 0)
- pad_top = floor(pad_height / 2)
- pad_bottom = pad_height - pad_top
- pad_width = max((out_width - 1) * strides + filter_width - in_width, 0)
- pad_left = floor(pad_width / 2)
- pad_right = pad_width - pad_left
三、代码
CNN代码模型结构为:
- 输入层:Mnist数据集(28*28)
- 第一层卷积:感受视野5*5,步长为1,卷积核:设置32个
- 第一层池化:池化视野2*2,步长为2
- 第二层卷积:感受视野5*5,步长为1,卷积核:设置64个
- 第二层池化:池化视野2*2,步长为2
- 全连接层:设置1024个神经元
- 输出层:0~9十个数字类别
# -*- coding: utf-8 -*-
import tensorflow as tf
# 导入input_data用于自动下载和安装MNIST数据集
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 声明一个占位符,None表示输入图片的数量不定,28*28表示图片像素
x = tf.placeholder(tf.float32, [None, 28*28])
# 类别是0-9总共10个类别,对应输出分类结果
y_ = tf.placeholder(tf.float32, shape=[None, 10])
# 权值W
def weight_variable(shape):
# truncated_normal 随机产生一个形状为shape的正态分布,均值为0,标准差为0.1
return tf.Variable(tf.truncated_normal(shape, stddev=0.1))
# 偏置项b
def bias_variable(shape):
# 生成一个形状为shape的常量,初始值为0.1
return tf.Variable(tf.constant(0.1, shape=shape))
# 卷积计算
def conv2d(x, W):
# [1, 1, 1, 1]表示各方向步数为1,SAME:如果不够,边缘外自动补0
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
# 构建池化层
def max_pool(x):
# 池化视野2*2,步长为2
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
"""第一层卷积"""
# 卷积核尺寸大小5*5,灰色图片通道为1,卷积出32个特征
W_conv1 = weight_variable([5, 5, 1, 32])
# 每一个卷积核都有一个对应的偏置项。
b_conv1 = bias_variable([32])
# 把x reshape成了28*28*1的形状,灰色图片通道为1,-1代表图片数量不定
x_image = tf.reshape(x, [-1, 28, 28, 1])
# 卷积计算,加上偏置量,并使用激活函数,卷积结果28x28x32
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
"""第一层池化"""
# 池化结果14x14x32
h_pool1 = max_pool(h_conv1)
"""第二层卷积"""
# 32通道卷积,卷积出64个特征
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
# 卷积结果14x14x64
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
"""第二层池化"""
# 池化结果7x7x64
h_pool2 = max_pool(h_conv2)
"""全连接层"""
# 加入一个有1024个神经元的全连接层
W_fc1 = weight_variable([7*7*64, 1024])
b_fc1 = bias_variable([1024])
# 最后的池化层输出,reshape成一维向量
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
# 矩阵相乘,全连接输出
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# 占位符
keep_prob = tf.placeholder(tf.float32)
# 执行dropout操作,减少过拟合,训练中启用,测试中关闭
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
"""输出层"""
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
# 模型预测输出,矩阵相乘,softmax函数输出
prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
"""模型训练"""
# loss 交叉熵
cross_entropy = -tf.reduce_sum(y_ * tf.log(prediction))
# 模型训练,梯度下降
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 正确预测,得到True或False的List
correct_prediction = tf.equal(tf.argmax(y_, 1), tf.argmax(prediction, 1))
# 将布尔值转化成浮点数,取平均值作为精确度
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# session初始化并调用
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
# 迭代优化模型 迭代20000次
for i in range(20000):
# 每次迭代送入100个样本进行训练
batch_xs, batch_ys = mnist.train.next_batch(100)
# dropout值定义为0.5,关闭50%的神经元
train_step.run(feed_dict={x: batch_xs, y_: batch_ys, keep_prob: 0.5})
# 每迭代100次,做个训练精度统计
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={x: mnist.test.images, y_:mnist.test.labels, keep_prob:1.0})
print("第{0}次训练,准确率:{1}".format(i+100, train_accuracy))
训练的准确率可以达到99%以上,比DNN的准确率高出太多!
菜鸟一枚,发表博客的主要目的是为了记录tensorflow机器学习中的点滴,方便自己以后查阅,如果有错误的地方,还请大家多提宝贵意见。