C语言数据结构之稀疏矩阵（一）

最近开始学习C语言的稀疏矩阵的一些知识，现在简单的整理梳理一下知识脉络，仅供自己总结学习，欢迎技术指正，拒绝盲喷。

1.首先先介绍一下关于稀疏矩阵的一些基础知识，关于稀疏矩阵，一直都没有过很清楚详细的定义。简单的说，在M*N的一个矩阵中，假设有t个元素不为0，那么有计算公式：δ=t/(m*n).称δ为该矩阵的稀疏因子，一般认为当δ<0.05(并无具体规定)的时候称该矩阵为稀疏矩阵。

2.一般在操作稀疏矩阵的时候以压缩存储为主，稀疏矩阵判定的主要标准是矩阵中非零(Non-Zero)元所占的比例，所以稀疏矩阵的压缩基本原理也由此而来，一般需要一个三元组(i,j,Data)来存储稀疏矩阵中的非零元(直接忽略零元)，三元组(i,j,Data)包括矩阵元的行列坐标和元的数值，由此，稀疏矩阵可由非零元的三元组(i,j,Data)集合唯一确定。

例：

M = 

    0  8  0  6  0  2  0

    0  0  34 54 0  0  2

    -7 0  0  0  0  0  0

    0  0  0  0  -12 0 0

M矩阵可由

   （0,1,8）,(0,3,6),(0,6,2),(1,2,34),(1,3,54),(1,6,2),(2,0,-7),(3,4,-12)

的集合唯一表示。

3.下面简单介绍一下利用稀疏矩阵的压缩存储方式进行矩阵的常用运算

转置运算,是矩阵运算中最简单的一种，对于一个m*n的矩阵Matrix与它的转置矩阵Matrix'遵守如下规则：

Matrix(i,j)=Matrix'(j,i);(0≤i＜m，0≤j＜n)

所以我们分析对稀疏矩阵三元组做转置操作共需要两个步骤：

    1)将每个三元组中的i和j互换

    2)对三元组重新排序

具体实现代码如下：

#include 
#include 

/**
* @macro definition
*/
#define MAX_NODE_NUM     100
#define MAX_ROW          4
#define MAX_COL          7

/**
* @Global srtuct
*/
typedef struct 
{
    unsigned int ui32Row, ui32Col;
    int si32Data;
}Struct_DataNode;

typedef struct
{
    Struct_DataNode DataNode[MAX_NODE_NUM];
    unsigned int ui32MatrixRow, ui32MatrixCol, ui32DataNodeNum;
}Struct_SparceMatrix;

/**
* @ main function
*/
int main(void)
{
    Struct_SparceMatrix OriginalMatrix, TransMatrix;
    int si32DataNodeNumTemp = 0;

    memset(&OriginalMatrix,0x00,sizeof(OriginalMatrix));
    memset(&TransMatrix, 0x00, sizeof(TransMatrix));

    /**
    * @Original matrix operations
    */
    OriginalMatrix.ui32MatrixRow = MAX_ROW;
    OriginalMatrix.ui32MatrixCol = MAX_COL;

    int si32OriginalMatrixComplete[MAX_ROW][MAX_COL] = 
    {
        {0,8,0,6,0,2,0},
        {0,0,34,54,0,0,2},
        {-7,0,0,0,0,0,0},
        {0,0,0,0,-12,0,0}
    };

    printf("The Original Matrix[%d,%d] is :\n",
        OriginalMatrix.ui32MatrixRow,
        OriginalMatrix.ui32MatrixCol);
    for (unsigned int i = 0; i < OriginalMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < OriginalMatrix.ui32MatrixCol; ++j)
        {
            printf("%3d,", si32OriginalMatrixComplete[i][j]);

            if (si32OriginalMatrixComplete[i][j])
            {
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].ui32Row = i;
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].ui32Col = j;
                OriginalMatrix.DataNode[OriginalMatrix.ui32DataNodeNum].si32Data = si32OriginalMatrixComplete[i][j];
                ++OriginalMatrix.ui32DataNodeNum;
            }
        }
        printf("\n");
    }

    printf("Original sparse matrix:\n");
    for (unsigned int i = 0; i < OriginalMatrix.ui32DataNodeNum; ++i)
    {
        printf("[%d,%d,%d]\n",OriginalMatrix.DataNode[i].ui32Row,
                                OriginalMatrix.DataNode[i].ui32Col,
                                OriginalMatrix.DataNode[i].si32Data);
    }

    /**
    * @Transposition matrix operations
    */
    TransMatrix.ui32DataNodeNum = OriginalMatrix.ui32DataNodeNum;
    TransMatrix.ui32MatrixCol = OriginalMatrix.ui32MatrixRow;
    TransMatrix.ui32MatrixRow = OriginalMatrix.ui32MatrixCol;

    printf("Transposition sparse matrix:\n");
    for (unsigned int i = 0,ui32DataNodeNumTemp = 0; i < TransMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < TransMatrix.ui32DataNodeNum; ++j)
        {
            if (i == OriginalMatrix.DataNode[j].ui32Col)
            {
                TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row = OriginalMatrix.DataNode[j].ui32Col;
                TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col = OriginalMatrix.DataNode[j].ui32Row;
                TransMatrix.DataNode[ui32DataNodeNumTemp].si32Data = OriginalMatrix.DataNode[j].si32Data;
                printf("[%d,%d,%d]\n", TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row,
                                        TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col,
                                        TransMatrix.DataNode[ui32DataNodeNumTemp].si32Data);
                ++ui32DataNodeNumTemp;
            }
        }
    }

    printf("The Transposition Matrix[%d,%d] is :\n",
        TransMatrix.ui32MatrixRow,
        TransMatrix.ui32MatrixCol);
    for (unsigned int i = 0, ui32DataNodeNumTemp = 0; i < TransMatrix.ui32MatrixRow; ++i)
    {
        for (unsigned int j = 0; j < TransMatrix.ui32MatrixCol; ++j)
        {
            if (i == TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Row &&
                j == TransMatrix.DataNode[ui32DataNodeNumTemp].ui32Col)
            {
                printf("%3d,",TransMatrix.DataNode[ui32DataNodeNumTemp++].si32Data);
            }
            else
            {
                printf("%3d,", 0);
            }
        }
        printf("\n");
    }    
    return 0;
}

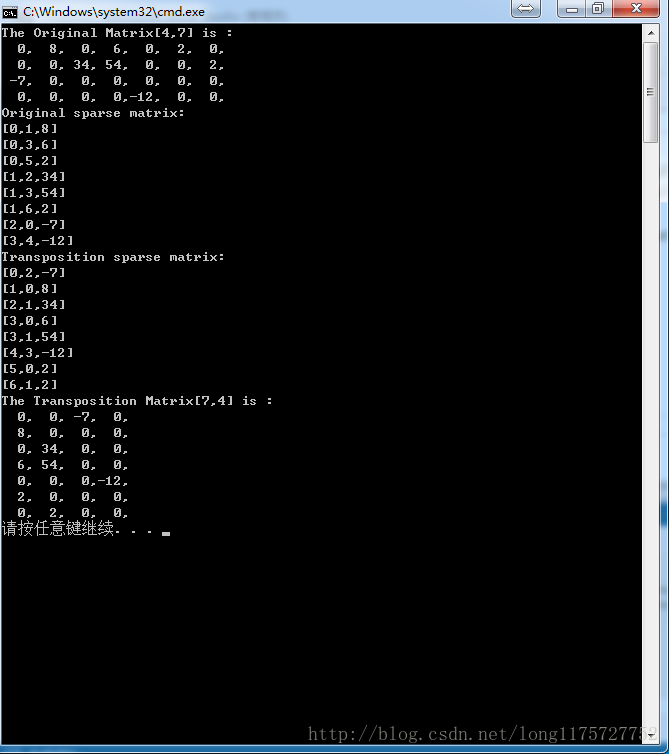
以上代码的控制台输出如下：

由此可看到，通过稀疏矩阵的三元组表示形式计算矩阵的转置结果是正确的。

4.最后注意总结的是，在做以三元组做矩阵转置的时候，代码段的时间复杂度是O(TransMatrix.ui32MatrixRow * TransMatrix.ui32DataNodeNum)，可以看出矩阵的行数以及非零元的个数乘积是成正比的，矩阵转置的经典算法时间复杂度为O(Row * Col)，当ui32DataNodeNum比较大的时候，时间复杂度比较大。

5.另外，做嵌入式C的同学(尤其单片机开发或者IC开发)，对代码的时间开销和空间开销都非常的在意，对于时间开销的优化需要依据不同场合采用不同的算法，对于空间开销，此段代码可以采用动态内存申请(malloc)的方法进行优化。