LeetCode030——与所有单词相关联的字串

我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/substring-with-concatenation-of-all-words/description/

题目描述：

知识点：哈希表、滑动窗口

思路一：用一个哈希表存储words数组中出现的单词及其次数，单指针遍历字符串s中的每一个字符判断其是否是恰好串联words中所有单词的子串的起始位置

如果想到了哈希表的思想，该思路是最自然能想到的一个思路。该思路的步骤如下：

（1）新建一个哈希表hashMap，其键为words数组中出现的单词，其值为该单词在words数组中出现的次数。

（2）对于字符串s中的每一个字符，我们都需要新建一个和hashMap一模一样的哈希表tempMap，该哈希表用以判断该字符是否是恰好串联words中所有单词的子串的起始位置。

（3）如果tempMap中有该单词，那么将该单词在tempMap中对应的次数减1。这也是我们为什么要新建一个和hashMap一模一样的哈希表tempMap的原因，因为我们每次都会改变tempMap的值。而如果我们改变了hashMap的值，那么下一轮字符的参照表就不见了。如果没有该单词，直接判断字符串s中该位置的字符不是我们所要寻找的字符。

几个注意点：

（1）如果words中没有任何元素，我们返回的是一个空集合。

（2）我们不需要遍历字符串s中的每一个字符，我们只需要遍历字符串s中索引在0 ~ s.length() - num * len之间的字符即可，其中num为words数组的元素个数，len为words数组中的单词的长度。因为再往后遍历的话，所得到的字符串的长度都小于num * len了，显然是不满足条件的。

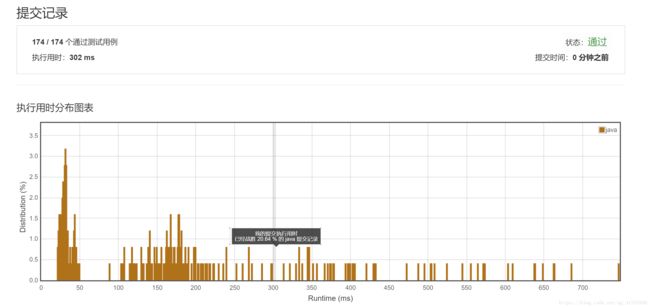
生成哈希表这个过程的时间复杂度是O(num)，而循环遍历字符串s中的字符并判断该字符是否是恰好串联words中所有单词的子串的起始位置的过程的时间复杂度是O(s.length() * num)，因此总的时间复杂度是O(s.length() * num)。而对于空间复杂度，我们使用了一个哈希表，所以是O(diff_num)级别的，其中diff_num为words数组中不重复元素的数目。

JAVA代码：

public class Solution {

	public List findSubstring(String s, String[] words) {
		List result = new ArrayList<>();
		if(words.length == 0) {
			return result;
		}
		//num represents the length of words array
		int num = words.length;
		//len represents the length of words[0]
		int len = words[0].length();
		//Create a hashMap whose key are Strings in words array and values are there appearance times in words array
		HashMap hashMap = new HashMap<>();
		for(int i = 0; i < num; i++) {
			if(hashMap.containsKey(words[i])) {
				hashMap.put(words[i], hashMap.get(words[i]) + 1);
			}else {
				hashMap.put(words[i], 1);
			}
		}
		for(int i = 0; i < s.length() - num * len + 1; i++) {
			HashMap tempMap = new HashMap<>(hashMap);
			int j = 0;
			for(; j < words[0].length() * num; j += words[0].length()) {
				String subString = s.substring(i + j, i + j + len);
				if(!tempMap.containsKey(subString)) {
					break;
				}else {
					tempMap.put(subString, tempMap.get(subString) - 1);
					if(tempMap.get(subString) == 0) {
						tempMap.remove(subString);
					}
				}
			}
			if(j >= len * num) {
				result.add(i);
			}
		}
		return result;
	}
}

LeetCode解题报告：

思路二：用一个哈希表存储words数组中出现的单词及其次数，用滑动窗口法来寻找恰好可以串联words中所有单词的子串的起始位置

这道题的题目中其实传递了一个很重要的信息：一些长度相同的words。长度相同意味着什么呢？

我们可以联系一下LeetCode003——无重复字符的最长子串中的滑动窗口法，惊奇地发现这题完全可以用滑动窗口法来解决！

对于每一个单词，既然它们的长度都相同，我们完全可以把它们看作是一个点来处理。但是我们也要注意不同之处，这里的滑动窗口的左右边界每一次行进的距离都是len，其中len为words数组中的单词的长度。因此我们需要使用len个滑动窗口，它们的起始位置分别是0、1、2、……、len - 1。

在处理每一个滑动窗口的时候我们都需要新建一个空的哈希表window，该哈希表用来记录我们的滑动窗口中包含的单词及其次数。

我们的滑动窗口的left指针指向的是滑动窗口中包含的第一个单词的第一个字符的位置，而right指针指向的是滑动窗口中包含的最后一个单词的最后一个字符的后一个位置，也就是说[left, right - 1]中包含的是我们的滑动窗口中的字符。初始化left和right指针均等于滑动窗口的起始位置i。

我们滑动窗口的滑动过程如下：

（1）判断right指针的右边的即将进入滑动窗口的单词subStringRight是否包含在hashMap中，此处的hashMap即思路一中建立的hashMap。如果subStringRight没有包含在hashMap中，很简单，我们更新right的值为right + len，left的值和right相等，清空哈希表window，并continue跳过本次循环即可。

（2）如果subStringRight包含在hashMap中，将subStringRight加入到window。如果window中包含的subStringRight的数量大于hashMap中包含的subStringRight的数量，我们需要移动我们的left指针直至window中包含的subStringRight的数量小于等于hashMap中包含的subStringRight的数量，每次移动的距离也是len。

（3）如果right - left == num * len，其中num为words数组的元素个数，len为words数组中的单词的长度，说明我们找到了满足条件的一个滑动窗口，其左边界指针left就是恰好可以串联words中所有单词的子串的起始位置。

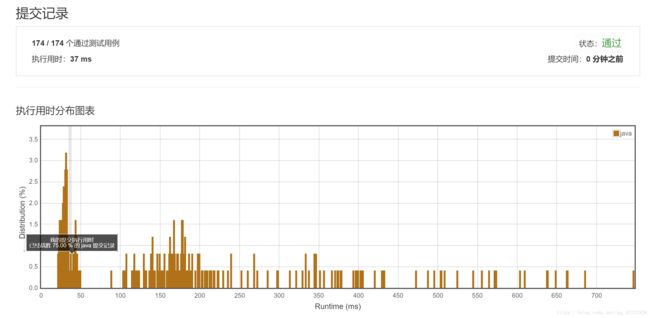
生成哈希表这个过程的时间复杂度是O(num)，而滑动窗口法寻找恰好可以串联words中所有单词的子串的起始位置的过程的时间复杂度是O(s.length())。如果s.length() < num，肯定是不能找到任何值的，因此总的时间复杂度为O(s.length())。而对于空间复杂度，我们使用了一个哈希表，所以是O(diff_num)级别的，其中diff_num为words数组中不重复元素的数目。

JAVA代码：

public class Solution {
	
	public List findSubstring(String s, String[] words) {
		List result = new ArrayList<>();
		if(words.length == 0) {
			return result;
		}
		//num represents the length of words array
		int num = words.length;
		//len represents the length of words[0]
		int len = words[0].length();
		//Create a hashMap whose key are Strings in words array and values are there appearance times in words array
		HashMap hashMap = new HashMap<>();
		for(int i = 0; i < num; i++) {
			if(hashMap.containsKey(words[i])) {
				hashMap.put(words[i], hashMap.get(words[i]) + 1);
			}else {
				hashMap.put(words[i], 1);
			}
		}
		for(int i = 0; i < len; i++) {
			//floating window[left, right - 1]
			HashMap window = new HashMap<>();
			int left = i;
			int right = i;
			while(right < s.length() - len + 1 && left < s.length() - len * num + 1) {
				String subStringRight = s.substring(right, right + len);
				if(!hashMap.containsKey(subStringRight)) {
					right += len;
					left = right;
					window.clear();
					continue;
				}
				if(!window.containsKey(subStringRight)) {
					window.put(subStringRight, 1);	
				}else {
					window.put(subStringRight, window.get(subStringRight) + 1);					
				}
				right += len;	
				while(window.get(subStringRight) > hashMap.get(subStringRight)) {
					String subStringLeft = s.substring(left, left + len);
					window.put(subStringLeft, window.get(subStringLeft) - 1);
					if(window.get(subStringLeft) == 0){
						window.remove(subStringLeft);
					}
					left += len;
				}
				if(right - left == num * len) {
					result.add(left);
				}
			}
		}
		return result;
	}
}

LeetCode解题报告：