蓝桥杯2014年第五届决赛C_C++程序设计本科B组

1.年龄巧合

小明和他的表弟一起去看电影，有人问他们的年龄。小明说：今年是我们的幸运年啊。我出生年份的四位数字加起来刚好是我的年龄。表弟的也是如此。已知今年是2014年，并且，小明说的年龄指的是周岁。
请推断并填写出小明的出生年份。

---

2. 出栈次序

X星球特别讲究秩序，所有道路都是单行线。一个甲壳虫车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。
路边有个死胡同，只能容一辆车通过，是临时的检查站，如图【p1.png】所示。

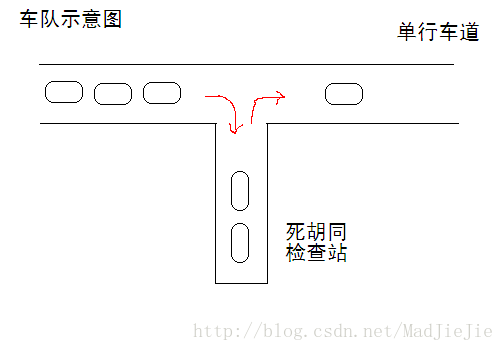
X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。
如果车辆进入检查站和离开的次序可以任意交错。那么，该车队再次上路后，可能的次序有多少种？ 为了方便起见，假设检查站可容纳任意数量的汽车。
显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。 现在足足有16辆车啊，亲！需要你计算出可能次序的数目。

---

递推公式：cur=pre*(4n-2)/(n+1);

#include   

int main()
{  
    long long pre=1;  
    long long cur=1;  

    for(int i=1;i<=16;i++)
    {  
        cur=pre*(4*i-2)/(i+1);  
        pre=cur;  
    }  

    printf("%lld\n",cur);  

    return 0;  
}  

---

3. 信号匹配

从X星球接收了一个数字信号序列。 现有一个已知的样板序列。需要在信号序列中查找它首次出现的位置。这类似于串的匹配操作。
如果信号序列较长，样板序列中重复数字较多，就应当注意比较的策略了。可以仿照串的KMP算法，进行无回溯的匹配。这种匹配方法的关键是构造next数组。
next[i]表示第i项比较失配时，样板序列向右滑动，需要重新比较的项的序号。如果为-1，表示母序列可以进入失配位置的下一个位置进行新的比较。
下面的代码实现了这个功能，请仔细阅读源码，推断划线位置缺失的代码。

// 生成next数组 
int* make_next(int pa[], int pn)
{
    int* next = (int*)malloc(sizeof(int)*pn);
    next[0] = -1;
    int j = 0;
    int k = -1;
    while(j < pn-1){
        if(k==-1 || pa[j]==pa[k]){
            j++;
            k++;
            next[j] = k;
        }
        else
            k = next[k];
    }

    return next;
}

// da中搜索pa， da的长度为an, pa的长度为pn 
int find(int da[], int an, int pa[], int pn)
{
    int rst = -1;
    int* next = make_next(pa, pn);
    int i=0;  // da中的指针 
    int j=0;  // pa中的指针
    int n = 0;
    while(iif(da[i]==pa[j] || j==-1){
            i++;
            j++;
        }
        else
            __________________________;  //填空位置

        if(j==pn) {
            rst = i-pn;
            break;
        }
    }

    free(next);

    return rst;
}

int main()
{
    int da[] = {1,2,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,1,2,1,2,3};
    int pa[] = {1,2,1,1,2,1,1,1,2};

    int n = find(da, sizeof(da)/sizeof(int), pa, sizeof(pa)/sizeof(int));
    printf("%d\n", n);

    return 0;
}

answer: j=next[j]

---

4. 生物芯片

X博士正在研究一种生物芯片，其逻辑密集度、容量都远远高于普通的半导体芯片。 博士在芯片中设计了 n个微型光源，每个光源操作一次就会改变其状态，即：点亮转为关闭，或关闭转为点亮。 这些光源的编号从 1 到 n，开始的时候所有光源都是关闭的。博士计划在芯片上执行如下动作： 所有编号为2的倍数的光源操作一次，也就是把 2 4 6 8 … 等序号光源打开
所有编号为3的倍数的光源操作一次, 也就是对 3 6 9 … 等序号光源操作，注意此时6号光源又关闭了。
所有编号为4的倍数的光源操作一次。 ….. 直到编号为 n 的倍数的光源操作一次。
X博士想知道：经过这些操作后，某个区间中的哪些光源是点亮的。
【输入格式】 3个用空格分开的整数：N L R (L < R < N < 10^15) N表示光源数，L表示区间的左边界，R表示区间的右边界。
【输出格式】 输出1个整数，表示经过所有操作后，[L,R]区间中有多少个光源是点亮的。
例如：
输入：
5 2 3
程序应该输出：
2
再例如：
输入：
10 3 6
程序应该输出：
3

---

也就是从2开始，是因子就操作一次，因子数为奇数就能保证开灯了。

所以只要求得范围内完全平方数的个数即可

int main(void)
{

    long L,R,N;  
    scanf("%ld%ld%ld",&N,&L,&R);  
    long l=(long)sqrt(L-1);  
    long r=(long)sqrt(R);  

    printf("%ld\n",R-L+1-(r-l));      

    return 0;  
}

---

5. Log大侠

atm参加了速算训练班，经过刻苦修炼，对以2为底的对数算得飞快，人称Log大侠。 一天，Log大侠的好友 drd有一些整数序列需要变换，Log大侠正好施展法力… 变换的规则是： 对其某个子序列的每个整数变为: [log_2 (x) + 1] 其中[] 表示向下取整，就是对每个数字求以2为底的对数，然后取下整。 例如对序列 3 4 2 操作一次后，这个序列会变成 2 3 2。drd需要知道，每次这样操作后，序列的和是多少。

【输入格式】 第一行两个正整数 n m 。 第二行 n 个数，表示整数序列，都是正数。 接下来 m 行，每行两个数 L R 表示 atm这次操作的是区间 [L, R]，数列序号从1开始。
【输出格式】 输出 m 行，依次表示 atm 每做完一个操作后，整个序列的和。
例如，
输入：
3 3
5 6 4
1 2
2 3
1 3
程序应该输出：
10
8
6

【数据范围】

对于 30% 的数据， n, m <= 10^3
对于 100% 的数据， n, m <= 10^5
资源约定： 峰值内存消耗 < 256M
CPU消耗 < 1000ms 请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。 注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++
标准，不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include ，
不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

#include   
using namespace std;  
int a[100005];  

int log(int n)  
{  
    int sum=1,ans=0;  
    while(sumsum*=2;  
        ans++;  
    }  
    if(sum==n)  
        return ans+1;  
    return ans;  

}  

int main()  
{  
    int n,m,l,r,sum=0;  
    cin>>n>>m;  
    for(int i=1; i<=n; i++)  
    {  
        cin>>a[i];  
        sum+=a[i];  
    }  
    for(int i=1; i<=m; i++)  
    {  
        cin>>l>>r;  
        for(int j=l; j<=r; j++)  
        {  
            sum-=a[j];  
            a[j]=log(a[j]);  
            sum+=a[j];  
        }  
        cout<<sum<return 0;  
}  

---

6. 殖民地

带着殖民扩张的野心，Pear和他的星际舰队登上X星球的某平原。为了评估这块土地的潜在价值，Pear把它划分成了M*N格，每个格子上用一个整数（可正可负）表示它的价值。
Pear要做的事很简单——选择一些格子，占领这些土地，通过建立围栏把它们和其它土地隔开。对于M*N的格子，一共有(M+1)N+M(N+1)条围栏，即每个格子都有上下左右四个围栏；不在边界上的围栏被相邻的两个格子公用。大概如下图【p1.png】所示。
图中，蓝色的一段是围栏，属于格子1和2；红色的一段是围栏，属于格子3和4。
每个格子有一个可正可负的收益，而建围栏的代价则一定是正的。
你需要选择一些格子，然后选择一些围栏把它们围起来，使得所有选择的格子和所有没被选的格子严格的被隔开。选择的格子可以不连通，也可以有“洞”，即一个连通块中间有一些格子没选。注意，若中间有“洞”，那么根据定义，“洞”和连通块也必须被隔开。
Pear的目标很明确，花最小的代价，获得最大的收益。 【输入数据】 输入第一行两个正整数M N，表示行数和列数。 接下来M行，每行N个整数，构成矩阵A，A[i,j]表示第i行第j列格子的价值。
接下来M+1行，每行N个整数，构成矩阵B，B[i,j]表示第i行第j列上方的围栏建立代价。
特别的，B[M+1,j]表示第M行第j列下方的围栏建立代价。
接下来M行，每行N+1个整数，构成矩阵C，C[i,j]表示第i行第j列左方的围栏建立代价。
特别的，C[i,N+1]表示第i行第N列右方的围栏建立代价。

【输出数据】 一行。只有一个正整数，表示最大收益。

【输入样例1】 3 3 65 -6 -11 15 65 32
-8 5 66 4 1 6 7 3 11 23 21 22 5 25 22 26 1 1 13 16 3 3 4 6 3 1 2

程序应当输出： 123

【输入样例2】 6 6 72 2 -7 1 43 -12 74 74 -14 35 5 3 31 71 -12 70 38 66 40 -6
8 52 3 78 50 11 62 20 -6 61 76 55 67 28 -19 68 25 4 5 8 30 5 9 20 29
20 6 18 3 19 20 11 5 15 10 3 19 23 6 24 27 8 16 10 5 22 28 14 1 5 1 24
2 13 15 17 23 28 24 11 27 16 12 13 27 19 15 21 6 21 11 5 2 3 1 11 10
20 9 8 28 1 21 9 5 7 16 20 26 2 22 5 12 30 27 16 26 9 6 23

程序应当输出 870

【数据范围】 对于20%的数据，M,N<=4 对于50%的数据，M,N<=15 对于100%的数据，M,N<=200
A、B、C数组（所有的涉及到的格子、围栏输入数据）绝对值均不超过1000。根据题意，A数组可正可负，B、C数组均为正整数。

资源约定： 峰值内存消耗 < 256M CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。 注意:
所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

---