2021秋招-算法-位操作
LeetCode–位操作
基础知识点整理
与、或、非、亦或
1. 与(&)运算: 0&0=0,0&1=0,1&0=0,1&1=1
1.1 常用作二进制进位符号计算; 1&1–> 1 此时需要进位;
2. 非(~)运算: ~0=1, ~1 = 0
3. 或(|)运算: 0|0=0, 0|1=1, 1|0=1, 1|1=1
4. 异或(^)运算: 同为假,异为真 : 0^ 0=0, 0^ 1=1, 1^ 0=1, 1^1=0
4.1 常用作 二进制 不进位加法:
0 + 0 -> 0;
1 + 1 -> 0;
1 + 0 -> 1;
0 + 1 -> 1:
num&&0XFFFFFFFF --> num 本身取值操作
nums ^ 0XFFFFFFFF --> 按位取反操作
problem1: 剑指offer-- 二进制加法 (2020-06-19)
注意: 后面 负数 补码转换成 10进制负数过程
# -*- coding:utf-8 -*-
class Solution:
def Add(self, num1, num2):
# write code here
# python中数字是变长,所以 限制位数
xorNum = num1 ^ num2
andNum = (num1 & num2) << 1
while andNum != 0:
tmp1 = xorNum ^ andNum
tmp2 = (xorNum & andNum) << 1
tmp1 = tmp1 & 0xFFFFFFFF
xorNum = tmp1
andNum = tmp2
# xorNum : 负数的补码
return xorNum if xorNum <= 0x7FFFFFFF else ~(xorNum^0xFFFFFFFF)
# 知识点: (负数)原码 + 补码 = 模
正数、负数 原码-反码-补码
-
原码:
1.1 正数: 其二进制值 5:0000 0101
1.2 负数: 最高位为1, 其余绝对值二进制: -5: 1000 0101 -
反码
2.1 正数: =原码
2.2 负数: 原码最高位不变,其余位取反, -5 : 1111 1010 -
补码
3.1 正数: =原码
3.2 负数:反码最后一位 +1, -5:1111 1010 + 1 = 1111 1011 -
负数:
4.1 原码 --> 补码 :
1)最高符号位不变
2)其余位取反
3)最后一位 + 1
4.2 补码 -> 原码
A1)补码最高位不变
A2)-1
A3)其余位取反
B1) 补码最高位不变
B2) 其余位取反
B3) +1
problem2: 剑指offer– 数字二进制表示中1的个数
- 数组逆序遍历: nums = [1, 2, 3, 4]
for i in range(10): #
正序遍历:
range(10):默认step=1,start=0,生成可迭代对象,包含[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
range(1,10):指定start=1,end=10,默认step=1,生成可迭代对象,包含[1, 2, 3, 4, 5, 6, 7, 8, 9]
range(1,10,2):指定start=1,end=10,step=2,生成可迭代对象,包含[1, 3, 5, 7, 9]
逆序遍历:
range(9,-1,-1):step=-1,start=9,生成可迭代对象,包含[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
leetcode-67. 二进制求和-简单(2020-06-23每日一题)
67. 二进制求和-整体难度小于之前返回整数(负数补码到原码的转换)
给你两个二进制字符串,返回它们的和(用二进制表示)。
输入为 非空 字符串且只包含数字 1 和 0。
示例 1:
输入: a = "11", b = "1"
输出: "100"
示例 2:
输入: a = "1010", b = "1011"
输出: "10101"
class Solution:
def addBinary(self, a: str, b: str) -> str:
# 二进制求和
xorNum = int(a, 2) ^ int(b, 2)
addNum = (int(a, 2) & int(b, 2)) << 1
print(xorNum, addNum)
while addNum != 0:
tmp1 = xorNum ^ addNum
tmp2 = (xorNum & addNum) << 1
xorNum = tmp1
addNum = tmp2
return bin(xorNum)[2:]
leetcode: 137.(剑指offer) 只出现一次的数字 II-中等-未作
137. 只出现一次的数字 II
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,3,2]
输出: 3
示例 2:
输入: [0,1,0,1,0,1,99]
输出: 99
# python
leetcode-136.(AC)只出现一次的数字-简单
136. 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# 位操作: 亦或操作, 然后最终结果就是答案
res = nums[0]
for i in range(1, len(nums)):
res = res ^ nums[i]
return res
leetcode:260.(剑指offer)只出现一次的数字 III-中等
# 同: 剑指 Offer 56 - I.(同LC-260) 数组中数字出现的次数-中等
剑指 Offer 56 - I.(同LC-260) 数组中数字出现的次数-中等
剑指 Offer 56 - I. 数组中数字出现的次数
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
示例 1:
输入:nums = [4,1,4,6]
输出:[1,6] 或 [6,1]
示例 2:
输入:nums = [1,2,10,4,1,4,3,3]
输出:[2,10] 或 [10,2]
官方解读: 方法一:分组异或
思路
让我们先来考虑一个比较简单的问题:
如果除了一个数字以外,其他数字都出现了两次,那么如何找到出现一次的数字?
答案很简单:全员进行异或操作即可。考虑异或操作的性质:对于两个操作数的每一位,相同结果为 00,不同结果为 11。那么在计算过程中,成对出现的数字的所有位会两两抵消为 00,最终得到的结果就是那个出现了一次的数字。
那么这一方法如何扩展到找出两个出现一次的数字呢?
如果我们可以把所有数字分成两组,使得:
- 两个只出现一次的数字在不同的组中;
- 相同的数字会被分到相同的组中。
那么对两个组分别进行异或操作,即可得到答案的两个数字。这是解决这个问题的关键。
class Solution:
def singleNumbers(self, nums: List[int]) -> List[int]:
# 异或结果
ret = reduce(lambda x, y: x^y, nums)
# 找到分组元素: 异或结果为1,代表两个数当前位置不同,然后使用1做与运算,切分开两个数;
div = 1
while div & ret == 0:
div <<= 1
# 0 ^ x 同样 = x
a, b = 0, 0
for num in nums:
# 位操作转为bool判断: 如果结果不为0,则代表 True; 如果结果为0, 则代表 False;
if num & div:
a = a ^ num
else:
b = b ^ num
return [a, b]
思考&总结
1. 异或操作(^):可用作二进制加法(无进位), 同样如果 两数相等,异或结果为0;
2. 本体巧妙之处在于分组操作的选择, 在 异或结果中选取 1 的位置,利用这个数,将数组分为两组,分别异或;
3. 与操作的 False/True判断: 如果结果不为0,则代表True; 如果结果为0, 则代表False
剑指 Offer 56 - II. (同leetcode137)数组中数字出现的次数 II-中等-不会
剑指 Offer 56 - II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
示例 1:
输入:nums = [3,4,3,3]
输出:4
示例 2:
输入:nums = [9,1,7,9,7,9,7]
输出:1
朴素做法: 按二进制位 统计, 每一位的 1的个数;
解题思路:如果数组中的数字除一个只出现一次之外,其他数字都出现了两次。
我们可以如Solution56_1一样用异或位运算(^)解决这个问题。
上述思路不能解决这里的问题,因为三个相同的数字的异或结果还是该数字。尽管我们这里不能应用异或运算,
我们还是可以沿用位运算的思路。
如果一个数字出现三次,那么它的二进制表示的每一位(0或者1)也出现三次。
如果把所有出现三次的数字的二进制表示的每一位都分别加起来,那么每一位的和都能被3整除。
如果某一位的和能被3整除,那么那个只出现一次的数字二进制表示中对应的那一位是0;否则就是1;
上述思路同样适用于数组中一个数字出现一次,其他数字出现奇数次问题(如果是偶数次,直接用异或就可)。
这种解法的时间效率是O(n)。我们需要一个长度为32的辅助数组存储二进制表示的每一位的和。由于数组的长度是固定的,因此空间效率是O(1)。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
# 按照32位进行遍历
for i in range(32):
cnt = 0 # 记录当前 bit 有多少个 1
bit = 1 << i # 记录当前要操作的 bit 1 10 100 1000
# 进行按位与
for num in nums:
if num & bit :
cnt += 1 # 当前数字 当前bit 为1
# 不等于0说明唯一出现的数字在这个 bit 上是1
# 或操作相当于 res按照 位 进行了整理: 100 | 1001 = 1001, 也就是将某一个位置变为1. 其他不变。
if cnt % 3 != 0: # 当前位 出现一次数字 bit 为1
res = res | bit # 0 | (11 11 11 100) 0 | 100 --》 100
# 说明: 负数原因: 32位, 最高位是符号位: 1111 1111 1111 1111 1111 1111
# 2**31代表整数最大范围; 大于 2**31 则符号位为1, 变为负数, 补码+源码= 模; res为补码, res - 2**32即可;
# return res if res <= 2**31 else res - 2**32
return res if res <= 0x7FFFFFFF else ~(res^0xFFFFFFFFF)
大佬自动机做法-不会
参考代码:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ones, twos = 0, 0
for num in nums:
ones = ones ^ num & ~twos
twos = twos ^ num & ~ones
return ones
leetcode-421. 数组中两个数的最大异或值-中等-未AC
421. 数组中两个数的最大异或值
给定一个非空数组,数组中元素为 a0, a1, a2, … , an-1,其中 0 ≤ ai < 231 。
找到 ai 和aj 最大的异或 (XOR) 运算结果,其中0 ≤ i, j < n 。
你能在O(n)的时间解决这个问题吗?
示例:
输入: [3, 10, 5, 25, 2, 8]
输出: 28
解释: 最大的结果是 5 ^ 25 = 28.
# 自己思路
1. 异或性质: 同为0, 异为1, 结果最大, 贪心思路, 最大的数和保证最后结果大的另一个数字;
25 | 1 1 0 0 1
10 | 1 0 1 0
8 | 1 0 0 0
5| 0 1 0 1
3| 0 0 1 1
2| 0 0 1 0
异或结果大: 贪心: 从高位到最低位尽量保证 异或结果为1;
但是具体怎么保证最后结果最好想不明白。。。
官方题解-数组中两个数的最大异或值
方法一:利用哈希集合存储按位前缀
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
# length of max number in a binary representation
L = len(bin(max(nums))) - 2
max_xor = 0
for i in range(L)[::-1]:
# go to the next bit by the left shift
max_xor <<= 1
# set 1 in the smallest bit
curr_xor = max_xor | 1
# compute all existing prefixes
# of length (L - i) in binary representation
prefixes = {num >> i for num in nums}
# Update max_xor, if two of these prefixes could result in curr_xor.
# Check if p1^p2 == curr_xor, i.e. p1 == curr_xor^p2
max_xor |= any(curr_xor^p in prefixes for p in prefixes)
return max_xor
powcai大佬实现-看了很多他的题解
# python --- 未理解
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
res = 0
mask = 0
for i in range(31, -1, -1):
mask = mask | (1 << i)
# 记录前缀
s = set()
for num in nums:
s.add(num & mask)
# 假设最大值
tmp = res | (1 << i)
for t in s:
if tmp ^ t in s:
res = tmp
break
return res
自己重新实现;
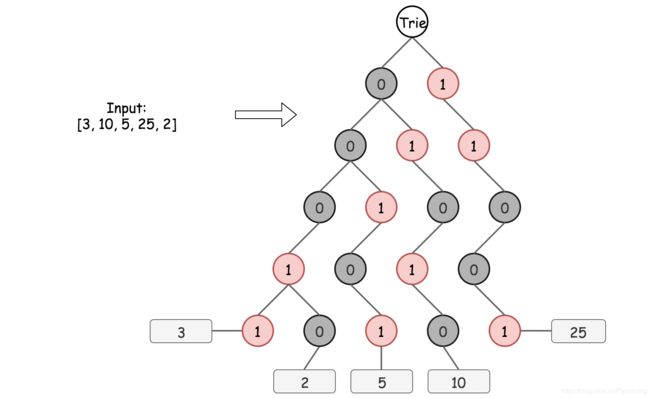
方法2: 逐位字典树
# powcai大佬
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
if not nums: return 0
# 创建前缀树
root = {}
for num in nums:
cur = root
for i in range(31, -1, -1):
cur_bit = (num >> i) & 1
cur.setdefault(cur_bit, {})
cur = cur[cur_bit]
res = float("-inf")
# 按位找最大值
for num in nums:
cur = root
cur_max = 0
for i in range(31, -1, -1):
cur_bit = (num >> i) & 1
if cur_bit ^ 1 in cur:
cur_max += (1 << i)
cur = cur[cur_bit ^ 1]
else:
cur = cur[cur_bit]
res = max(res, cur_max)
return res
为了最大化异或值,需要在每一步找到当前比特值的互补比特值。下图展示了 25 在每一步要怎么走才能得到最大异或值:
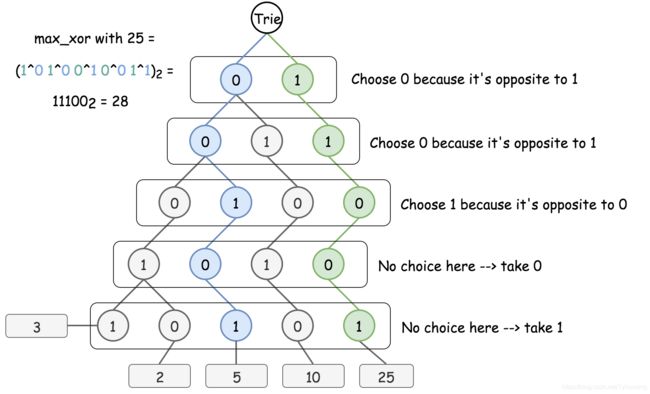
实现方式也很简单:
-
如果当前比特值存在互补比特值,访问具有互补比特值的孩子节点,并在异或值最右侧附加一个 1。
-
如果不存在,直接访问具有当前比特值的孩子节点,并在异或值最右侧附加一个 0。
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
# Compute length L of max number in a binary representation
L = len(bin(max(nums))) - 2
# zero left-padding to ensure L bits for each number
nums = [[(x >> i) & 1 for i in range(L)][::-1] for x in nums]
max_xor = 0
trie = {}
for num in nums:
node = trie
xor_node = trie
curr_xor = 0
for bit in num:
# insert new number in trie
if not bit in node:
node[bit] = {}
node = node[bit]
# to compute max xor of that new number
# with all previously inserted
toggled_bit = 1 - bit
if toggled_bit in xor_node:
curr_xor = (curr_xor << 1) | 1
xor_node = xor_node[toggled_bit]
else:
curr_xor = curr_xor << 1
xor_node = xor_node[bit]
max_xor = max(max_xor, curr_xor)
return max_xor