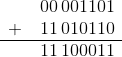浮点数的加法运算
浮点数的加法运算分以下五个步骤：
1、对阶：
这一点和十进制中计算指数一样，首先应该使指数化为相同的指数幂，例如：
x=3*10^4,y=4*10^3,则，x+y=3*10^4+0.4*10^4=(3+0.4)*10^4二进制中也是如此：
x=.1010*2^10,y=.1100*2^01,则,x+y=.1010*2^10+.0110*2^10=(.1010+.0110)*2^102、尾数求和
即：(.1010+.0110)
3、规格化
（负数的补码在左侧补1值不变，正数的补码在左侧补0值bubi不变）
规格化分为左规和右规，左规：如果符号位与位数最高位相同则需要左规，不同则右规，
4、舍入
考虑尾数右移时丢失的数值位。舍入的方式有三种：1、舍0去1，有舍有入比较精确，实现时比较麻烦。2、截去法，直接截去丢失的数值。3、恒1法，直接在尾数最低位置1，有放大也有缩小，还算精确（0.0右移并用恒1法则变为1.对尾数进行了放大，1.1右移的话则变为1.尾数比原来变小）
5、检测溢出
例：
解：阶码取3位，尾数取6位（均不包括符号位），机器表示的形式分别为
![[x]_{CC}=0010\0110100 \par[y]_{CC}=0100\1010110](http://img.e-com-net.com/image/info8/ebd0b6a498eb46f18936fe00657005bf.gif){kind=small}
（CC表示补码）
(1)、对阶：求阶差（两阶码的补码相减）
在机器运算中，符号位在表示时取1位，但是在运算的过程中则是取2位作为符号位
减00100就是加-00100的补码，即11100
其真值是-2，即x的阶码比y的阶码小2，故将x的阶码增大为0100，尾数右移两位变为0100 0001101
(2)、尾数向加
x,y相加的结果为：0100 1 100011
(3)、规格化
符号位与尾数最高位相同，即11.1或00.0，需要左规（符号位与尾数一同左移1位，阶码减1），所以结果应为：
如果符号位出现01.x或10.x则需要右规（符号位与尾数一同右移，阶码加1）
[x+y]补 = 0011 1 000110
x+y = (-0.111010)*2^(+011)(4)、舍入
在对阶和右规的过程中，可能会将尾数的低位丢失，引起误差，影响精度，为此可用舍入法来提高尾数的精度。
例二：
浮点数x=0.1101*x^(+10), y=0.1011*2^(+01),求 x+y, 用0舍1入法。
解：
阶码取2位，尾数取4位（均不包含符号位），机器的表示形式是：
[x]补 = 010 0 1101
[y]补 = 001 0 1011
(1)、对阶
00 10
+ 11 11
----------
00 01
故x的阶码比y的阶码大1，所以，y的阶码加1，尾数右移1位变为01011，用0舍1入法，
知，此时有[y]补 = 010 0 0110
(2)、尾数向加
00 1101
+ 00 0110
------------
01 0011
(3)、规格化
尾数符号位为01，所以需要右规（尾数右移1位，阶码加1）
[x+y]补 = 011 0 10011
0舍1入后得到，[x+y]补 = 011 0 1010
故：x+y = 01010*2^(+11)