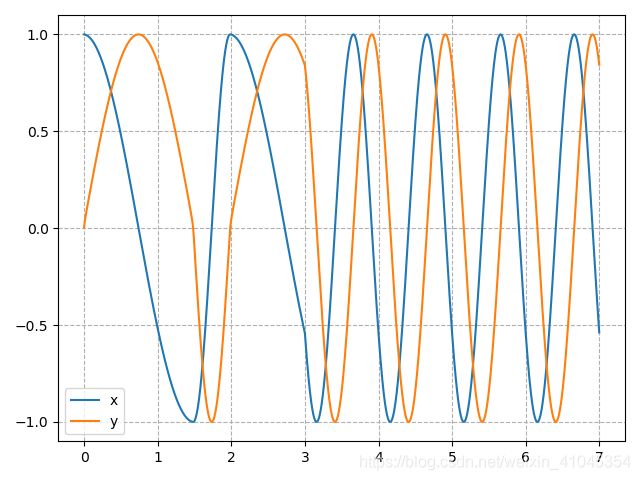
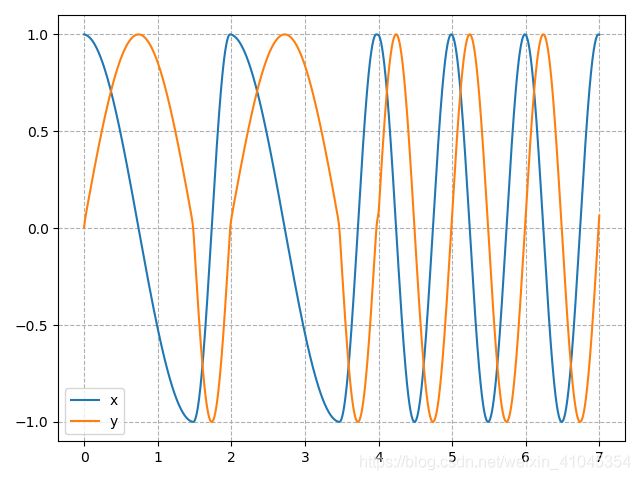
【CPG控制】Hopf振荡器引入beta参数
一、回顾
我们先来回顾一下hopf振荡器的最初形式:
d x d t = α ( μ − r 2 ) x − ω y \frac{dx}{dt} = \alpha(\mu - r^2)x - \omega y dtdx=α(μ−r2)x−ωy
d y d t = α ( μ − r 2 ) y + ω x \frac {dy}{dt} = \alpha(\mu-r^2)y+\omega x dtdy=α(μ−r2)y+ωx
在这微分方程组中,我们能够通过 α , μ , ω \alpha,\mu, \omega α,μ,ω三个参数来控制hopf振荡器的动态特性,分别对应收敛速度,幅值,以及周期,其具体公式如下:
- 幅值 A = μ A = \sqrt{\mu} A=μ
- 周期 T = 2 π ω T = \frac{2\pi}{\omega} T=ω2π
尽管通过震荡周期可以控制机器人的前进速度,通过幅值来控制关节的活动范围,但这对于我们的四足机器人来说,这可能远远不够用,因为我们可能需要改变机器人的运动步态来适应不同的地形,以及实现更低能耗的运作。
二、引入 β \beta β
首先我们来考虑不同的步态。尽管我们可以通过控制hopf振荡器之间的耦合关系来控制相位,但是如果不对hopf振荡器进行改进的话,就无法单独控制振荡器的输出信号的形状,即上升沿与下降沿所用的时间是一致的,是一个对称的信号。
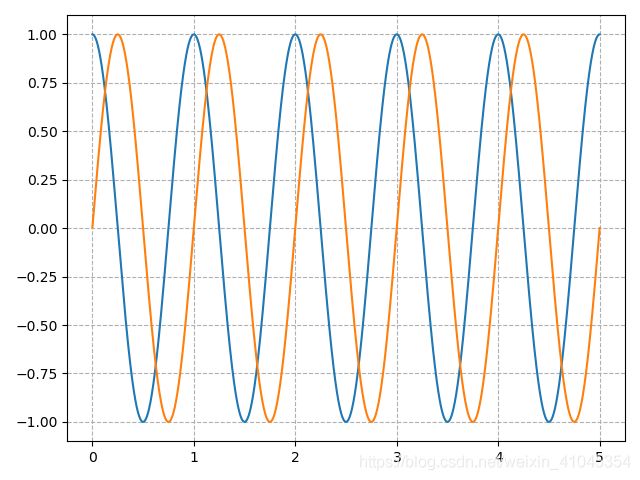
为了能够对这两者进行单独控制,使其能够适应不同负载因子下的运动模式,对 ω \omega ω进行以下改进,引入参数a(定值)和 β \beta β
{ ω = ω s t e − a y + 1 + ω s w e a y + 1 ω s t = 1 − β β ω s w \left\{\begin{matrix} \omega =& \frac{\omega_{st}}{e^{-ay}+1} + \frac{\omega_{sw}}{e^{ay}+1}\\ \\ \omega_{st} =& \frac{1-\beta}{\beta} \omega_{sw} \end{matrix}\right. ⎩⎨⎧ω=ωst=e−ay+1ωst+eay+1ωswβ1−βωsw
其中 ω s w , ω s t \omega_{sw}, \omega_{st} ωsw,ωst分别表示摆动相和支撑相的频率, β \beta β为负载因子,用于决定,摆动相和支撑相的比例关系,最终我们的模型如下:
d x d t = α ( μ − r 2 ) x − ω y d y d t = α ( μ − r 2 ) y + ω x r 2 = x 2 + y 2 ω = ω s t e − a y + 1 + ω s w e a y + 1 ω s t = 1 − β β ω s w \begin{matrix} \frac{dx}{dt}=& \alpha(\mu-r^2)x-\omega y\\ \\ \frac{dy}{dt}=& \alpha(\mu-r^2)y + \omega x\\ \\ r^2= & x^2 + y^2\\ \\ \omega=&\frac{\omega{st}}{e^{-ay}+1}+ \frac{\omega_{sw}}{e^{ay}+1} \\ \\ \omega_{st} =& \frac{1-\beta}{\beta}\omega_{sw} \end{matrix} dtdx=dtdy=r2=ω=ωst=α(μ−r2)x−ωyα(μ−r2)y+ωxx2+y2e−ay+1ωst+eay+1ωswβ1−βωsw
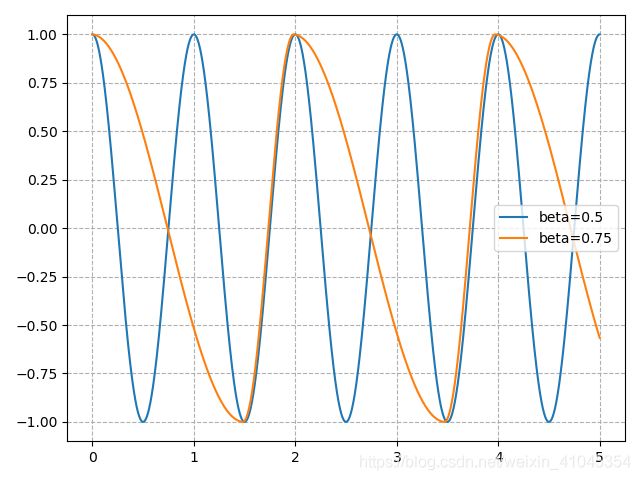
给定参数 α = 100 , μ = 1 , a = 50 \alpha=100, \mu=1, a=50 α=100,μ=1,a=50,分别取 β = 0.75 , 0.5 \beta=0.75,0.5 β=0.75,0.5,我们得到图像(x值曲线)
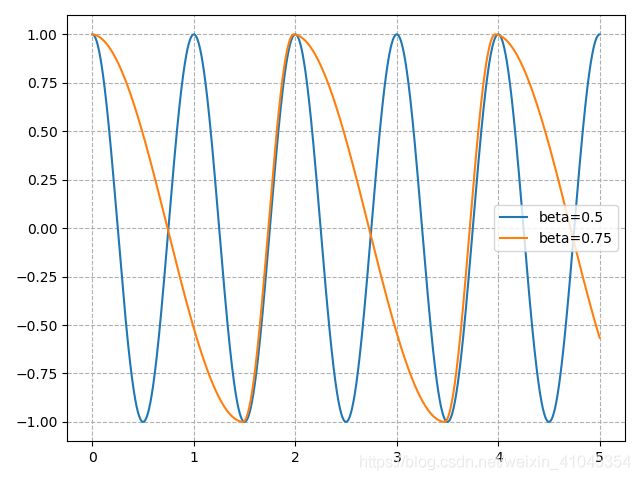
我们将其与 β = 0.5 \beta=0.5 β=0.5时的点运动放在一起,看下其点的运动变化:
三、 β \beta β连续变换
我们取不同的 β \beta β值能够得到不同形状的信号输出,如下图。
但是这是两条曲线,即在不同振荡器上实现。我们能否实现同个hopf振荡器上,信号输出的连续变化呢?答案是肯定的,而且,不需要修改我们的模型。如下图,振荡器在4s后, β \beta β从0.75连续变化成0.5。
如果 β \beta β不是连续变化的呢?(3s后突变),看下图可知,就会产生的信号就会不平滑。