材料力学-绪论

该系列讲解材料力学中的一些基础概念

一、变形

1、定义

构件受外力的作用，发成尺寸和形状的改变，这种变化称为形变

构件：工程结构或机械的零部件，其主要分类为：杆、板、壳、块

2、分类

材料力学中的变形主要分为以下两种类型：

• 弹性变形：能够随着外力的撤去而消失的变形，例如金属等韧性较高的材料
• 塑性变形：在外力去掉之后保留下来的变形，例如橡皮泥等可塑性较高的材料

在工程实践中，绝大多数构件的变形都被限制在弹性范围内，即能够保持原有尺寸和形状

二、构件承载能力

我们在工程中选择材料时，通常需要考虑以下三个方面

1、强度要求

构件应具有足够的抵抗破坏的能力，即在收到零部件收到外力冲击时，能够保证自身结构不被破坏，例如产生断裂

2、刚度要求

构件应具有足够的抵抗变形的能力，即在收到零部件收到外力冲击时，能够保证自身变形在允许的范围之内

3、稳定性要求

构件应具有足够的抵抗失稳的能力

三、材料力学中的基本假设

材料力学将构件视为变形固体，基于此，作出以下三个假设：

• 连续性假设：认为组成物体的物质毫无间隙的填满物体的整个几何空间

• 均匀性假设：认为物体内各点出的力学性能是相同的

• 各向同性假设：认为物体沿不同方向具有相同的力学性能

四、杆件的基本变形形式

第一节介绍了构件的定义以及分类，现在我们来看构件的第一种形式，杆件

1、杆件的几何因素及分类

• 轴线
• 横截面

2、杆件的分类

• 直杆，等直杆
• 曲杆

3、杆件的四种变形形式

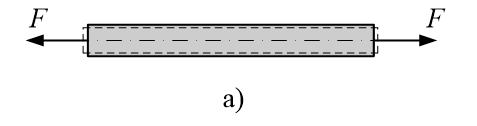
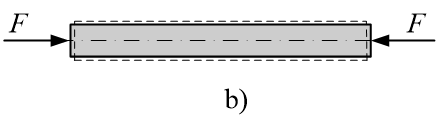
a、拉伸或压缩：在一对大小相等，方向相反，作用线与轴线重合的外力作用下，杆件的主要变形是长度的改变

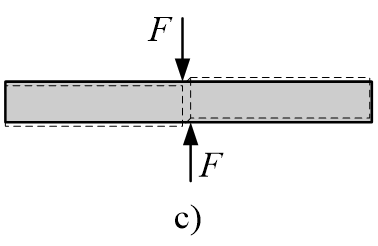
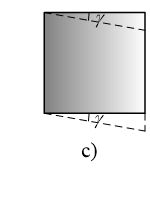
b、剪切：在一对大小相等，方向相反，作用线相距很近的横向力作用下，杆件的横截面将沿外力作用方向发生相对错动

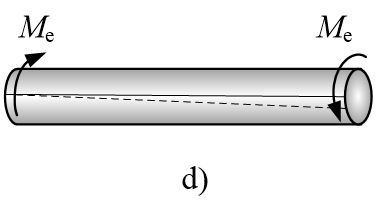
c、扭转：在一对大小相等，转向相反，作用面垂直于杆轴线的两个力偶作用下，杆件的任意两横截面绕轴线发生相对转动

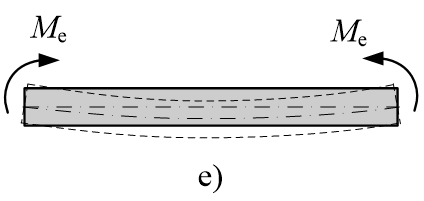
d、弯曲：在一对大小相等，转向相反，作用面位于包含杆轴线的纵向平面内的力偶作用下，杆件的轴线变为曲线

五、内力，截面法

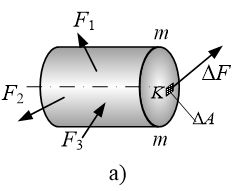
1、内力的概念

杆件内各部相连部分之间产生的相互作用力

2、内力的计算

• a、假想截开
  
• b、内力代替
  
• c、向形心简化
  

将主矢$F_R$和主矩$M_C$沿坐标轴分解，其中

• $F_N$为轴力
• $F_{sy}，F_{sz}$为剪力
• $M_x$为扭矩
• $M_y,M_z$为弯矩

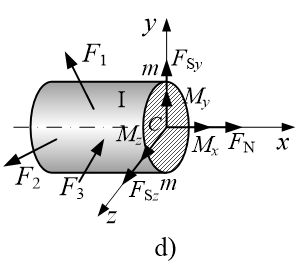
d、平衡求解
$$\begin{array}{ccc}\sum F_x=0& \sum F_y=0& \sum F_z=0\\ & & \\ \sum M_x=0& \sum M_y=0& \sum M_z=0\end{array}$$

这种根据隔离体的平衡条件，由外力确定内力的方法称为截面法

六、应力-内力的集中分布

平均应力：$$\bar{p}=\frac{\Delta f}{\Delta A}$$

点K处的应力：$$p=\underset{\Delta A\to 0}{\lim }\frac{\Delta f}{\Delta A}$$

将应力沿截面分解

得到两个应力分量，

• 法向应力分量，称为正应力，用$\sigma$表示
• 切向应力分量，称为切应力，用$\tau$表示

两者有以下关系
$$p^2={\sigma }^2+{\tau }^2$$

应力单位：帕（Pa），1Mpa = $10^6$Pa，1Gpa = $10^9$Pa

七、应变

围绕一点去微笑的正六面体，称为单元体

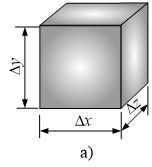
1、棱边长度的改变

$\Delta x$范围内的单位变形量：$\frac{\Delta u}{\Delta x}$

该点处沿x方向的线应变：${\epsilon }_x=\underset{\Delta x\to 0}{\lim }\frac{\Delta u}{\Delta x}$

2、棱边间夹角的改变

直角的改变量$\gamma$称为切应变,单位为rad