数据在内存中的存储总结

数据类型介绍：

基本内置类型分别为：

char         //字符数据类型
short        //短整型
int          //整形
long         //长整型
long long    //更长的整形
float        //单精度浮点数
double       //双精度浮点型

//注意： C语言中没有字符串类型

 

类型的意义：

1. 使用这个类型开辟的内存空间大小（大小决定了适用范围）。

2. 如何看待内存空间的视角。

在32位平台下，任何指针类型都只占4个字节。

 

类型的归类：

整形家族：

char 
        unsigned char
        signed char

short
        unsigned short [int]
        signed short [int]

int
        unsigned int
        signed int

long
        unsigned long [int]
        signed long [int]

浮点数家族：

float

double

构造类型：

> 数组类型

> 结构体类型 struct

> 枚举类型 enum

> 联合类型 union

指针类型 空类型：

void 表示空类型（无类型）通常应用于函数的返回类型、函数的参数、指针类型。

注意：

1. void 是类型，不能定义变量，空类型对应的大小是0,。所以 void 无法开辟空间，即无法定义变量。

2. 虽然 void 在linux 系统下大小为 1 个字节，但是系统认定 void 为空类型，同样无法定义变量。

3. 虽然 void 不能定义变量，但是 void* 可以，在 32 为平台下，任何指针的大小都是4个字节，但是不能解引用。

4. C 语言中函数的返回值类型可以省略，但是省略之后默认为 int。

5. void* 可以接收任何类型。

 

 整形在内存中的存储：

一个变量创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。

在知道整形怎么存储之前，我们先引入

原码、反码、补码。

计算机中的符号数有三种表示方法，即原码、反码和补码。三种方法均有符号位和数值位两部分，符号位 0 表示正数， 符号位 1 表示负数，而数值位，三种表示方法各不相同。
 

原码：直接将二进制按照正负数的形式翻译成二进制就可以了。

反码：将原码的符号位不变，其他位依次按位取反就可以得到了。

补码：反码 +1 就得到补码。

正数的原码、反码、补码相同。  

对整形来说：数据存放内存中其实存放的是补码。

这样也是有原因的：

1. 使用补码，可以将符号位和数值域统一处理；

2. 加法和减法也可以统一处理（CPU只有加法器）；

3. 补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

先来看看整形在内存中存储的例子：

我们先定义两个变量：

int a = 20;
int b = -10;

然后看看他们在内存中是如何存的。

变量a在内存中的存储：

因为a为正数，所以在存储的时候先将十进制数，转化为二进制数原码，并且因为是正数，所以原、反、补码相同，不用转化。

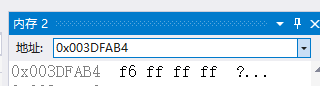
变量b在内存中的存储：

因为b为负数，在进行十进制转化为二进制原码后，要进行原码和补码之间的转化，转化过程为符号位不变其他位按位取反，再加一。

可是有没有觉得怪怪的？为什么数字是反过来排列的？难道不是应该是 00 00 00 14 和 ff ff ff f6 吗？

这里就要引入小端存储和大端存储。

数据是有高、低位之分的，内存地址是有高、低地址之别的。

小端存储模式：是指数据的低位保存在内存的低地址中；

上图就是小端存储，存储的方式是

 

 

大端存储模式：是指数据的低位保存在内存的高地址中。

与小端存储一样，只是反过来，将低位数据保存在高地址中，这里不再赘言。

 

浮点数在内存中的存储：
 

我们先看一个列子：

int main(void)
{

	int n = 9;
	float *pFloat = (float *)&n;
	printf("n -> %d\n", n);
	printf("pFloat -> %f\n", *pFloat);

	*pFloat = 9.0;
	printf("n -> %d\n", n);
	printf("pFloat -> %f\n", *pFloat);
    
        system("pause");
	return 0;
}

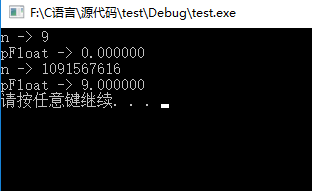
这个程序的输出是：

为什么呢？？？？？？

只要我们了解了浮点数在内存中是如何存储的，这个问题就很好解决！

1. 根据国际标准IEEE 754，任意一个二进制浮点数V可以表示成下面的形式：
 ·  (-1)^S * M * 2^E。

 ·  (-1)^S 表示符号位，当S == 0, V为正数；当S == 1, V为负数。

 ·  M表示有效数字，大于等于1，小于2、

 ·  2^E表示指数位。

举个例子：十进制的5.0，转化成二进制就变成了101.0，用科学计数法表示就是 1.01 * 2^2 。那么，按照上面V的格式，可以得出S = 0， M = 1.01，E = 2 。

                  如果是-5.0，S = 1， M = 1.01， E = 2 。

2. IEEE 754规定：对于32位浮点数，最高的1位是符号位S， 接着的8位是指数E,剩下的23位为有效数字M。

E和M的存储方式也是IEEE 754的规定，记住就好。

对于64位浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

图跟上图32位类似，这里就不画了。

E的两种特殊取值：

1. E全为0：

    当E全为0的时候，即2的次方为0 - 127 为2^-127次方，所以，当s = 0时，一个正数的2^-127次方，是一个从数轴的右边无线趋近于0的数字；而当s = 1时，一个负数的2^-127次方是从数轴左边无线趋近于0的数字。

    所以当E全为0的时候，实际就表示的是+-0，所以浮点数不可以在程序中出现 与0去比较（浮点数 == 0），而是要跟一段范围去比较。

2. E全为1：

    当E全为1的时候（如果M全为0），即2的次方255 - 127 = 128，所以当S = 0时，表示1 * 2^128次方，当s = 1时表示-1*2^128次方。

    所以当E全为1时，其实表示的就是这个浮点数的取值范围。

 

那么我们回到上面的例题，

1. n = 9 的存储方式是

    0000 0000 0000 0000 0000 0000 0000 1001

    float *pFloat = (float *)&n   将n强制类型转换为float形

    系统就是认为上面的存储方式是浮点数的存储方式

    即1.00000000000000000001001*2^-127

    是一个及其接近0的数字，所以打印0

2. 第二种输入方法一样，给指针赋值9.0，指针是浮点型，

    所以系统按照浮点数的存储方式存放这个数字，

    n为整形，系统输出n的时候按照整形的在内存中的存储方式去读，

    所以输出n为一个非常大的数字。

这里在普及一下，强制类型转换，并没有改变什么，只是改变了系统读取这个二进制数的方式。

END……