Cocos2d-x教程(33)-三维物体AABB碰撞检测算法
欢迎加入Cocos2d-x 交流群:193411763
转载时请注明原文出处 :http://blog.csdn.net/u012945598/article/details/39524343
-----------------------------------------------------------------------------------------------------------------------------------------------------------
在Cocos2d-x 3.x版本添加了对3D物体的支持后,3D物体的碰撞检测方法也随之更新,其中一种最简单的碰撞检测方法就是AABB碰撞检测。
1. AABB包围盒
在游戏中,为了简化物体之间的碰撞检测运算,通常会对物体创建一个规则的几何外形将其包围。
其中,AABB(axis-aligned bounding box)包围盒被称为轴对其包围盒。
二维场景中的AABB包围盒具备特点:(注:由于Cocos2d-x是基于Opengl ES的,所以下图中的所有坐标系均采用右手直角坐标系)
(1) 表现形式为四边形,即用四边形包围物体。
(2) 四边形的每一条边,都会与坐标系的轴垂直。
如图 1-1 所示:
图1-1
三维场景中的AABB包围盒特点:
(1) 表现形式为六面体。
(2) 六面体中的每条边都平行于一个坐标平面。
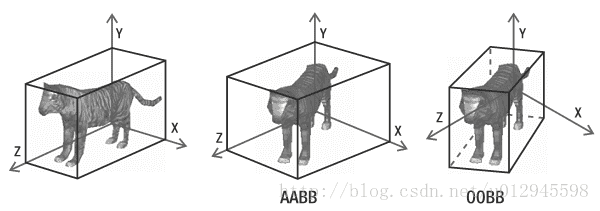
如图 1-2 所示:
图 1-2(图片来源百度)
在图1-2中,为了更明显的展示AABB包围盒的特点,在最右侧展示了一个OBB(Oriented Bounding Box)包围盒,也称作有向包围盒。
可以看出,AABB包围盒与OBB包围盒的最直接的区别就是,AABB包围盒是不可以旋转的,而OBB包围盒是可以旋转的,也就是有向的。
2. 二维场景中的AABB碰撞检测原理
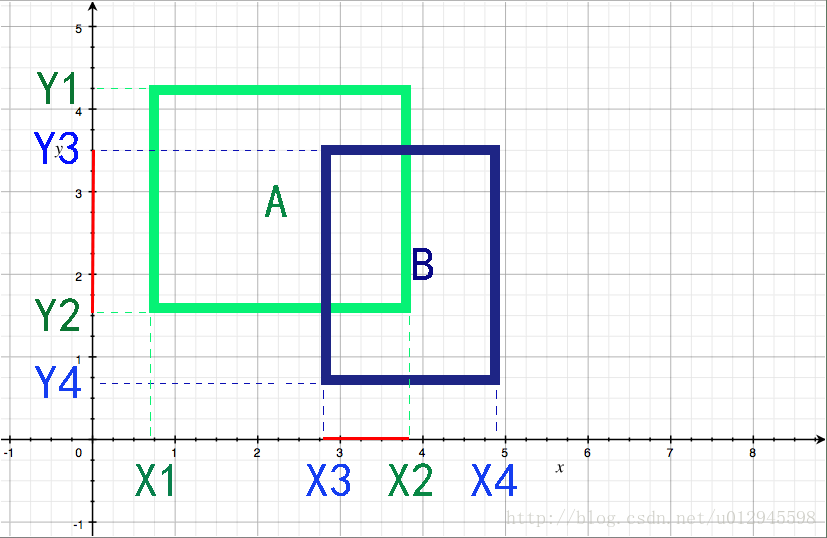
首先来看一张二维场景中的物体碰撞图:图 2-1
在图 2-1中,分别做物体A与物体B在X,Y轴方向的投影,物体A的Y轴方向最大点坐标为Y1,最小点坐标Y2,X轴方向最小点坐标X1,最大点坐标X2,物体B同理。
图中红色区域为物体A与物体B投影的重叠部分。
可以看出,AABB碰撞检测具有如下规则:
物体A与物体B分别沿两个坐标轴做投影,只有在两个坐标轴都发生重叠的情况下,两个物体才意味着发生了碰撞。
所以,在程序中做二维游戏的AABB碰撞检测时,只需验证物体A与物体B是否满足如下条件:
(1)物体A的Y轴方向最小值大于物体B的Y轴方向最大值;
(2)物体A的X轴方向最小值大于物体B的X轴方向最大值;
(3)物体B的Y轴方向最小值大于物体A的Y轴方向最大值;
(4)物体B的X轴方向最小值大于物体A的X轴方向最大值;
若满足上述条件,则证明物体A与物体B并未发生重合,反之,则证明物体A与物体B重合。
3. 三维场景中的AABB碰撞检测原理
首先,再来看一下图2-1中的二维物体A和物体B的包围盒,可以发现实际上判断物体A与物体B是否发生重合只需要知道两个信息:(1) 物体A的最小点的信息,即图2-1中A的左下角点;以及物体A的最大点的信息,即图2-1中A的右上角点。
(2) 物体B的最小点的信息,物体B的最大点的信息。
也就是说在二维场景的碰撞检测中,每个物体的顶点坐标信息都可以由两个坐标来确定,即两个坐标就可以标识一个物体了,所以两个物体的碰撞检测只需要获得到四个点坐标就可以了。
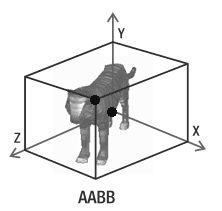
之前在图1-2中已经看到,三维场景中物体的AABB包围盒是一个六面体,其坐标系对于二维坐标系来讲只是多了一个Z轴,所以实际上在三维场景中物体的AABB碰撞检测依然可以采用四个点信息的判定来实现。即从物体A的八个顶点与物体B的八个顶点分别选出两个最大与最小的顶点进行对比。三维物体的AABB包围盒的八个顶点依旧可以用两个顶点来标识,如图 3-1 所示:
图3-1
只要确定了图中黑色点部分的坐标,就可以确定八个顶点的全部信息了。
在Cocos2d-x 3.x版本中,为开发者提供了AABB类,用于保存包围盒的最大顶点与最小顶点的信息,并且为每个Sprite3D对象提供了获取AABB包围盒的接口,在AABB类同时提供了判断相应的碰撞检测的方法。有一点需要注意的是,CCAABB类中一开始保存的最大顶点与最小顶点的信息实际上是物体坐标系中的信息,而实际上在碰撞检测时需要将其转换成世界坐标系中的点,这一过程在Sprite3D中的getAABB()方法中实现,可通过CCAABB中的
transform()方法来完成。
下面对AABB的源码进行分析:
CCAABB.h 文件
class CC_3D_DLL AABB
{
public:
/**
* 构造函数
*/
AABB();
/**
* 构造函数 参数:最小顶点坐标,最大顶点坐标
*/
AABB(const Vec3& min, const Vec3& max);
/**
* 构造函数 参数:AABB包围盒
*/
AABB(const AABB& box);
/**
* 获取包围盒中心点坐标
*/
Vec3 getCenter();
/* 获取包围盒八个顶点信息
* Z轴正方向的面
* verts[0] : 左上顶点
* verts[1] : 左下顶点
* verts[2] : 右下顶点
* verts[3] : 右上顶点
*
* Z轴负方向的面
* verts[4] : 右上顶点
* verts[5] : 右下顶点
* verts[6] : 左下顶点
* verts[7] : 左上顶点
*/
void getCorners(Vec3 *dst) const;
/**
* 判断两个包围盒是否重合
*/
bool intersects(const AABB& aabb) const;
/**
* 判断一个点是否在包围盒内
*/
bool containPoint(const Vec3& point) const;
/**
由两个包围盒生成一个能同时包围这两个包围盒的最小包围盒
*/
void merge(const AABB& box);
/**
* 设置包围盒的最大顶点与最小顶点
*/
void set(const Vec3& min, const Vec3& max);
/**
* 复位函数 初始化最大最小顶点信息
*/
void reset();
bool isEmpty() const;
/**
* 更新最大顶点与最小顶点信息
*/
void updateMinMax(const Vec3* point, ssize_t num);
/**
* 由一个矩阵对对包围盒进行顶点变换
*/
void transform(const Mat4& mat);
public:
Vec3 _min; //三维向量 保存最小点坐标
Vec3 _max; //三维向量 保存最大点坐标
};
NS_CC_END
#include "3d/CCAABB.h"
NS_CC_BEGIN
//构造函数
AABB::AABB()
{
reset(); //初始化最大顶点与最小顶点
}
AABB::AABB(const Vec3& min, const Vec3& max)
{
set(min, max); //设置最大顶点与最小顶点
}
AABB::AABB(const AABB& box)
{
set(box._min,box._max); //设置最大顶点与最小顶点
}
//获取包围盒中心点坐标
Vec3 AABB::getCenter()
{
Vec3 center;
center.x = 0.5f*(_min.x+_max.x);
center.y = 0.5f*(_min.y+_max.y);
center.z = 0.5f*(_min.z+_max.z);
return center;
}
//获取包围盒八个顶点信息
void AABB::getCorners(Vec3 *dst) const
{
assert(dst);
// 朝着Z轴正方向的面
// 左上顶点坐标
dst[0].set(_min.x, _max.y, _max.z);
// 左下顶点坐标
dst[1].set(_min.x, _min.y, _max.z);
// 右下顶点坐标
dst[2].set(_max.x, _min.y, _max.z);
// 右上顶点坐标
dst[3].set(_max.x, _max.y, _max.z);
// 朝着Z轴负方向的面
// 右上顶点坐标
dst[4].set(_max.x, _max.y, _min.z);
// 右下顶点坐标
dst[5].set(_max.x, _min.y, _min.z);
// 左下顶点坐标
dst[6].set(_min.x, _min.y, _min.z);
// 左上顶点坐标
dst[7].set(_min.x, _max.y, _min.z);
}
//判断两个包围盒是否碰撞
bool AABB::intersects(const AABB& aabb) const
{
return ((_min.x >= aabb._min.x && _min.x <= aabb._max.x) || (aabb._min.x >= _min.x && aabb._min.x <= _max.x)) &&
((_min.y >= aabb._min.y && _min.y <= aabb._max.y) || (aabb._min.y >= _min.y && aabb._min.y <= _max.y)) &&
((_min.z >= aabb._min.z && _min.z <= aabb._max.z) || (aabb._min.z >= _min.z && aabb._min.z <= _max.z));
}
//判断点和包围盒是否碰撞
bool AABB::containPoint(const Vec3& point) const
{
if (point.x < _min.x) return false;
if (point.y < _min.y) return false;
if (point.z < _min.z) return false;
if (point.x > _max.x) return false;
if (point.y > _max.y) return false;
if (point.z > _max.z) return false;
return true;
}
//生成一个新的包围盒 同时容纳两个包围盒
void AABB::merge(const AABB& box)
{
// 计算新的最小点坐标
_min.x = std::min(_min.x, box._min.x);
_min.y = std::min(_min.y, box._min.y);
_min.z = std::min(_min.z, box._min.z);
// 计算新的最大点坐标
_max.x = std::max(_max.x, box._max.x);
_max.y = std::max(_max.y, box._max.y);
_max.z = std::max(_max.z, box._max.z);
}
//设置最大顶点与最小顶点
void AABB::set(const Vec3& min, const Vec3& max)
{
this->_min = min;
this->_max = max;
}
//顶点复位 初始化信息
void AABB::reset()
{
_min.set(99999.0f, 99999.0f, 99999.0f);
_max.set(-99999.0f, -99999.0f, -99999.0f);
}
//检测坐标信息是否有误
bool AABB::isEmpty() const
{
return _min.x > _max.x || _min.y > _max.y || _min.z > _max.z;
}
//由给定点坐标点重新确定最大最小的坐标向量
void AABB::updateMinMax(const Vec3* point, ssize_t num)
{
for (ssize_t i = 0; i < num; i++)
{
// 最小x坐标
if (point[i].x < _min.x)
_min.x = point[i].x;
// 最小y坐标
if (point[i].y < _min.y)
_min.y = point[i].y;
// 最小z坐标
if (point[i].z < _min.z)
_min.z = point[i].z;
// 最大x坐标
if (point[i].x > _max.x)
_max.x = point[i].x;
// 最大y坐标
if (point[i].y > _max.y)
_max.y = point[i].y;
// 最大z坐标
if (point[i].z > _max.z)
_max.z = point[i].z;
}
}
//通过给定的变换矩阵对包围盒进行变换
void AABB::transform(const Mat4& mat)
{
Vec3 corners[8]; //保存包围盒八个顶点
//朝向z轴正方向的面
//左上顶点坐标
corners[0].set(_min.x, _max.y, _max.z);
//左下顶点坐标
corners[1].set(_min.x, _min.y, _max.z);
//右下顶点坐标
corners[2].set(_max.x, _min.y, _max.z);
//右上顶点坐标
corners[3].set(_max.x, _max.y, _max.z);
//朝向z轴负方向的面
//右上顶点坐标
corners[4].set(_max.x, _max.y, _min.z);
//右下顶点坐标
corners[5].set(_max.x, _min.y, _min.z);
//左下顶点坐标
corners[6].set(_min.x, _min.y, _min.z);
//左上顶点坐标
corners[7].set(_min.x, _max.y, _min.z);
//顶点变换
for (int i = 0; i < 8; i++)
mat.transformPoint(&corners[i]);
//复位最大顶点最小顶点
reset();
//重新计算最大最小点信息
updateMinMax(corners, 8);
}
NS_CC_END
4. 总结
图 4-1