随机森林在sklearn中的实现和调参

集成算法的概述

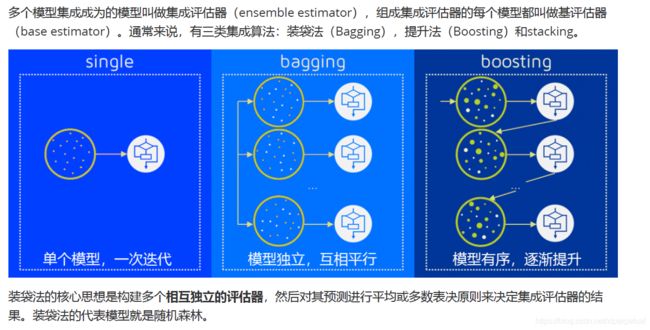
集成算法会考虑多个评估器的建模结果，汇总之后得到一个结果，以此来获取比单个模型更好的回归或分类表现。

随机深林是袋装法的代表模型

RandomForestClassifier分类树

RandomForestClassifier类
随机森林分类器
sklearn.ensemble.RandomForestClassifier
参数
决策树中遇到过的参数

其他参数
n_estimators
越大，模型的效果往往越好。
一般0~200之间比较好

还是用sklearn.datasets里的红酒数据集，先用train_test_split来划分测试集和训练集，方法如下`

from sklearn.model_selection import train_test_split

Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
#首先先分训练集和测试集，用train_test_split来划分
#实例化
clf = DecisionTreeClassifier(random_state=0)
rfc = RandomForestClassifier(random_state=0)
# 把训练集带入实例化后的模型进行训练，使用的接口是fit
clf = clf.fit(Xtrain,Ytrain)
rfc = rfc.fit(Xtrain,Ytrain)
# 使用score接口将测试集导入我们训练好的模型，去获取我们希望获取的结果（score,Y_test）
score_c = clf.score(Xtest,Ytest)
score_r = rfc.score(Xtest,Ytest)
print("Single Tree:{}".format(score_c)
      ,"Random Forest:{}".format(score_r)
     )

代码结果为：
Single Tree:0.9444444444444444
Random Forest:0.9629629629629629

可以看出来好像随机森林比决策树的分类结果要好一点。
如果不信的话可以用交叉验证（cross_val_score）来验证一下

#交叉验证：cross_val_score
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt

rfc = RandomForestClassifier(n_estimators = 25)
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10)
clf = DecisionTreeClassifier()
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10)

plt.plot(range(1,11),rfc_s,label="Random Forest")
plt.plot(range(1,11),clf_s,label="Single Tree")
plt.legend()
plt.show()

代码结果

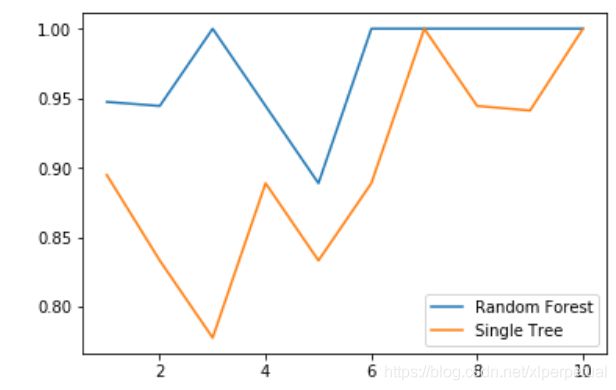
可以看出来随机森林的效果比单个决策树，整体上都要好很多！
你要是还不信的话，我们跑100次试一下，其中每10次我们取个平均值，做个图看一下！

rfc_1 = []
clf_1 = []

for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    rfc_1.append(rfc_s)
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()
    clf_1.append(clf_s)
plt.plot(range(1,11),rfc_1,label="Random Forest")
plt.plot(range(1,11),clf_1,label="Decision Tree")
plt.legend()
plt.show()

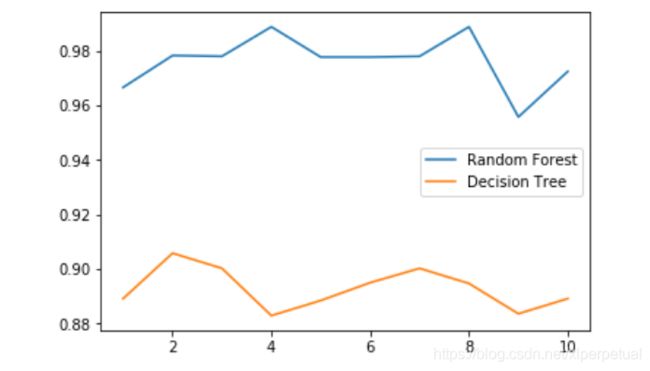
这样是不是很明显了！
随机森林的score整体要比决策树强一个档次！

接下来，我们看一下n_estimators的学习曲线
（这段代码要跑两分钟左右！）

supera = []
for i in range(200):
    rfc = RandomForestClassifier(n_estimators=i+1,n_jobs=-1)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    supera.append(rfc_s)
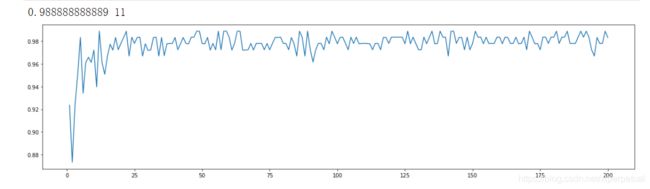
print(max(supera),supera.index(max(supera)))
plt.figure(figsize=[20,5])
plt.plot(range(1,201),supera)
plt.show()

从结果可以看出，n_estimators取11时，随机森林的score是最高的，为0.98888…。

random_state
随机森林的本质是一种装袋集成算法（bagging），装袋集成算法是对基评估器的预测结果进行平均或用多数表决
原则来决定集成评估器的结果。在刚才的红酒例子中，我们建立了25棵树，对任何一个样本而言，平均或多数表决
原则下，当且仅当有13棵以上的树判断错误的时候，随机森林才会判断错误。单独一棵决策树对红酒数据集的分类
准确率在0.85上下浮动，假设一棵树判断错误的可能性为0.2(ε)，那20棵树以上都判断错误的可能性是：

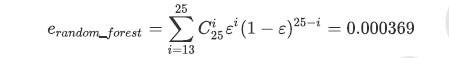
import numpy as np
from scipy.special import comb
# scipy库
# 假设一棵树判断错误的可能性为0.2，那20棵树以上都判断错误的可能性是
np.array([comb(25,i)*(0.2**i)*((1-0.2)**(25-i)) for i in range(13,26)]).sum()
#可以看出随机森林比单个决策树的效果要好很多

代码结果为
0.00036904803455582827（这是发生错误的概率）

rfc = RandomForestClassifier(n_estimators = 25, random_state=20)
rfc = rfc.fit(Xtrain,Ytrain)
for i in range(len(rfc.estimators_)):
    print(rfc.estimators_[i].random_state)
# 可以看出利用random_state生成的森林是固定的，但是森林里每一个树对应的random_state是不同的

378518883
1663920602
1708167439
1951685855
1681611676
1942519002
1356511625
521790868
154144587
602822422
823592519
1934675106
1626422240
742452342
79503912
176838101
678396378
1467049754
832580347
1359590355
1169590032
1213377277
938905318
1010465510
1215491262

bootstrap & oob_score
bootstrap参数默认True，代表采用这种有放回的随机抽样技术。

在一个含有n个样本的原始训练集中，我们进行随机采样，每次采样一个样本，并在抽取下一个样本之前将该样本放回原始训练集，也就是说下次采样时这个样本依然可能被采集到，这样采集n次，**最终得到一个和原始训练集一样大的，n个样本组成的自助集。**由于是随机采样，这样每次的自助集和原始数据集不同，和其他的采样集也是不同的。这样我们就可以自由创造取之不尽用之不竭，并且互不相同的自助集，用这些自助集来训练我们的基分类器，我们的基分类器自然也就各不相同了。

然而有放回抽样也会有自己的问题。由于是有放回，一些样本可能在同一个自助集中出现多次，而其他一些却可能被忽略，一般来说，自助集大约平均会包含63%的原始数据。而有放回抽样也会有自己的问题。由于是有放回，一些样本可能在同一个自助集中出现多次，而其他一些却可能被忽略，一般来说，自助集大约平均会包含63%的原始数据。因为每一个样本被抽到某个自助集中的概率为：当n足够大时，这个概率收敛于1-(1/e)，约等于0.632。**因此，会有约37%的训练数据被浪费掉，没有参与建模，这些数据被称为袋外数据(out of bag data，简写为oob)。**除了我们最开始就划分好的测试集之外，这些数据也可以被用来作为集成算法的测试集。也就是说，在使用随机森林时，我们可以不划分测试集和训练集，只需要用袋外数据来测试我们的模型即可。当然，这也不是绝对的，当n和n_estimators都不够大的时候，很可能就没有数据掉落在袋外，自然也就无法使用oob数据来测试模型了。

# 无需划分训练集和测试集,使用袋外数据
rfc = RandomForestClassifier(n_estimators=25,oob_score=True)
rfc = rfc.fit(wine.data,wine.target)

采用以上代码来采用袋外数据

其他重要属性和接口
属性
feature_importances_

rfc.feature_importances_
[*zip(feature_name,clf.feature_importances_)]
# 可以用zip来将特征的重要度和特征名称一一对应

四个常用接口
apply：输入测试集，返回测试集每一个样本在树中每一个叶子节点的索引
fit
predict：输入测试集，返回对测试集预测的标签
score
其他接口
predict_proba:每一个样本对应分配到的每一个标签的概率

rfc.predict_proba(Xtest)

代码结果
array([[ 0. , 1. , 0. ],
[ 0. , 1. , 0. ],
[ 0.04, 0.08, 0.88],
[ 0. , 0.04, 0.96],
[ 1. , 0. , 0. ],
[ 1. , 0. , 0. ],
[ 0.04, 0.92, 0.04],
[ 0.8 , 0.2 , 0. ],
[ 0. , 0.08, 0.92],
[ 0. , 0.96, 0.04],
[ 0.92, 0.08, 0. ],
[ 0. , 1. , 0. ],
[ 0. , 0. , 1. ],
[ 0.2 , 0.8 , 0. ],
[ 0.76, 0.24, 0. ],
[ 0. , 1. , 0. ],
[ 0. , 0.04, 0.96],
[ 1. , 0. , 0. ],
[ 0. , 1. , 0. ],
[ 0. , 1. , 0. ],
[ 0. , 0.96, 0.04],
[ 0.12, 0.84, 0.04],
[ 0.08, 0.84, 0.08],
[ 0. , 1. , 0. ],
[ 1. , 0. , 0. ],
[ 1. , 0. , 0. ],
[ 0.04, 0.04, 0.92],
[ 1. , 0. , 0. ],
[ 0. , 1. , 0. ],
[ 1. , 0. , 0. ],
[ 0.96, 0.04, 0. ],
[ 0. , 1. , 0. ],
[ 1. , 0. , 0. ],
[ 1. , 0. , 0. ],
[ 0.04, 0.96, 0. ],
[ 1. , 0. , 0. ],
[ 0.96, 0.04, 0. ],
[ 1. , 0. , 0. ],
[ 0.04, 0.84, 0.12],
[ 0. , 0. , 1. ],
[ 0. , 1. , 0. ],
[ 1. , 0. , 0. ],
[ 1. , 0. , 0. ],
[ 0.96, 0. , 0.04],
[ 0.92, 0.08, 0. ],
[ 0. , 1. , 0. ],
[ 0. , 1. , 0. ],
[ 0. , 1. , 0. ],
[ 0. , 1. , 0. ],
[ 0.84, 0.16, 0. ],
[ 0. , 0.08, 0.92],
[ 0. , 0.08, 0.92],
[ 0. , 0. , 1. ],
[ 0. , 0.88, 0.12]])
与predict的结果对比。
array([1, 1, 2, 2, 0, 0, 1, 0, 2, 1, 0, 1, 2, 1, 0, 1, 2, 0, 1, 1, 1, 1, 1,
1, 0, 0, 2, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 2, 1, 0, 0, 0, 0, 1,
1, 1, 1, 0, 2, 2, 2, 1])
所有的参数，属性与接口，全部和随机森林回归器一致。仅有的不同就是回归树与分类树的不同，不纯度指标，参数criterion不一致。

RandomForestRegressor回归树

重要的参数，属性和接口

criterion

回归树衡量分枝质量的指标
1.输入“mse”使用均方误差mean squared error(MSE)
2.输入“friedman_mse”使用费尔德曼均方误差
3.输入“mae”使用绝对平均误差MAE（mean absolute error）
在回归树中，MSE不只是我们的分枝质量衡量指标，也是我们最常用的衡量回归树回归质量的指标，在回归中，我们追求的是，MSE越小越好。

最重要的属性和接口，都与随机森林的分类器相一致，还是apply, fit, predict和score最为核心。值得一提的是，随
机森林回归并没有predict_proba这个接口，因为对于回归来说，并不存在一个样本要被分到某个类别的概率问
题，因此没有predict_proba这个接口。

from sklearn.datasets import load_boston  # 一个标签是连续性变量的数据集
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestRegressor
#实例化
regressor = RandomForestRegressor(n_estimators = 100, random_state = 0)
cross_val_score(regressor,boston.data,boston.target,cv=10
               ,scoring = "neg_mean_squared_error")

进行十次交叉验证，采用neg_mean_squared_error（负的均方误差）来进行打分。结果如下：
array([-10.60400153, -5.34859049, -5.00482902,-21.30948927,-12.21354202, -18.50599124, -6.89427068, -93.92849386,-29.91458572, -15.1764633 ])
那么除了neg_mean_squared_error这个模型评估指标以外，sklearn还有哪些指标呢？
我们用下面这个代码，查看一下：

import sklearn
# sklearn当中的模型评估指标（打分）列表
sorted(sklearn.metrics.SCORERS.keys())

[‘accuracy’,
‘adjusted_mutual_info_score’,
‘adjusted_rand_score’,
‘average_precision’,
‘completeness_score’,
‘explained_variance’,
‘f1’,
‘f1_macro’,
‘f1_micro’,
‘f1_samples’,
‘f1_weighted’,
‘fowlkes_mallows_score’,
‘homogeneity_score’,
‘log_loss’,
‘mean_absolute_error’,
‘mean_squared_error’,
‘median_absolute_error’,
‘mutual_info_score’,
‘neg_log_loss’,
‘neg_mean_absolute_error’,
‘neg_mean_squared_error’,
‘neg_mean_squared_log_error’,
‘neg_median_absolute_error’,
‘normalized_mutual_info_score’,
‘precision’,
‘precision_macro’,
‘precision_micro’,
‘precision_samples’,
‘precision_weighted’,
‘r2’,
‘recall’,
‘recall_macro’,
‘recall_micro’,
‘recall_samples’,
‘recall_weighted’,
‘roc_auc’,
‘v_measure_score’]
有点点多哈!