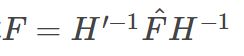计算机视觉——对极几何与基础矩阵

1、对极几何

对极几何是研究两幅图像之间存在的几何。它和场景结构无关，只依赖于摄像机的内外参数。研究这种几何可以用在图像匹配、三维重建方面。

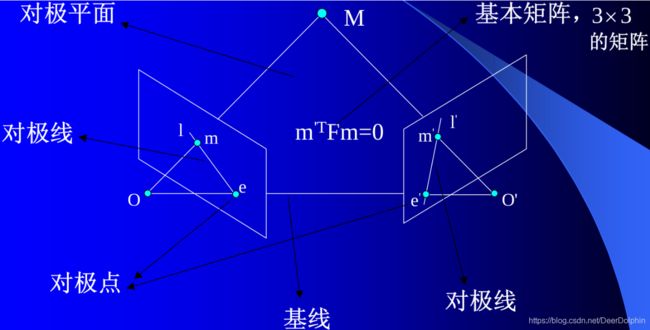
• 基线：连接两个摄像机光心$$O(O^{\prime })$$的直线
• 对极点：基线与像平面的交点
• 对极平面：过基线的平面
• 对极线：对极平面与图像平面的交线
• 基本矩阵F：对应点对之间的约束$$m^{\prime T}{F}^{\prime }m=0$$

1.1 极线约束

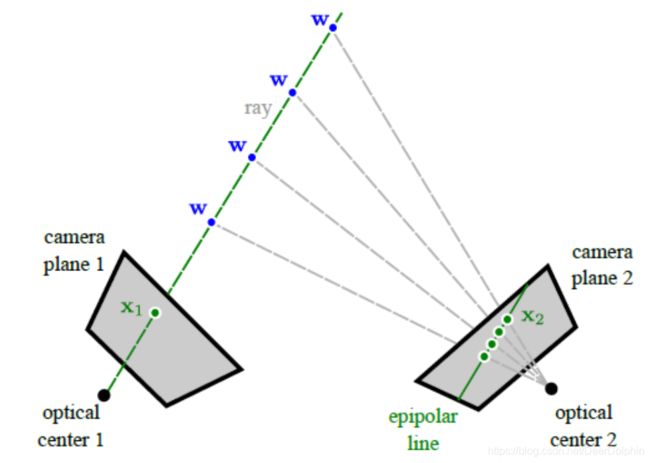
　　从第一个摄像机可得知，该点必定位于3D空间中的一条特定光线上。进而第二幅图像中该点的投影位置x2必定位于第二幅图像中这条光线投影上的某个位置。三维空间中的光线在二维空间中的投影就是所谓的极线。这种几何关系告诉我们一些重要信息：对于第一幅图像中的任意点，其在第二幅图像中的对应点被限制在一条线上。这就是所谓的极线约束。

1.2 极点

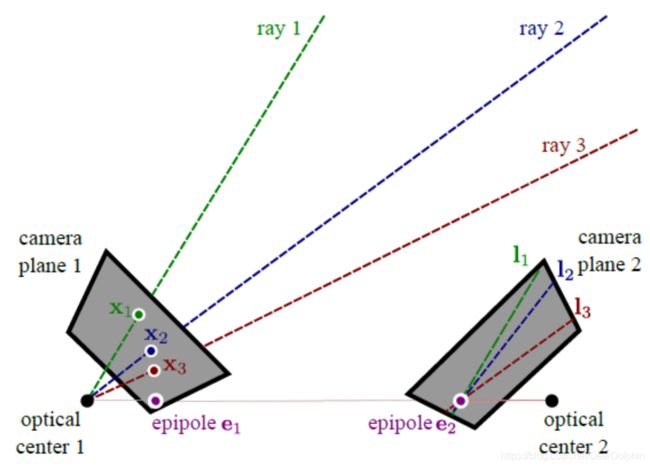
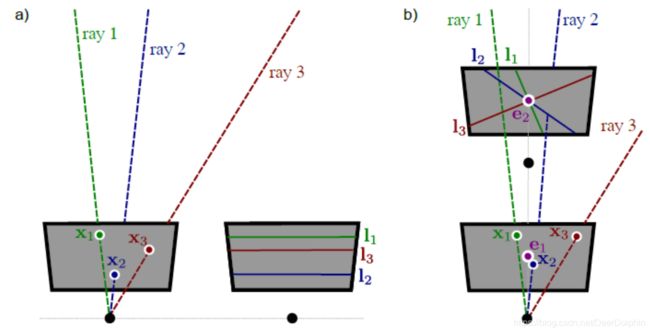
　　图像中每一个点都与三维空间中的一条光线相关联，每一条光线都在第二幅图像中投影而形成极线。由于所有的光线都汇聚于第一个摄像机的光心，所以极线必须汇聚于第二幅图像平面上的一个点。这是第一个摄像机的光心在第二个摄像机中的图像，称为极点。
　　极点并不一定位于观测图像内：极线也可能汇聚于可视范围之外的某一点。当两个摄像机都位于同一方向（即没有相对旋转）且垂直于光轴时，极线是相互平行的，因此由极线汇聚的极点就位于无穷远处。当两个摄像机位于同一方向且平行于光轴时，极点就位于图像的中心且极线呈放射状。

1.3 基本矩阵F（8点算法）

一对对应点$$m_i=[u_i,v_i,1{]}^T,m_i^{\prime }=[u_i^{\prime },v_i^{\prime },1{]}^T$$之间满足约束：$$m_i^{\prime T}{F}^{\prime }{m}_i=0$$
$$F=\left[\begin{array}{ccc}{F}_{11}& F_{12}& F_{13}\\ F_{21}& F_{22}& F_{23}\\ F_{31}& F_{32}& F_{33}\end{array}\right]$$
展开可以得到约束方程为:
$$u_i^{\prime }{u}_i^{\prime }{F}_{11}+u_i^{\prime }{v}_i^{\prime }{F}_{12}+u_i^{\prime }{F}_{13}+v_i^{\prime }{u}_i{F}_{21}+v_i^{\prime }{v}_i{F}_{22}+v_i^{\prime }{F}_{23}+u_i{F}_{31}+v_i{F}_{32}+F_{33}=0$$
对于n对对应的图像点对mi<->mi_'i=1…n可得到n个这样的方程
构造向量：
$$f=[F_{11},F_{12},F_{13},F_{21},F_{22},F_{23},F_{31},F_{32},F_{33}{]}^T$$
构造矩阵：

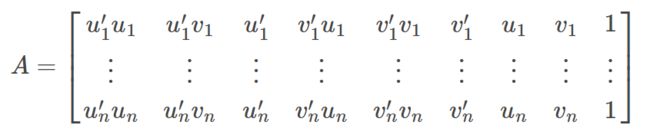
从而：$$Af=0$$当n>=8,可以线性求解f。

基于代数误差的估计方法是满足某些约束下使$$||Af||$$最小的算法

• 由对应点（n>=8）集构造矩阵A；

• 对A进行奇异值分解$$A=UD{V}^T$$,由向量$$f=v_9$$构造矩阵F；

• 对F进行SVD分解$$F=Udiag(s1s_2{s}_3)V^T$$得到基本矩阵的估计F^$$=Udiag(s_1{s}_{2}0)V^T$$

• 8点算法估计基本矩阵F的结果与图像点的坐标系有关。当图像数据有噪声，即对应点不精确时，由8点算法给出的基本矩阵F的解精度很低。

• 存在一种归一化坐标系，在此坐标系下估计的基本矩阵优于其它坐标系。

• 归一化变换：

1. 对图像点做位移变换，使得图像的原点位于图像点集的质心；
2. 对图像点做缩放变换，使得图像点分布在以质心为圆心半径为$${\surd }_2$$

• 归一化8点算法：由对应点$$m_i<->m_i^{\prime }$$，求F

1. 对两幅图像分别做归一化变换$$H，H_i^{\prime }，$$得到新的对应点集；
2. 有新的对应点集和8点算法估计F^；
3. 基本矩阵
   

2. 实验过程

2.1 实验要求

1. 分别用七点、八点、十点（匹配点），计算基础矩阵
   实验图片包含三种情况，即
   （1）左右拍摄，极点位于图像平面上
   （2）像平面接近平行，极点位于无穷远
   （3）图像拍摄位置位于前后
2. 针对上述情况，画出极点和极线，其中点坐标要均匀分布于各行
3. 避免只用排在前五特征点的方式

2.3 实验准备

1. 实验数据集
   （1）左右拍摄
   
   （2）相平面接近平行
   
   （3）图像拍摄位置位于前后
   

2.4 实验结果

2.4.1 求基础矩阵F（8点法）

• 左右拍摄
  （1）sift特征匹配
  （2）ransac筛选匹配点
  
  （3）八点法匹配结果
  
  （4）基础矩阵F
  
• 相平面接近平行
  （1）sift特征匹配
  
  （2）ransac筛选匹配点
  
  （3）八点法匹配结果
  
  （4）基础矩阵F
  
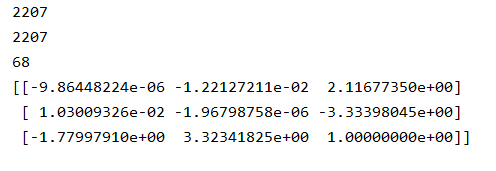
• 图像拍摄位置位于前后
  （1）sift特征匹配
  
  （2）ransac筛选匹配点
  
  （3）八点法匹配结果
  
  （4）基础矩阵F
  

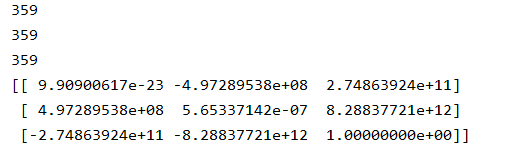
4.4.2 画出极点，极线

（1）左右拍摄

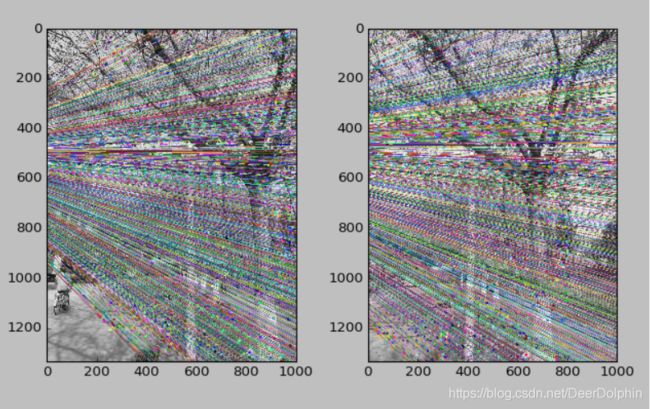
（2）相平面接近平行

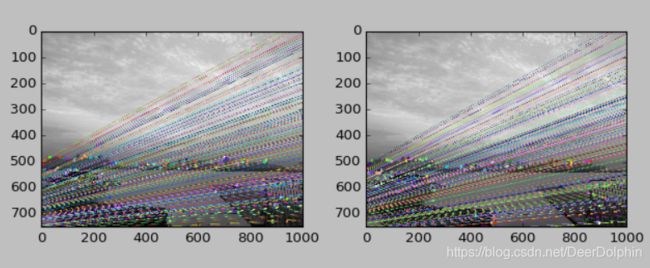
（3）图像拍摄位置位于前后

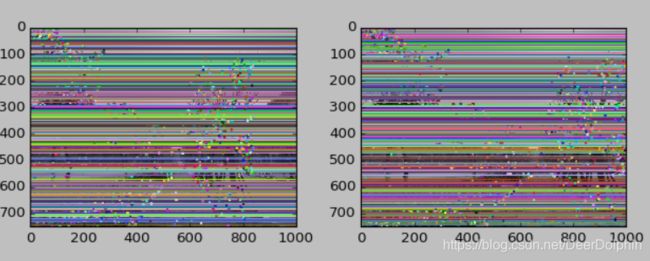
2.5 实验总结

• 从极点，极限的描绘结果来看：

1. 我这组数据集的实验结果是比较失败的，左右拍摄时极点再图像上时比较好的结果，但是忧郁我两张图片左右拍摄的角度，移动不大，导致极点再图像外左侧边的位置，应适当增加左右拍摄的角度，极点才会交在在图像上；
2. 像平面接近平行时：效果还行，但还是没达到理想的极线趋近平行的样子，不是太明白原因，因为两张图片是在同一水平和角度下拍摄的，对极线应该是趋于平行的样子；
3. 拍摄位置位于前后这一组的结果直接变成了像平面平行时的效果，这应该归咎于我的拍摄，这两张图总体区别不大，只有一点点远近位置的差异，所以大体上变符合了平行时的条件，以至于对极线都平行了。
4. 有很多组图片我都跑不出结果，即使图片大小、像素都一样，总会报错，我发现无论是求基本矩阵的代码，还是显示极点极线的代码，对图片规格的要求都比较高，很多图片都不能运行通过。

2.6 遇到的问题

1. 运行时报错：AttributeError: module ‘cv2.cv2’ has no attribute ‘SIFT’
   这是因为：还缺少一个包，cmd打开命令窗口，输入： pip install opencv-contrib-python
   运行报错：Set OPENCV_ENABLE_NONFREE CMake option and rebuild the library in function ‘cv::xfeatures2d::SIFT::create’
   解决：将opencv版本退到3.4.2即可解决，卸载之前的包（pip uninstall opencv-python），然后pip install opencv-python3.4.2.16
   pip install opencv-contrib-python3.4.2.16
   运行又报错：AttributeError: module ‘cv2.cv2’ has no attribute ‘xfeatures2d’
   这是因为：opencv将SIFT等算法整合到xfeatures2d集合里面了。
   siftDetector=cv2.SIFT()变更为siftDetector= cv2.xfeatures2d.SIFT_create()
2. 当图片像素过高或两张图片长宽大小不一致时也会报错，直接将像素值调低，让同一组的两张图片格式大小yi’zhi再尝试运行即可；
3. 运行时报错：（未解决）

参考链接：
[1] https://www.cnblogs.com/majiale/p/9306039.html
[2] https://www.cnblogs.com/jqpy1994/p/10561891.html