计算运动图像序列的运动矢量
计算运动图像序列的运动矢量
- 光流法
- 假设
- 光流方程的求解推导
- 解的唯一性问题
- Lucas-Kanade方法
- 代码
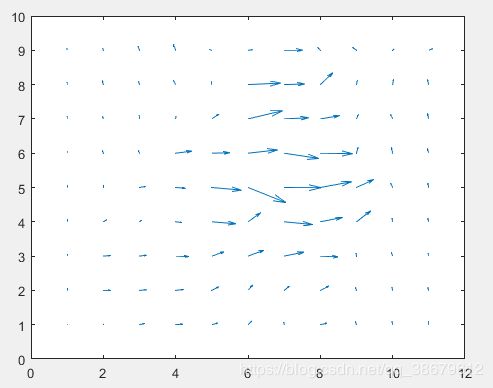
- 结果展示
光流法
假设
二维平面上的亮度变化可以看着是一个连续的流体，因此在物体运动的轨迹上亮度信号的强度基本保持不变。
I ( r ⃗ , t ) = I ( r ⃗ − d ⃗ , t − Δ t ) I(\vec{r},t)=I(\vec{r}-\vec{d},t-\Delta t) I(r,t)=I(r−d,t−Δt)
光流方程的求解推导
泰勒展开：
I ( r ⃗ − d ⃗ , t − Δ t ) = I ( r ⃗ , t ) − d ⃗ ⋅ ∇ ⃗ I ( r ⃗ , t ) − Δ t ∂ I ( r ⃗ , t ) ∂ t I(\vec{r}-\vec{d},t-\Delta t)=I(\vec{r},t)-\vec{d}·\vec{\nabla}I(\vec{r},t)-\Delta t \frac{\partial I(\vec{r},t)}{\partial t} I(r−d,t−Δt)=I(r,t)−d⋅∇I(r,t)−Δt∂t∂I(r,t)
两边除以 Δ t \Delta t Δt：
V ⃗ ⋅ ∇ ⃗ I ( r ⃗ , t ) + ∂ I ( r ⃗ , t ) ∂ t = 0 \vec{V}·\vec{\nabla}I(\vec{r},t)+\frac{\partial I(\vec{r},t)}{\partial t}=0 V⋅∇I(r,t)+∂t∂I(r,t)=0
其中， V ⃗ = ( u , v ) \vec{V}=(u,v) V=(u,v)
解的唯一性问题
1、垂直与梯度方向的运动矢量具有不确定解。
2、当梯度为零时，运动矢量具有不确定解。
Lucas-Kanade方法
对每个运动矢量的求解都取n×n的块区域，例如3×3，我们认为其中所有9点都有相同的运动矢量。所以现在我们的问题变成了求解9个有两个未知变量的方程，这些变量是超定的。使用最小二乘拟合法可以获得更好的解决方案：
[ u v ] = [ ∑ i = 1 9 I x i 2 ∑ i = 1 9 I x i ⋅ I y i ∑ i = 1 9 I x i ⋅ I y i ∑ i = 1 9 I y i 2 ] − 1 ⋅ [ − ∑ i = 1 9 I x i ⋅ I t i − ∑ i = 1 9 I y i ⋅ I t i ] [\begin{matrix} u\\ v\\ \end{matrix}]= [\begin{matrix} \sum_{i=1}^9 I_{x_i}^2 & \sum_{i=1}^9 I_{x_i}·I_{y_i}\\ \sum_{i=1}^9 I_{x_i}·I_{y_i} & \sum_{i=1}^9 I_{y_i}^2\\ \end{matrix}]^{-1}· [\begin{matrix} -\sum_{i=1}^9 I_{x_i}·I_{t_i}\\ -\sum_{i=1}^9 I_{y_i}·I_{t_i}\\ \end{matrix}] [uv]=[∑i=19Ixi2∑i=19Ixi⋅Iyi∑i=19Ixi⋅Iyi∑i=19Iyi2]−1⋅[−∑i=19Ixi⋅Iti−∑i=19Iyi⋅Iti]
代码
pic1 = imread('foreman5.bmp');
pic2 = imread('foreman6.bmp');
pic1_gray = double(rgb2gray(pic1));
pic2_gray = double(rgb2gray(pic2));
%为了计算方便化为灰度图
my_size = 32; %块的大小，可调，例如4、8、16、32等
%这里注意，因为我选用的图片大小为288*352，长宽都可以被4、8、
%16、32整除，故选用这些块大小。若图片不能被整除，则边缘一些
%像素无法被计算运动矢量
[n,m] = size(pic1_gray);
new_n = fix(n/my_size);
new_m = fix(m/my_size); %将图像按照块的大小分配区域
%fix为取整，是为了考虑上面所说无法整除的情况
pic2_ex = [pic2_gray,pic2_gray(:,m);pic2_gray(n,:),0];
%为了计算Ix、Iy在边缘进行周期延拓，原因可参考原理公式
u = zeros(new_n,new_m);
v = zeros(new_n,new_m); %每个区域对应一个(u,v)
for fi=1:new_n
for fj=1:new_m %这两个循环是块的遍历
i = 1 + my_size*(fi-1);
j = 1 + my_size*(fj-1);
%i，j为每个块的最左上角像素位置
A = zeros(2,2); %LK方程等式右边的第一个矩阵
b = zeros(2,1); %LK方程等式右边的第二个矩阵
for i_ = 1:my_size
for j_ = 1:my_size
%这里两个循环是每个块内计算A、b矩阵进而求运动矢量
fx = pic2_ex((i+i_-1)+1,(j+j_-1)) - pic2_ex((i+i_-1),(j+j_-1));
fy = pic2_ex((i+i_-1),(j+j_-1)+1) - pic2_ex((i+i_-1),(j+j_-1));
ft = pic2_ex((i+i_-1),(j+j_-1)) - pic1_gray((i+i_-1),(j+j_-1));
A(1,1) = A(1,1) + fx^2;
A(1,2) = A(1,2) + fx * fy;
A(2,1) = A(1,2);
A(2,2) = A(2,2) + fy^2;
b(1,1) = b(1,1) - fx * ft;
b(2,1) = b(2,1) - fy * ft;
end
end
re = inv(A)*b;
u(fi,fj) = re(1);
v(fi,fj) = re(2);
end
end
quiver(v,u); %显示运动矢量图
结果展示
第一帧：
第二帧：
分析：这两帧的运动主要是男人在向右转头（镜头视角的右），周围区域基本不动。
运动矢量图：
可以看到基本符合。