基于TensorFlow卷积神经网络的手写体数字识别

一、卷积神经网络（CNN）

二、LeNet

三、代码

1、Mnist手写体训练并测试

 2、可视化

四、数据集分析

五、结果分析

1、准确率

2、可视化测试

---

一、卷积神经网络（CNN）

参考：https://blog.csdn.net/yunpiao123456/article/details/52437794

          https://www.cnblogs.com/skyfsm/p/6790245.html

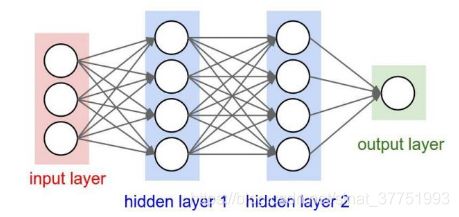
我们知道传统的神经网络是这样的：

      卷积神经网络依旧是层级网络，只是层的功能和形式做了变化，可以说是传统神经网络的一个改进。近年来卷积神经网络在多个方向持续发力，在语音识别、人脸识别、通用物体识别、运动分析、自然语言处理甚至脑电波分析方面均有突破。

     卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出对之间的映射能力。

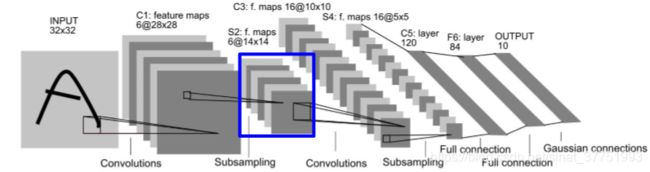
二、LeNet

参考：https://blog.csdn.net/zhangjunhit/article/details/53536915

     LeNet5诞生于1994年，是最早的卷积神经网络之一， 由Yann LeCun完成，推动了深度学习领域的发展。在那时候，没有GPU帮助训练模型，甚至CPU的速度也很慢，因此，LeNet5通过巧妙的设计，利用卷积、参数共享、池化等操作提取特征，避免了大量的计算成本，最后再使用全连接神经网络进行分类识别，这个网络也是最近大量神经网络架构的起点，给这个领域带来了许多灵感。

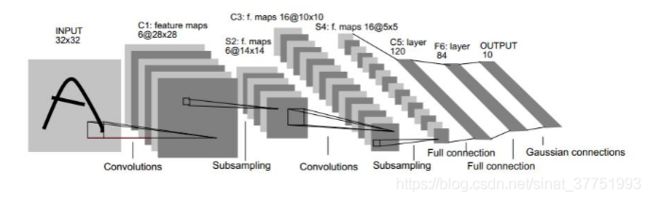
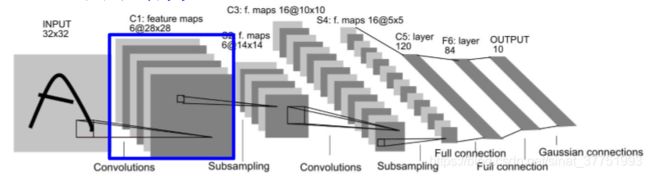
 C1层：卷积层

输入层为32*32图像，卷积核大小为5*5 ，卷积层为6副28*28的特征图

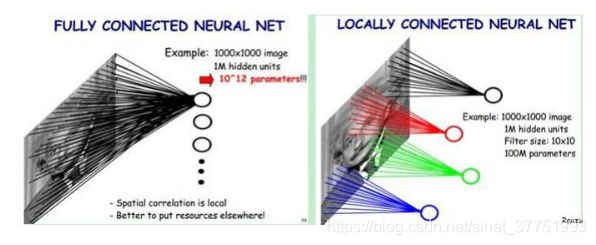
C1层神经元连接数量为28*28*(5*5+1)*6=122304，由于采用了权值共享， 因此待学习参数为(5*5+1)*6=156。如果采用全连接策略，总参数量可达(32*32+1)*(28*28)*6
 

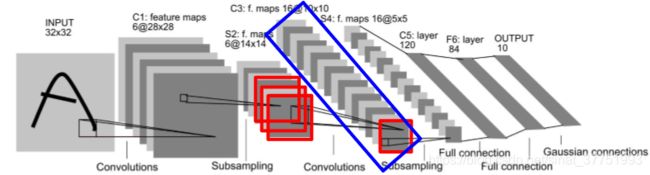
S2层：池化层

Pooling层将28*28的特征图将采样为14*14的图像，采用2*2非重叠采样。 S2层每个单元的4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。 结果通过sigmoid函数计算。S2层神经元连接数量为14*14*(2*2+1)*6=5880，待学习参数为6*2=12。

C3层：卷积层

将6副28*28的特征图卷积为16副10*10的图像，卷积核为5*5： C3 中每副特征图与S2中的若干副特征图相关。C3层神经元连接数量为151600，待学习参数为1516。

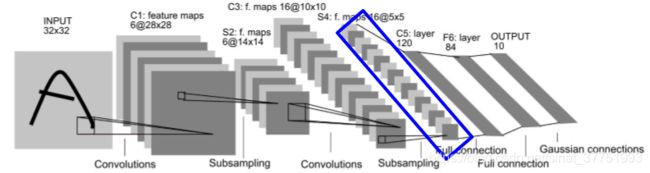
S4层：池化层

将10*10的特征图将采样为16副5*5的图像：降采样过程与S2层一致
S4层神经元连接数量为5*5*(2*2+1)*16=2000，待学习参数为16*2=32

C5层：全连接层

将16副5*5的特征图卷积为长度为120的向量：F6中每个神经元与S4所有神经元相连。C5层神经元连接数量为120*(16*25+1) = 48120，全部为待学习参数。
 

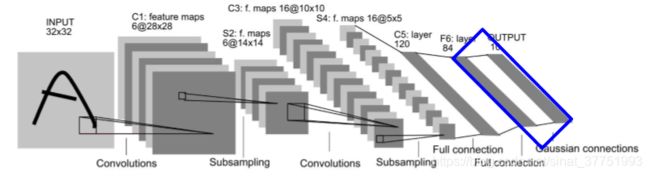
F6层：全连接层

构建84个神经元，每个神经元与C5的120个神经元全连接： F6层神经元连接数量为84*(120+1)=10164，全部为待学习参数。
 

OUTPUT：输出层

为10个神经元，每个神经元的激活值表示对应字符的相应强度， 最大值则为对应的识别结果。
 

三、代码

1、Mnist手写体训练并测试

#coding:utf8
import os 
import cv2 
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

sess = tf.InteractiveSession()


def getTrain():
    train=[[],[]] # 指定训练集的格式，一维为输入数据，一维为其标签
    # 读取所有训练图像，作为训练集
    train_root="mnist_train" 
    labels = os.listdir(train_root)
    for label in labels:
        imgpaths = os.listdir(os.path.join(train_root,label))
        for imgname in imgpaths:
            img = cv2.imread(os.path.join(train_root,label,imgname),0)
            array = np.array(img).flatten() # 将二维图像平铺为一维图像
            array=MaxMinNormalization(array)
            train[0].append(array)
            label_ = [0,0,0,0,0,0,0,0,0,0]
            label_[int(label)] = 1
            train[1].append(label_)
    train = shuff(train)
    return train

def getTest():
    test=[[],[]] # 指定训练集的格式，一维为输入数据，一维为其标签
    # 读取所有训练图像，作为训练集
    test_root="mnist_test" 
    labels = os.listdir(test_root)
    for label in labels:
        imgpaths = os.listdir(os.path.join(test_root,label))
        for imgname in imgpaths:
            img = cv2.imread(os.path.join(test_root,label,imgname),0)
            array = np.array(img).flatten() # 将二维图像平铺为一维图像
            array=MaxMinNormalization(array)
            test[0].append(array)
            label_ = [0,0,0,0,0,0,0,0,0,0]
            label_[int(label)] = 1
            test[1].append(label_)
    test = shuff(test)
    return test[0],test[1]

def shuff(data):
    temp=[]
    for i in range(len(data[0])):
        temp.append([data[0][i],data[1][i]])
    import random
    random.shuffle(temp)
    data=[[],[]]
    for tt in temp:
        data[0].append(tt[0])
        data[1].append(tt[1])
    return data

count = 0
def getBatchNum(batch_size,maxNum):
    global count
    if count ==0:
        count=count+batch_size
        return 0,min(batch_size,maxNum)
    else:
        temp = count
        count=count+batch_size
        if min(count,maxNum)==maxNum:
            count=0
            return getBatchNum(batch_size,maxNum)
        return temp,min(count,maxNum)
    
def MaxMinNormalization(x):
    x = (x - np.min(x)) / (np.max(x) - np.min(x))
    return x


# 1、权重初始化,偏置初始化
# 为了创建这个模型，我们需要创建大量的权重和偏置项
# 为了不在建立模型的时候反复操作，定义两个函数用于初始化
def weight_variable(shape):
    initial = tf.truncated_normal(shape,stddev=0.1)#正太分布的标准差设为0.1
    return tf.Variable(initial)
def bias_variable(shape):
    initial = tf.constant(0.1,shape=shape)
    return tf.Variable(initial)


# 2、卷积层和池化层也是接下来要重复使用的，因此也为它们定义创建函数
# tf.nn.conv2d是Tensorflow中的二维卷积函数，参数x是输入，w是卷积的参数
# strides代表卷积模块移动的步长，都是1代表会不遗漏地划过图片的每一个点，padding代表边界的处理方式
# padding = 'SAME'，表示padding后卷积的图与原图尺寸一致，激活函数relu()
# tf.nn.max_pool是Tensorflow中的最大池化函数，这里使用2 * 2 的最大池化，即将2 * 2 的像素降为1 * 1的像素
# 最大池化会保留原像素块中灰度值最高的那一个像素，即保留最显著的特征，因为希望整体缩小图片尺寸
# ksize：池化窗口的大小，取一个四维向量，一般是[1,height,width,1]
# 因为我们不想再batch和channel上做池化，一般也是[1,stride,stride,1]
def conv2d(x, w):
    return tf.nn.conv2d(x, w, strides=[1,1,1,1],padding='SAME') # 保证输出和输入是同样大小
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1],padding='SAME')
    
iterNum = 1000
batch_size=1024

print("load train dataset.")
train=getTrain()
print("load test dataset.")
test0,test1=getTest()


# 3、参数
# 这里的x,y_并不是特定的值，它们只是一个占位符，可以在TensorFlow运行某一计算时根据该占位符输入具体的值
# 输入图片x是一个2维的浮点数张量，这里分配给它的shape为[None, 784]，784是一张展平的MNIST图片的维度
# None 表示其值的大小不定，在这里作为第1个维度值，用以指代batch的大小，means x 的数量不定
# 输出类别y_也是一个2维张量，其中每一行为一个10维的one_hot向量，用于代表某一MNIST图片的类别
x = tf.placeholder(tf.float32, [None,784], name="x-input")
y_ = tf.placeholder(tf.float32,[None,10]) # 10列


# 4、第一层卷积，它由一个卷积接一个max pooling完成
# 张量形状[5,5,1,32]代表卷积核尺寸为5 * 5，1个颜色通道，32个通道数目
w_conv1 = weight_variable([5,5,1,32])
b_conv1 = bias_variable([32]) # 每个输出通道都有一个对应的偏置量
# 我们把x变成一个4d 向量其第2、第3维对应图片的宽、高，最后一维代表图片的颜色通道数(灰度图的通道数为1，如果是RGB彩色图，则为3)
x_image = tf.reshape(x,[-1,28,28,1])
# 因为只有一个颜色通道，故最终尺寸为[-1，28，28，1]，前面的-1代表样本数量不固定，最后的1代表颜色通道数量
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conv1) # 使用conv2d函数进行卷积操作，非线性处理
h_pool1 = max_pool_2x2(h_conv1)                          # 对卷积的输出结果进行池化操作


# 5、第二个和第一个一样，是为了构建一个更深的网络，把几个类似的堆叠起来
# 第二层中，每个5 * 5 的卷积核会得到64个特征
w_conv2 = weight_variable([5,5,32,64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2)# 输入的是第一层池化的结果
h_pool2 = max_pool_2x2(h_conv2)

# 6、密集连接层
# 图片尺寸减小到7 * 7，加入一个有1024个神经元的全连接层，
# 把池化层输出的张量reshape(此函数可以重新调整矩阵的行、列、维数)成一些向量，加上偏置，然后对其使用Relu激活函数
w_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1,7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1) + b_fc1)

# 7、使用dropout，防止过度拟合
# dropout是在神经网络里面使用的方法，以此来防止过拟合
# 用一个placeholder来代表一个神经元的输出
# tf.nn.dropout操作除了可以屏蔽神经元的输出外，
# 还会自动处理神经元输出值的scale，所以用dropout的时候可以不用考虑scale
keep_prob = tf.placeholder(tf.float32, name="keep_prob")# placeholder是占位符
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)


# 8、输出层，最后添加一个softmax层
w_fc2 = weight_variable([1024,10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, w_fc2) + b_fc2, name="y-pred")


# 9、训练和评估模型
# 损失函数是目标类别和预测类别之间的交叉熵
# 参数keep_prob控制dropout比例，然后每100次迭代输出一次日志
cross_entropy = tf.reduce_sum(-tf.reduce_sum(y_ * tf.log(y_conv),reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
# 预测结果与真实值的一致性，这里产生的是一个bool型的向量
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
# 将bool型转换成float型，然后求平均值，即正确的比例
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 初始化所有变量，在2017年3月2号以后,用 tf.global_variables_initializer()替代tf.initialize_all_variables()
sess.run(tf.initialize_all_variables())

# 保存最后一个模型
saver = tf.train.Saver(max_to_keep=1)


for i in range(iterNum):
    for j in range(int(len(train[1])/batch_size)):
        imagesNum=getBatchNum(batch_size,len(train[1]))
        batch = [train[0][imagesNum[0]:imagesNum[1]],train[1][imagesNum[0]:imagesNum[1]]]
        train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
    if i % 2 == 0:
        train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1],keep_prob: 1.0})
        print("Step %d ,training accuracy %g" % (i, train_accuracy))
print("test accuracy %f " % accuracy.eval(feed_dict={x: test0, y_:test1, keep_prob: 1.0})) 
# 保存模型于文件夹
saver.save(sess,"save/model")

 2、可视化

import tensorflow as tf
import numpy as np
import tkinter as tk
from tkinter import filedialog
from PIL import Image, ImageTk
from tkinter import filedialog
import time


def creat_windows():
    win = tk.Tk() # 创建窗口
    sw = win.winfo_screenwidth()
    sh = win.winfo_screenheight()
    ww, wh = 400, 450
    x, y = (sw-ww)/2, (sh-wh)/2
    win.geometry("%dx%d+%d+%d"%(ww, wh, x, y-40)) # 居中放置窗口

    win.title('手写体识别') # 窗口命名

    bg1_open = Image.open("timg.jpg").resize((300, 300))
    bg1 = ImageTk.PhotoImage(bg1_open)
    canvas = tk.Label(win, image=bg1)
    canvas.pack()


    var = tk.StringVar() # 创建变量文字
    var.set('')
    tk.Label(win, textvariable=var, bg='#C1FFC1', font=('宋体', 21), width=20, height=2).pack()

    tk.Button(win, text='选择图片', width=20, height=2, bg='#FF8C00', command=lambda:main(var, canvas), font=('圆体', 10)).pack()
    
    win.mainloop()

def main(var, canvas):
    file_path = filedialog.askopenfilename()
    bg1_open = Image.open(file_path).resize((28, 28))
    pic = np.array(bg1_open).reshape(784,)
    bg1_resize = bg1_open.resize((300, 300))
    bg1 = ImageTk.PhotoImage(bg1_resize)
    canvas.configure(image=bg1)
    canvas.image = bg1

    init = tf.global_variables_initializer()

    with tf.Session() as sess:
            sess.run(init)
            saver = tf.train.import_meta_graph('save/model.meta')  # 载入模型结构
            saver.restore(sess, 'save/model')  # 载入模型参数
            graph = tf.get_default_graph()       # 加载计算图
            x = graph.get_tensor_by_name("x-input:0")  # 从模型中读取占位符变量
            keep_prob = graph.get_tensor_by_name("keep_prob:0")
            y_conv = graph.get_tensor_by_name("y-pred:0")  # 关键的一句  从模型中读取占位符变量
            prediction = tf.argmax(y_conv, 1)
            predint = prediction.eval(feed_dict={x: [pic], keep_prob: 1.0}, session=sess)  # feed_dict输入数据给placeholder占位符
            answer = str(predint[0])
    var.set("预测的结果是：" + answer)

if __name__ == "__main__":
    creat_windows()

四、数据集分析

本次采用的是Mnist手写数字集，每张图片的大小都是28*28的灰度图，根据数字的类别进行分类存放，如下图所示

      

通过观察数据集中的数字可以发现，在同一数字的情况下，不同的书写风格，字的粗细大小，所呈现出的形态是完全不同的，有时即使是肉眼都无法准确识别该数字，例如：

  （数字9，由于上半部分的圈过大，看起来有点像数字0）

    （数字7，由于下面多了小勾勾，看起来像数字2）

字体奇异的，扭曲的

             

字体过粗，导致看不清的

   

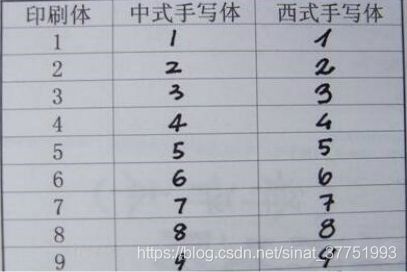
存在西式手写体

    

 

五、结果分析

1、准确率

       通过运行结果可以看出，每隔两次迭代一次，准确率与迭代次数成正比关系，随着迭代次数的增加，准确率将趋于100%。并且，第0次迭代时，准确率是83.98%，经过第8次迭代，准确率就达到了98.34%。由此可以看出迭代前期的准确率提升很快。在后期，随着迭代次数的增加，准确率的提升速度将会减慢，并无限趋于100%。

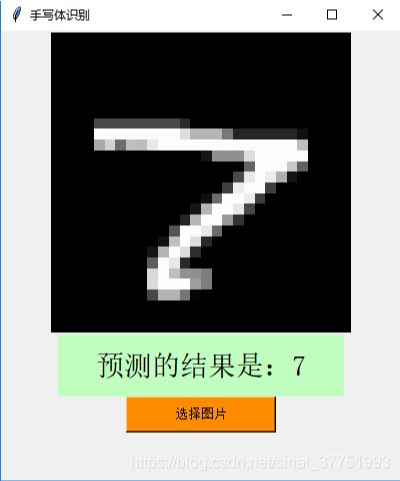
2、可视化测试

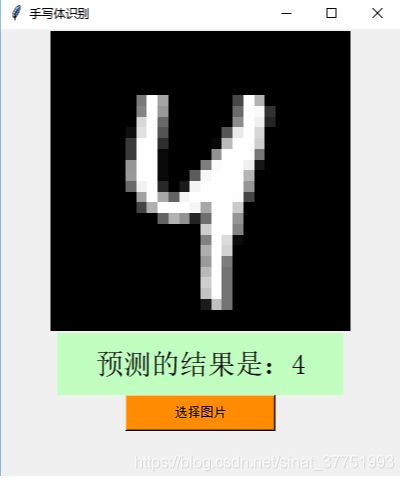
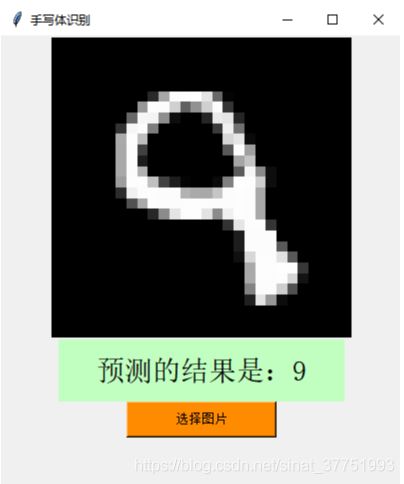
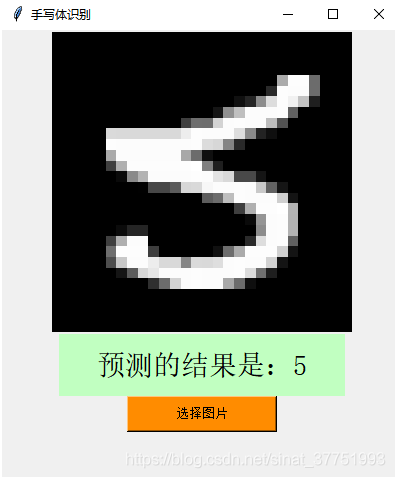
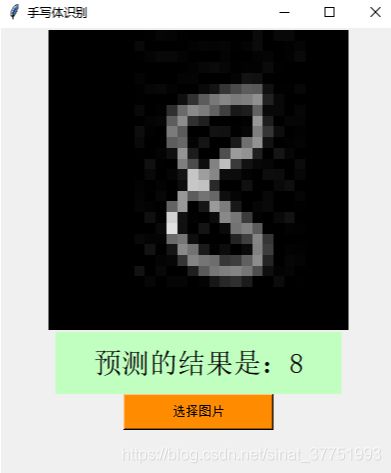
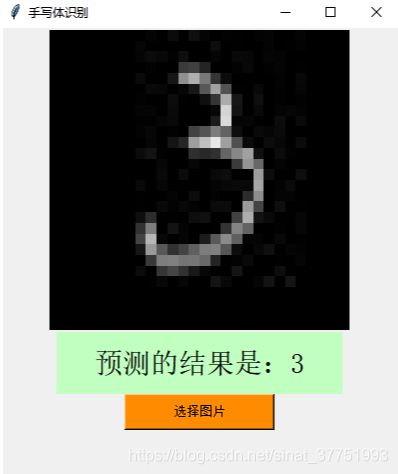
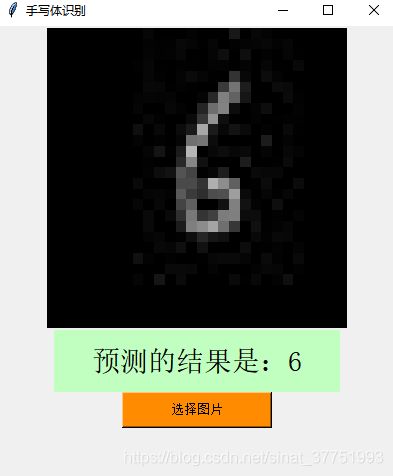
用Mnist训练集可视化的结果：

      

由于该训练集之大，训练的准确率之高，即使是形态各异的奇葩数字都可以准确的识别出来。

为此，我自己手写了一些数据集来进行测试

别忘记了将这些图像，转换成大小为28*28的灰度图

这里提供下，用python批量转换成灰度图的代码，供大家参考

from PIL import Image
import os
 
input_dir = 'F:/计算机视觉/实验十/Mnist手写体训练/Mnist手写体训练/test/test2/'
out_dir = 'F:/计算机视觉/实验十/Mnist手写体训练/Mnist手写体训练/test/gray2/'
a = os.listdir(input_dir)
 
for i in a:
    print(i)
    I = Image.open(input_dir+i)
    L = I.convert('L')
    L.save(out_dir+i)

识别正确的：

      

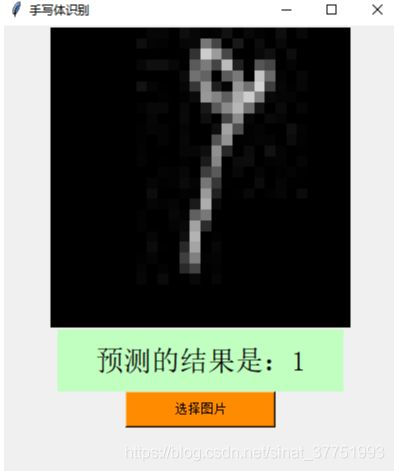
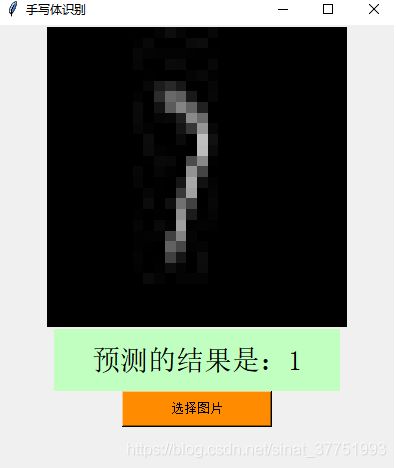
识别错误的：

   

9识别成1，主要是因为9上面的圈太小了，在识别时，一下子就识别到下面的竖，而忽视上面的小圆圈，从而导致识别成了1。

同理，7识别成1也是这样。

     并且，原先的Mnist训练集集中存在很多像这样的西式手写体，而我们的书写习惯也是中式的手写体，这可能也是识别失败的原因之一。