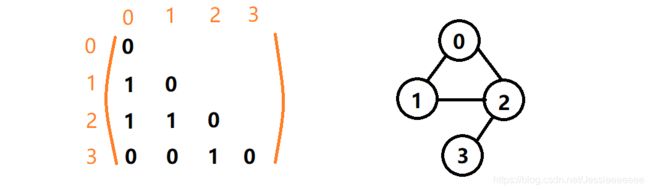数据结构 第六章 图 作业（已批改）

判断题

1-1
无向连通图至少有一个顶点的度为1。

T F

可参考课本P150的定义：在无向图G中，如果对于图中任意两个顶点都是连通的（有路径），则称G是连通图；

1-2
用一维数组G[]存储有4个顶点的无向图如下：G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }，则顶点2和顶点0之间是有边的。

T F

无向图的邻接矩阵沿主对角线对称；

1-3
若图G有环，则G不存在拓扑排序序列。

T F

拓扑排序不设考点，跳过；

1-4
无向连通图所有顶点的度之和为偶数。

T F

1-5
无向连通图边数一定大于顶点个数减1。

T F

如果定点数为3，则边数为2，边数=定点个数减1；

1-6
用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。

T F

课本P156：邻接表由两部分组成：表头结点表和边表；
所以用邻接表法存储图，占用的存储空间数只与图中结点个数和边数都有关；

1-7
用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。

T F

课本P154：用邻接矩阵表示法表示图，除了一个用于存储邻接矩阵的二维数组外，还需要一个一维数组来存储顶点信息；

1-8
在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍。

T F

1-9
在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。

T F

1-10
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G一定有2个连通分量。

T F

课本P163：广度优先搜索遍历类似于树的按层次遍历的过程；

1-11
在一个有权无向图中，若b到a的最短路径距离是12，且c到b之间存在一条权为2的边，则c到a的最短路径距离一定不小于10。

T F

1-12
Prim 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。

T F

1-13
Kruskal 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。

T F

克鲁斯卡尔算法是维护一个森林，每一步把两棵树合并成一棵；

1-14
对于带权无向图 G = (V, E)，M 是 G 的最小生成树，则 M 中任意两点 V1 到 V2 的路径一定是它们之间的最短路径。

T F

最小生成树的总权最小，不是其中的任意路径最小；

1-15
如果 e 是有权无向图 G 唯一的一条最短边，那么边 e 一定会在该图的最小生成树上。

T F

单选题

2-1
具有5个顶点的有向完全图有多少条弧？
A. 10
B. 16
C. 20
D. 25

因为在有向完全图中，任何两个顶点之间都有2条弧所以在n个顶点中选取两个顶点的选法有n(n-1)/2所以共有2*n(n-1)/2=n(n-1)条弧。
因而 5 × 4 = 20
课本P150：对于有向图，若具有 n(n-1) 条弧，则称为有向完全图；

2-2
对于一个具有N个顶点的无向图，要连通所有顶点至少需要多少条边？
A. N−1
B. N
C. N+1
D. N/2

连通是两个顶点之间有路径即连通，N-1条就够了。

2-3
若一个有向图用邻接矩阵表示，则第 i 个结点的入度就是：
A. 第i行的元素个数
B. 第i行的非零元素个数
C. 第i列的非零元素个数
D. 第i列的零元素个数

若一个有向图用邻接矩阵表示，则第i个结点的入度就是：第i列的非零元素个数；
若一个有向图用邻接矩阵表示，则第i个结点的出度就是：第i行的非零元素个数；

2-4
下面关于图的存储的叙述中，哪一个是正确的？
A. 用相邻矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
B. 用相邻矩阵法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关
C. 用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
D. 用邻接表法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关

用相邻矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关；
用邻接表法存储图，占用的存储空间数只与图中边数和结点个数都有关；

2-5
关于图的邻接矩阵，下列哪个结论是正确的？
A. 有向图的邻接矩阵总是不对称的
B. 有向图的邻接矩阵可以是对称的，也可以是不对称的
C. 无向图的邻接矩阵总是不对称的
D. 无向图的邻接矩阵可以是不对称的，也可以是对称的

有向图的邻接矩阵可以是对称的，也可以是不对称的；
无向图的邻接矩阵总是对称的；

2-6
在一个无向图中，所有顶点的度数之和等于所有边数的多少倍？
A. 1/2
B. 1
C. 2
D. 4

在一个无向图中，所有顶点的度数之和等于所有边数的 2 倍；

2-7
在任一有向图中，所有顶点的入度之和与所有顶点的出度之和的关系是：
A. 相等
B. 大于等于
C. 小于等于
D. 不确定

在一个有向图中，所有顶点的入度之和等于所有顶点出度之和的 1 倍；
课本P150；

2-8
图的深度优先遍历类似于二叉树的：
A. 先序遍历
B. 中序遍历
C. 后序遍历
D. 层次遍历

深度优先搜索DFS（Depth First Search）：访问方式类似于树的前序访问；
广度优先搜索BFS（Breadth First Search）：访问方式类似于树的从树根出发的按层次遍历。

2-9
给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为：

A. V1,V2,V3,V5,V4
B. V1,V3,V4,V5,V2
C. V1,V4,V3,V5,V2
D. V1,V2,V4,V5,V3

过程：
从V1开始，V1指向地址2，地址2对应的结点为V3；
V3指向地址3，地址3对应的结点为V4；
V4无指向，往回走，V3第二个指向地址4，地址4对应的结点为V5；
V5指向地址1，地址1对应的结点为V2；
V2无指向，往回走，V5第二个指向地址3，地址3走过了，V5无指向，往回走，V3无指向，往回走，V1第二个指向地址1，地址1走过了，V1第三个指向地址3，地址3走过了；
都走过了，结束；
V1 -> V3 -> V4 -> V5 -> V2；

2-10
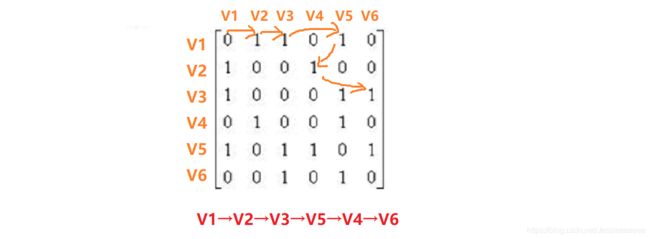
已知一个图的邻接矩阵如下，则从顶点V1出发按深度优先搜索法进行遍历，可能得到的一种顶点序列为：

A. V1,V2,V3,V4,V5,V6
B. V1,V2,V4,V5,V6,V3
C. V1,V3,V5,V2,V4,V6
D. V1,V3,V5,V6,V4,V2

因为此图邻接矩阵沿主对角线对称，所以可能是无向图；

2-11
如果从无向图的任一顶点出发进行一次深度优先搜索可访问所有顶点，则该图一定是：
A. 连通图
B. 完全图
C. 有回路的图
D. 一棵树

深度优先搜索 ≈ 先序遍历；

2-12
给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历，则得到的一种顶点序列为：

A. V1,V2,V3,V4,V5
B. V1,V2,V3,V5,V4
C. V1,V3,V2,V4,V5
D. V1,V4,V3,V5,V2

广度优先搜索法 ≈ 层序遍历；
过程：
从V1出发，第一次指向地址2，地址2为结点V3，第二次指向地址1，地址1为结点V2，第三次指向地址3，地址3为结点V4；
轮到第二个结点V3，第一次指向地址3，地址3走过了跳过，第二次指向地址4，地址4为结点V5；
V1 → V3 → V2 → V4 → V5

2-13
已知一个图的邻接矩阵如下，则从顶点V1出发按广度优先搜索法进行遍历，可能得到的一种顶点序列为：

A. V1,V2,V3,V5,V4,V6
B. V1,V2,V4,V5,V6,V3
C. V1,V3,V5,V2,V4,V6
D. V1,V3,V5,V6,V4,V2

2-14
我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题？
A. Dijkstra算法
B. Kruskal算法
C. 深度优先搜索
D. 拓扑排序算法

2-15
数据结构中Dijkstra算法用来解决哪个问题？
A. 关键路径
B. 最短路径
C. 拓扑排序
D. 字符串匹配

2-16
任何一个带权无向连通图的最小生成树——
A. 是唯一的
B. 是不唯一的
C. 有可能不唯一
D. 有可能不存在

2-17
给定有权无向图的邻接矩阵如下，其最小生成树的总权重是：

A. 10
B. 11
C. 12
D. 14

2-18
下图为一个AOV网，其可能的拓扑有序序列为：

A. ACBDEF
B. ABCEFD
C. ABCDFE
D. ABCEDF

拓扑排序不设考点，跳过；

2-19
在AOE网中，什么是关键路径？
A. 最短回路
B. 最长回路
C. 从第一个事件到最后一个事件的最短路径
D. 从第一个事件到最后一个事件的最长路径

关键路径不设考点，跳过；

2-20
下面给出的有向图中，各个顶点的入度和出度分别是：

A. 入度: 0, 2, 3, 1, 2; 出度: 3, 2, 1, 1, 1
B. 入度: 3, 2, 1, 1, 1; 出度: 0, 2, 3, 1, 2
C. 入度: 3, 4, 4, 2, 3; 出度: 3, 4, 4, 2, 3
D. 入度: 0, 1, 2, 1, 1; 出度: 3, 2, 1, 1, 1

2-21
给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为：

A. V1,V5,V4,V7,V6,V2,V3
B. V1,V2,V3,V4,V7,V6,V5
C. V1,V5,V4,V7,V6,V3,V2
D. V1,V5,V6,V4,V7,V2,V3

深度优先算法 ≈ 先序遍历；
过程：V1→V5→V4→V7→V6→V3→V2

2-22
图的广度优先遍历类似于二叉树的：
A. 先序遍历
B. 中序遍历
C. 层次遍历
D. 后序遍历

2-23
给定一个有向图的邻接表如下图，则该图有__个强连通分量。

A. 4 {{0, 1, 5}, {2}, {3}, {4}}
B. 3 {{2}, {4}, {0, 1, 3, 5}}
C. 1 {0, 1, 2, 3, 4, 5}
D. 1 {0, 5, 1, 3}

2-24
下列选项中，不是下图深度优先搜索序列的是：

A. V​1 , V​5​​ , V​4​​ , V​3​​ , V​2
B. ​​V​1​​ , V​3​​ , V​2​​ , V​5​​ , V​4
​​C. V​1​​ , V​2​​ , V​5​​ , V​4​​ , V​3
​D. V​1​​ , V​2​​ , V​3​​ , V​4​​ , V​5

迷茫？？

​​
2-25
使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：

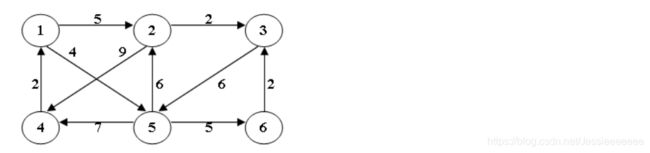
A. 5, 2, 3, 4, 6
B. 5, 2, 3, 6, 4
C. 5, 2, 4, 3, 6
D. 5, 2, 6, 3, 4

2-26
给定有向图的邻接矩阵如下：

顶点2（编号从0开始）的出度和入度分别是：
A. 3, 1
B. 1, 3
C. 0, 2
D. 2, 0

出度为第三行非零元素之和；
入度为第三列非零元素之和；

2-27
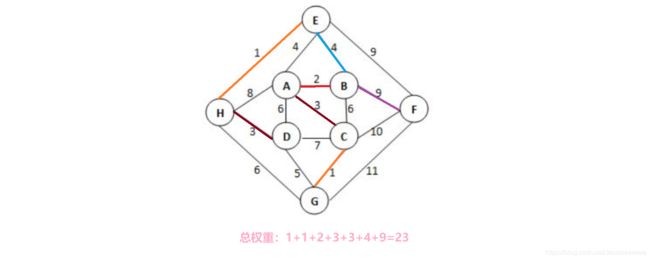
给定有权无向图如下。关于其最小生成树，下列哪句是对的？

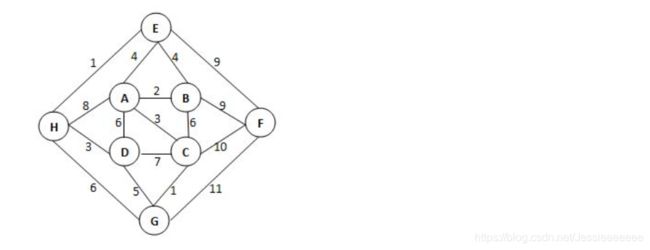
A. 最小生成树不唯一，其总权重为23
B. 最小生成树唯一，其总权重为20
C. 边(B, F)一定在树中，树的总权重为23
D. 边(H, G)一定在树中，树的总权重为20

2-28
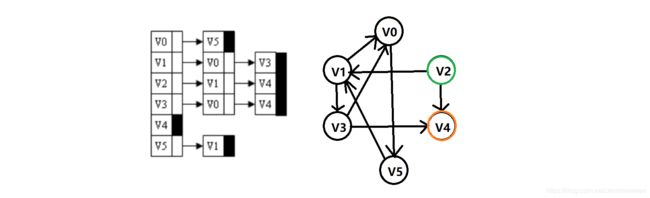
若某图的深度优先搜索序列是{V1, V4, V0, V3, V2}，则下列哪个图不可能对应该序列？

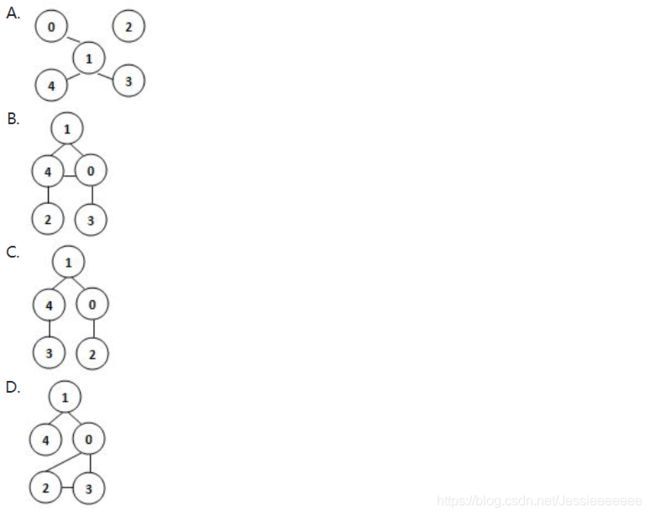
C

深度优先搜索法 ≈ 先序遍历；
C是广度优先算法；

2-29
以下哪个不是给定无向带权图的最小生成树？


D

A：26
B：26
C：26
D：27

2-30
给出如下图所示的具有 7 个结点的网 G，采用Prim算法，从4号结点开始，给出该网的最小生成树。下列哪个选项给出了正确的树结点收集顺序？

A. 4501362
B. 4526301
C. 4561023
D. 4563201

2-31
下面给出的有向图中，有__个强连通分量。

A. 1 ({0,1,2,3,4})
B. 1 ({1,2,3,4})
C. 2 ({1,2,3,4}, {0})
D. 5 ({0}, {1}, {2}, {3}, {4})

2-32
图的广度优先遍历类似于二叉树的：
A. 先序遍历
B. 中序遍历
C. 后序遍历
D. 层次遍历

编程题

7-2 排座位 (25分)

布置宴席最微妙的事情，就是给前来参宴的各位宾客安排座位。无论如何，总不能把两个死对头排到同一张宴会桌旁！这个艰巨任务现在就交给你，对任何一对客人，请编写程序告诉主人他们是否能被安排同席。

输入格式：
输入第一行给出3个正整数：N（≤100），即前来参宴的宾客总人数，则这些人从1到N编号；M为已知两两宾客之间的关系数；K为查询的条数。随后M行，每行给出一对宾客之间的关系，格式为：宾客1 宾客2 关系，其中关系为1表示是朋友，-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行，每行给出一对需要查询的宾客编号。

这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友，朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。

输出格式：
对每个查询输出一行结果：如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；如果他们之间并不是朋友，但也不敌对，则输出OK；如果他们之间有敌对，然而也有共同的朋友，则输出OK but…；如果他们之间只有敌对关系，则输出No way。

输入样例：

7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2

输出样例：

No problem
OK
OK but...
No way

#include 
#include 
#include
#include
#include
using namespace std;

int a[200]={0};
int fz[200][200]={0};
int find(int x){
	int r=x;
	while(1){
		if(a[r]==0){
			return r;
		}
		r=a[r];
	}
//	return r;
}

void add(int n,int m){
	int x=find(n);
	int y=find(m);
	if(x!=y)
	  a[x]=y;
} 

int main(){
	int n,m,k;	//n（≤100）,即前来参宴的宾客总人数		m为已知两两宾客之间的关系数		k为查询的条数
	cin>>n>>m>>k;
	for(int i=0;i<m;i++){
		int q,w,e;
		cin>>q>>w>>e;
		if(e==1){
			add(q,w);	//如果是朋友就添加到一个集合里 
		}
		else{
			fz[q][w]=1;
			fz[w][q]=1;
		}
	}
	for(int i=0;i<k;i++){
		int q,w;
		cin>>q>>w;
		if(find(q)==find(w)&&fz[q][w]!=1){
			printf("No problem\n");
		}
		else if(find(q)==find(w)&&fz[q][w]==1){
			printf("OK but...\n");
		}
		else if(find(q)!=find(w)&&fz[q][w]==0){
			printf("OK\n");
		}
		else if(fz[q][w]==1&&find(q)!=find(w)){
			printf("No way\n");
		}
	}
	return 0;
}