【计算机图形学】基于GPU预计算的大气层光效渲染
基于GPU预计算的大气层光效渲染
前言
本文叙述基于物理模型的大气层光效渲染,不仅考虑单重散射,而且也尝试实现多重散射的效果。主要参考论文为Eric Bruneton和Fabrice Neyret的《Precomputed Atmospheric Scattering》。博文如果错误,欢迎指出,非常感谢。此外,本文较多物理理论和数学推导,代码也比较多。
代码已放至本人的github上:https://github.com/ZeusYang/Atmosphere
大气物理模型
1、大气散射现象
大气散射是指,太阳光在射入大气层时,与大气中的空气分子或空气溶胶等发生相互作用,使得入射的光能以一定的规律在各个方向上进行重新分布的现象。太阳光在射入大气层时,遇到大气分子、尘埃、雨滴等颗粒后,都会发生散射现象。其中一部分的光能会被这些粒子吸收转化为热能,而另一部分光能则会以该粒子为中心,向四面八方扩散开来。所以,在经过了大气的散射作用之后,有部分太阳光将无法抵达地球表面。大气散射在自然界中是一种十分重要而又普遍存在的物理现象,人们平时用肉眼观察到的光很大一部分都是散射光。如果没有大气散射,那么只要不是太阳光直接照射到的位置,都将是完全黑暗的。
2、空气物理模型
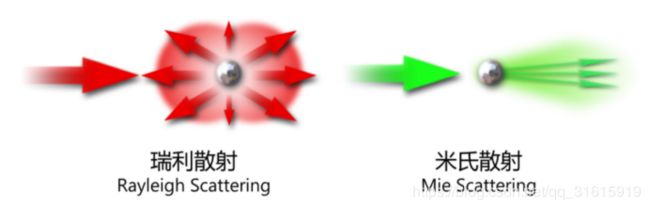
空气中的介质颗粒根据其直径大小的不同可分为两种:直径远小于光线波长的空气微粒、与直径与光线波长相当的空气溶胶。由前者引起的散射我们称为Rayleigh散射,它是导致晴朗天空呈现蓝色的主要原因。由后者引起的散射我们称为Mie散射,它是导致阴霾的天空呈现灰色的原因,因为阴天的空气中存在大量与光波直径相当的水滴。
①Rayleigh散射:由空气中远小于波长的微粒(如空气分子)引起的散射称作瑞利散射。Rayleigh散射强度与光线波长的四次方成反比,这意味着白光中波长较短的颜色光(蓝色)会比波长较长的光(红色)有更强的散射强度,导致天空在白天偏向蓝色,而在黄昏偏向橙红色。 当日出或日落的时候,由于太阳的位置接近地平线,阳光斜射入大气,会在大气层中穿过很长的距离。在这个过程中,太阳光中的蓝色光几乎都会被散射殆尽无法抵达人眼,只剩下了波长较长的红色光,所以在太阳及其周围的天空都会呈现橘红色。
Rayleigh散射的散射系数可以使用如下公式计算:
β R ( θ ) = 2 π 2 ( n 2 − 1 ) 2 3 N λ 4 p R ( θ ) \beta_R(\theta)=\frac{2\pi^2(n^2-1)^2}{3N\lambda^4}p_R(\theta) βR(θ)=3Nλ42π2(n2−1)2pR(θ) (1)
其中 θ \theta θ是视线与太阳光线的夹角, N N N是大气分子密度, n n n是大气的折射率, λ \lambda λ是入射光的波长, p R ( θ ) p_R(\theta) pR(θ)是单位化的相位函数。由上可知,Rayleigh散射明显与波长的四次方成反比,在实现中我们可用一个RGB向量来表示,散射系数可表示为:
β R . r g b = ( 5.81 , 13.5 , 33.1 ) × 1 0 − 6 \beta_R.rgb=(5.81,13.5,33.1)\times10^{-6} βR.rgb=(5.81,13.5,33.1)×10−6 (2)
由于Rayleigh散射几乎是各向同性的,即光线会被粒子向各个方向均匀散射,其相位函数可以表示为:
p R ( θ ) = 3 16 π ( 1 + c o s 2 θ ) ) p_R(\theta)=\frac{3}{16\pi}(1+cos^2\theta)) pR(θ)=16π3(1+cos2θ)) (3)
相位函数描述了散射的方向特征,也就是在视线与光线夹角为 θ \theta θ的情况,在总共散射的光线中有多少被散射到视线方向上,可以理解为概率或者比例。
② Mie散射:在空气中直径与波长相当的微粒(如尘埃、雾滴等)所导致的散射现象称作Mie散射。与Rayleigh散射不同,Mie散射与波长无关,散射方向表现出明显的各向异性,光线会被粒子更多的向后方散射。而当阴雨天气时,空气中存在大量的水滴颗粒,Mie散射导致天空呈现灰白色。现今经常出现的雾霆天气,同样是因为空气中悬浮的大颗粒过多而导致的Mie散射现象。
由于Mie散射与波长无关,故可以用标量表示,Mie散射系数为:
β M . r g b = 2.0 × 1 0 − 5 \beta_M.rgb=2.0\times10^{-5} βM.rgb=2.0×10−5 (4)
Mie散射的方向是各向异性的,光线会被更多的向后方散射,其相位函数为:
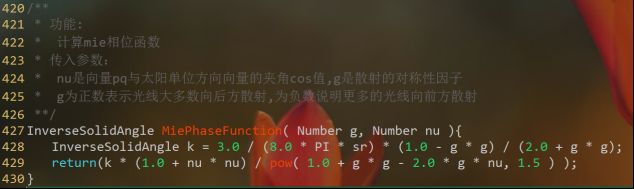
p M ( θ ) = 1 4 π 3 ( 1 − g 2 ) 2 ( 2 + g 2 ) 1 + c o s 2 θ ( 1 + g 2 − 2 g c o s θ ) 3 2 p_M(\theta)=\frac{1}{4\pi}\frac{3(1-g^2)}{2(2+g^2)}\frac{1+cos^2\theta}{(1+g^2-2gcos\theta)^{\frac{3}{2}}} pM(θ)=4π12(2+g2)3(1−g2)(1+g2−2gcosθ)231+cos2θ (5)
在公式(5)中, θ \theta θ是光线方向与视线方向的夹角,而 g g g表示散射的对称性。若 g g g是正值,则大多数光线会被粒子向后方散射;若 g g g是负值,则更多的光线会被向前方散射。通常,g取值[-0.75,0.99]。
③ 大气密度:对于瑞利散射和米氏散射,它们对太阳光的散射作用都和空气粒子的密度有关。许多大气模型都假设摄像机总是在地面上或者是在十分接近地面的位置,这样就可以认为空气具有一个恒定的粒子密度,这就在很大程度上简化了Nishita在1993年提出的散射积分方程,并在近地空间可以得到很好的渲染效果。然而在远离地表的高空,这种做法得到的渲染结果并不准确。
实际中的大气密度在地球引力的作用下,越靠近地表空气密度越高,越远离地表空气越稀薄。所以,我们假定空气粒子的密度是沿着海拔高度h呈指数递减的:
ρ = ρ 0 e − h H \rho=\rho_0e^{-\frac{h}{H}} ρ=ρ0e−Hh 其中 ρ 0 \rho_0 ρ0是在海平面的空气密度 (6)
h h h为当前采样点的海拔高度, H H H是缩放高度(在实现中可设为大气层高度)。理论上说大气层并没有确定的高度,但在实现中我们需要一个统一高度来渲染天空弯顶,这样空气密度随着高度的增加而呈指数递减。对于Rayleigh散射与Mie散射我们分别使用不同的缩放高度: H R = 7994 k m H_R=7994km HR=7994km, H M = 1200 k m H_M=1200km HM=1200km。这是因为影响Mie散射的大颗粒(尘埃、水滴等)更多的存在于近地表的对流层中,再往上Mie散射效果不明显,但Rayleigh散射的作用依然存在。
3、光线内散射
太阳光在大气中传输的时候会与空气中的微粒产生交互作用。有两种重要的交互方式:散射,它改变了光线的方向;吸收,它将光能吸收并转变为其它形态的能量(如热能)。而散射效果对场景中物体的影响又分为两个方面:一方面是一部分由物体反射的光被散射到视线之外,并不能到达摄像机,因而被衰减,称作外散射;另一方面是一部分太阳光被空气中的粒子散射正对向摄像机,这些正朝向视线的散射被称作内散射。
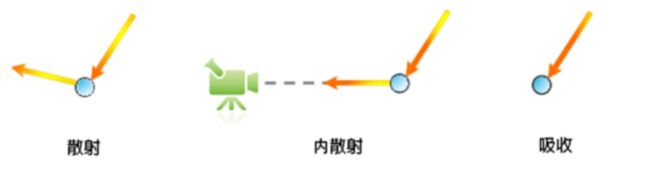
最后抵达视点被人眼所观察到的光线可分为两部分:衰减后的物体反射辐射度、被内散射的大气散射辐照度。
L v i e w e r = L o b j e c t ⋅ e − T ( O → C ) + L i n s c a t t e r L_{viewer}=L_{object}\cdot e^{-T(O\to C)}+L_{inscatter} Lviewer=Lobject⋅e−T(O→C)+Linscatter (7)
其中 L v i e w e r L_{viewer} Lviewer为最终抵达摄像机的总光强, L o b j e c t L_{object} Lobject为物体的反射光(当视线不与物体相交时则为 0 0 0), L i n s c a t t e r L_{inscatter} Linscatter为从O到C点路径上所有内散射光线的总和,这里暂时忽略太阳直射。
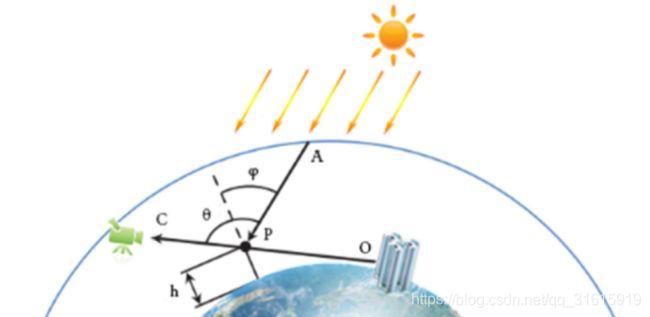
公式(7)中的 e − T ( O → C ) e^{-T(O\to C)} e−T(O→C)是光线从O点到C点的衰减系数,其中 T ( O → C ) T(O\to C) T(O→C)被称作光学深度(Optical Length),它是散射系数与密度乘积在整条路径上的积分。
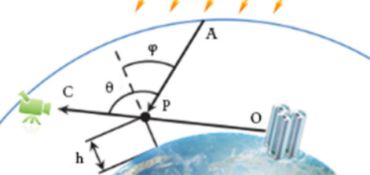
① 光学深度:在上图中,大气层内有一点 P P P,它在视线 C O CO CO上。太阳光线照向地球,在穿过大气层的时候会受空气分子和空气溶胶的散射作用而发生衰减(外散射的影响),最终到达 P P P点处的光能总量为:
L p = L s u n e − T ( A → P ) L_p=L_{sun}e^{-T(A\to P)} Lp=Lsune−T(A→P) (8)
其中 L s u n L_{sun} Lsun是太阳光到达大气层前的初始辐射度。上图中 A A A点是光线到达 P P P点之前与大气层的交点,则 T ( A → P ) T(A\to P) T(A→P)被称作 A A A点到 P P P点的光学深度(Optical Depth),它本质上就是 A A A点到 P P P点这条路径上散射系数乘上空气密度的积分(包含Rayleigh散射与Mie散射):
T ( A → P ) = ∫ A P ( β R e e − h ( t ) H R + β M e e − h ( t ) H M ) d t T(A\to P)=\int_A^P(\beta_R^ee^{-\frac{h(t)}{H_R}}+\beta_M^ee^{-\frac{h(t)}{H_M}})dt T(A→P)=∫AP(βRee−HRh(t)+βMee−HMh(t))dt (9)
公式(9)中的参数前面都已提到过: β R e \beta_R^e βRe即Rayleigh散射系数, β M e \beta_M^e βMe是Mie散射系数,而形如 e − h H e^{-\frac{h}{H}} e−Hh的则分别是Rayleigh散射粒子密度分布函数、Mie散射粒子密度分布函数。在这里我们散射系数当作一个在海平面上的常数值,则式(9)可变为如下形式:
T ( A → P ) = β R e ∫ A P e − h ( t ) H R d t + β M e ∫ A P e − h ( t ) H M d t T(A\to P)=\beta_R^e\int_A^Pe^{-\frac{h(t)}{H_R}}dt+\beta_M^e\int_A^Pe^{-\frac{h(t)}{H_M}}dt T(A→P)=βRe∫APe−HRh(t)dt+βMe∫APe−HMh(t)dt (10)
所以我们只需对AP路径上的空气密度进行积分,这个积分值被称光学长度(Optical Length),直观的意义就是在光线照射的路径上空气粒子的总量。
② 散射系数:散射系数决定了散射介质对光线的散射的强弱程度,也反应了光线在通过该介质时的衰减程度。我们已经在前面提到,Rayleigh散射对不同波长的光线散射强度不同,在实现中我们可以将其在海平面处的散射系数设为一个三维向量:
β R . r g b = ( 5.81 , 13.5 , 33.1 ) × 1 0 − 6 \beta_R.rgb=(5.81,13.5,33.1)\times10^{-6} βR.rgb=(5.81,13.5,33.1)×10−6
而Mie散射对波长的变化影响不明显,所以可以将其在海平面上的散射系数设为标量:
β M . r g b = 2.0 × 1 0 − 5 \beta_M.rgb=2.0\times10^{-5} βM.rgb=2.0×10−5
③ 相位函数:己知入射光能和介质的散射系数,我们就可以计算出有多少光线会被介质散射出去。但并非所有的光线在散射之后都会朝向摄像机,有一部分会被散射到其它方向,无法被肉眼所观察到(称作外散射)。所以为了计算内散射的光线量,还需要有另外一个因子描述这个物理量。而相位函数 p ( θ ) p(\theta) p(θ)则描述了在该点有多少光线散射之后朝向摄像机,其中的参数 θ \theta θ是太阳光到点 P P P的向量 L P LP LP与点 P P P到摄像机位置的向量 P C PC PC的夹角,如下图所示。
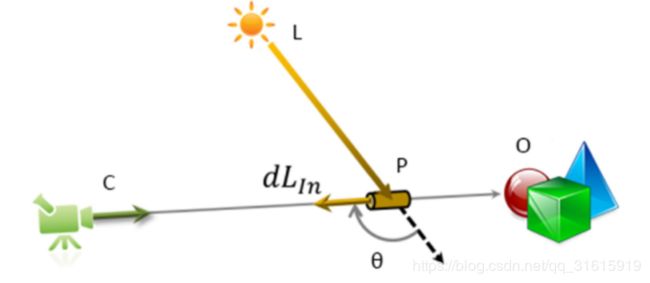
相位函数是标准化的,函数本身在所有方向的积分为 1 1 1。Rayleigh散射特点是各向同性,光线会以介质粒子为中心均匀地向各个方向散射,其相位函数是前面提到的公式(3)。而Mie散射呈现明显的各向异性,光线会被更多的介质粒子向后方散射,其相位函数是前面提到的公式(5)。
④ 单重散射:目前我们讨论的都是单重散射,即太阳光在到达视点之前只会进行一次散射。点 P P P的内散射光在达到视点前还会受到空气颗粒影响而衰减,衰减程度取决于点 P P P到点 C C C(视点)的光学深度 T ( P → C ) T(P\to C) T(P→C),因而衰减因子为 e − T ( P → C ) e^{-T(P\to C)} e−T(P→C)。
所以最终达到视点C的内散射方程如下:
L i n s c a t t e r = ∫ C O L s u n ⋅ e − T ( A ( s ) → P ( s ) ) ⋅ e − T ( P ( s ) → C ) ⋅ ( β R s e − h ( s ) H R p R ( θ ) + β M s e − h ( s ) H M p M ( θ ) ) d s L_{inscatter}=\int_C^OL_{sun}\cdot e^{-T(A(s)\to P(s))}\cdot e^{-T(P(s)\to C)}\cdot (\beta_R^se^{-\frac{h(s)}{H_R}}p_R(\theta)+\beta_M^se^{-\frac{h(s)}{H_M}}p_M(\theta))ds Linscatter=∫COLsun⋅e−T(A(s)→P(s))⋅e−T(P(s)→C)⋅(βRse−HRh(s)pR(θ)+βMse−HMh(s)pM(θ))ds(10)
上式中有两个衰减因子,一个是从 A A A到 P P P的衰减因子,一个是从 P P P到 C C C的衰减因子。整个积分路径是从 O O O到 C C C,这一方程描述了从 O O O到 C C C路径上全部内散射光的总和。
内散射积分公式(10)中,在积分路径OC上太阳光与视线的夹角 θ \theta θ保持不变,因此有必要将相位函数 p ( θ ) p(\theta) p(θ)从积分内部中提取出来。而太阳光是平行光, L s u n L_{sun} Lsun是大阳光在大气层顶层的辐射度,视为常量,也可从积分内部提取出来。散射系数亦如此。故公式(10)可变为如下:
L i n s c a t t e r = L s u n p R ( θ ) β R s ∫ C O e − T ( A ( s ) → P ( s ) ) − T ( P ( s ) → C ) e − h ( s ) H R d s + L s u n p M ( θ ) β M s ∫ C O e − T ( A ( s ) → P ( s ) ) − T ( P ( s ) → C ) e − h ( s ) H M d s L_{inscatter}=L_{sun}p_R(\theta)\beta_R^s\int_C^Oe^{-T(A(s)\to P(s))-T(P(s)\to C)}e^{-\frac{h(s)}{H_R}}ds+L_{sun}p_M(\theta)\beta_M^s\int_C^Oe^{-T(A(s)\to P(s))-T(P(s)\to C)}e^{-\frac{h(s)}{H_M}}ds Linscatter=LsunpR(θ)βRs∫COe−T(A(s)→P(s))−T(P(s)→C)e−HRh(s)ds+LsunpM(θ)βMs∫COe−T(A(s)→P(s))−T(P(s)→C)e−HMh(s)ds (11)
故要计算一个视点到物体之间的内射光线,我们需要对视线路径上每一点的衰减因子以及空气密度进行积分。
⑤ 多重散射:光线在传输过程中被空气中的一个粒子影响,称为光的一次散射。当空气中大颗粒较多时,被粒子散射的光又会被散射方向上的其它粒子再次散射,这个过程称为多重散射(Multiple Scattering)。在晴朗干净的天空中,由于空气中大粒子的数量较少,多重散射的作用不是很明显。而在空气浑浊或黄昏时,多重散射会对场景的真实性产生较明显的影响。
我们前面的讨论都是单一散射模型。这一模型在白天的时候比较合理,这一假设在白天的时候比较合理,因为在白天的时候太阳光强度较高,多重散射作用不明显;而在傍晚的时候,由于太阳直射光强度变弱,多重散射对场景的影响会变得更加重要,在渲染真实图像中必须加以考虑。即便如此,单一散射模型在此时依旧可以提供一个相对较好的结果。
关于多重散射的文献资料较少,因为单重散射模型目前已经有了不错的渲染结果。在我阅读的这篇论文《Precomputed Atmospheric Scattering》中考虑了多重散射的情况,较为复杂,在后面论述。
⑥ 体积光:当光线照射到遮挡物时,一部分光线会从物体的边缘和空隙中穿过,并产生很明显的光柱效果,在视觉上给人以很强的体积感,所以称之为体积光(Light shaft)。体积光在自然界中是十分常见的现象,如太阳光从云隙中透过时产生的云隙光,森林中阳光从树叶中穿过产生的光柱。体积光现象有时又被称作“丁达尔效应”。其理论基础同样是光线的散射原理,可以使用前面描述的Mie散射理论来解释。对于溶胶,其粒子大小通常与可见光的波长相当,所以在光线穿过气溶胶时,会发生明显的Mie散射现象,产生肉眼可观察到的光柱体。

渲染方程及其实现
为了便于论述,我们记 L ( x , v , s ) L(x,v,s) L(x,v,s)为视点 x x x从方向 v v v接收的总的辐射度,其中 s s s是太阳方向向量。记 x 0 ( x , v ) x_0(x,v) x0(x,v)为视线 v v v的终点(通常为地面、物体或大气顶层)。 x x x到 x 0 x_0 x0之间的衰减因子 T T T、 x 0 x_0 x0处的反射辐射度 I I I、在某一点 y y y向 − v -v −v内散射的辐射度 J J J定义如下:
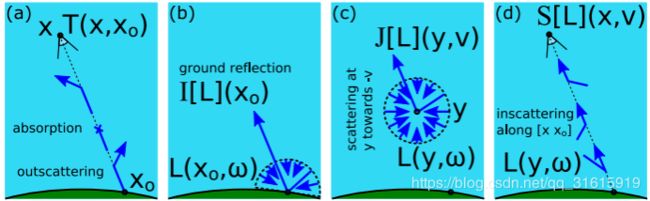
T ( x , x 0 ) = e x p ( − ∫ x x 0 ( β R e ρ R ( y ) + β M e ρ M ( y ) ) d y ) T(x,x_0)=exp(-\int_x^{x_0}(\beta_R^e\rho_R(y)+\beta_M^e\rho_M(y))dy) T(x,x0)=exp(−∫xx0(βReρR(y)+βMeρM(y))dy) (12)
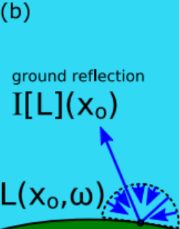
I [ L ] ( x 0 , s ) = α ( x 0 ) π ∫ 2 π L ( x 0 , ω , s ) ⋅ n ( x 0 ) d ω , o r 0 I[L](x_0,s)=\frac{\alpha(x_0)}{\pi}\int_{2\pi}L(x_0,\omega,s)\cdot n(x_0)d\omega ,or 0 I[L](x0,s)=πα(x0)∫2πL(x0,ω,s)⋅n(x0)dω,or0 (13)
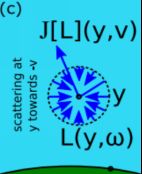
J [ L ] ( y , v , s ) = ∫ 4 π ∑ i ∈ { R , M } β i s ( y ) p i ( v ⋅ w ) L ( y , ω , s ) d ω J[L](y,v,s)=\int_{4\pi}\sum_{i\in\{R,M\}}\beta_i^s(y)p_i(v\cdot w)L(y,\omega,s)d\omega J[L](y,v,s)=∫4π∑i∈{R,M}βis(y)pi(v⋅w)L(y,ω,s)dω (14)
公式(12)、(13)、(14)对应上图的(a)、(b)、(c)。有了以上的函数表示,现在我们可以定义渲染方程了。
1、渲染方程
L ( x , v , s ) = L 0 ( x , v , s ) + R [ L ] ( x , v , s ) + S [ L ] ( x , v , s ) L(x,v,s)=L_0(x,v,s)+R[L](x,v,s)+S[L](x,v,s) L(x,v,s)=L0(x,v,s)+R[L](x,v,s)+S[L](x,v,s) (15)
L 0 ( x , v , s ) = T ( x , x 0 ) L s u m , o r 0 L_0(x,v,s)=T(x,x_0)L_{sum}, or 0 L0(x,v,s)=T(x,x0)Lsum,or0 (16)
R [ L ] ( x , v , s ) = T ( x , x 0 ) I [ L ] ( x 0 , s ) R[L](x,v,s)=T(x,x_0)I[L](x_0,s) R[L](x,v,s)=T(x,x0)I[L](x0,s) (17)
S [ L ] ( x , v , s ) = ∫ x x 0 T ( x , y ) J [ L ] ( y , v , s ) d y S[L](x,v,s)=\int_x^{x_0}T(x,y)J[L](y,v,s)dy S[L](x,v,s)=∫xx0T(x,y)J[L](y,v,s)dy (18)
L ( x , v , s ) L(x,v,s) L(x,v,s)为视点 x x x从方向 v v v接收的总的辐射度。 L 0 L_0 L0是到达 x x x的太阳直射光,因此当视线 v v v与太阳方向向量 s s s不相等时 L 0 L_0 L0为0(又或者太阳被遮挡了)。 R [ L ] R[L] R[L]是在点 x 0 x_0 x0收到的反射的辐射度。 S [ L ] S[L] S[L]则是从 x 0 x_0 x0到 x x x路径上接收的内散射光。从渲染方程可以看出,衰减因子 T T T无处不在,这是因为在大气层内,涉及到光线的传播都要考虑外散射以及光线被吸收的影响。
这个渲染方程计算量非常大,尤其是公式(18),一重积分内部还嵌套了两重积分。纯粹地暴力计算对于实时渲染来说几乎不可能。为了能够实现实时渲染大气层,不少论文提出了查找表的优化思想,这是一种基于预先计算的优化方法。但大多数的论文都只是考虑了单重散射,我阅读的这篇论文《Precomputed Atmospheric Scattering》将多重散射也考虑进去了,提出了一种4维查找表的方法,在后面论述。除此之外,渲染方程也设计到大量的积分计算。为此,我们采用梯形法则和光线步进(Ray Marching)来快速计算数值积分。
下面的叙述部分,由于代码比较繁多,我尽量用伪代码描述。
2、光线衰减因子
前面已经提到过,从 x x x的 x 0 x_0 x0光线衰减因子如下(实际计算中把散射系数提出积分外):
T ( x , x 0 ) = e x p ( − ∫ x x 0 ( β R e ρ R ( y ) + β M e ρ M ( y ) d y ) T(x,x_0)=exp(-\int_x^{x_0}(\beta_R^e\rho_R(y)+\beta_M^e\rho_M(y)dy) T(x,x0)=exp(−∫xx0(βReρR(y)+βMeρM(y)dy)
每一帧去计算它并不现实,因此早在1994年就有人提出了查找表的优化方法。如下图所示,假设我们要计算 p p p到 q q q的衰减因子。 i i i是 p p p点沿视线与大气顶层的交点。则有: p p p到 i i i的衰减因子= p p p到 q q q的衰减因子乘上q到i的衰减因子(这里相乘的原因是决定衰减因子的光学深度是在其公式的指数位置上,衰减因子相乘等于相应的指数相加)。那么 p p p到 q q q的衰减因子= p p p到 i i i的衰减因子除以 q q q到 i i i的衰减因子。因此只要知道点到大气顶层的衰减因子,就可计算任两点之间的光线衰减因子。
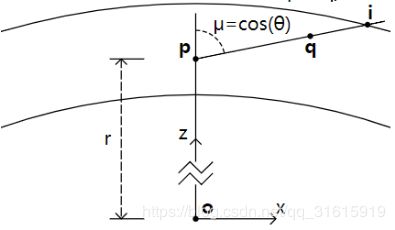
此外,O’ Neil发现了衰减因子的计算取决于两个参数:当前点的高度 r r r和视线的天顶角 θ \theta θ。也就是说我们可以通过预先计算( r r r, θ \theta θ)的全部组合决定的衰减因子存放到一张纹理中,后面的实时计算直接根据需要计算的( r r r, θ \theta θ)查找这张纹理。为了方便,我们取参数( r r r, c o s θ cos\theta cosθ),记 u = c o s θ u=cos\theta u=cosθ。
① 点p到大气顶层的距离:即计算向量 p i pi pi的长度。建立如图所示的坐标系,点 O O O为地心,则向量 p i pi pi距离点 p p p为 d d d的一点坐标( x x x, z z z)为:( d 1 − u 2 d\sqrt{1-u^2} d1−u2, r + d u r+du r+du)
那么设距离 d d d为向量 p i pi pi的长度,则( x x x, z z z)即为点 i i i的坐标。已知大气层半径为 r t o p r_{top} rtop,则由勾股定理有: ( d 1 − u 2 ) 2 + ( r + d u ) 2 = r t o p 2 (d\sqrt{1-u^2})^2+(r+du)^2=r_{top}^2 (d1−u2)2+(r+du)2=rtop2,整理后即为二元一次方程: d 2 + 2 r u d + r 2 = r t o p 2 d^2+2rud+r^2=r_{top}^2 d2+2rud+r2=rtop2,其中 r r r、 u u u和 r t o p r_{top} rtop已知,可求出距离 d d d。同样可通过该二元一次方程的判别式判断是否有解,从判断射线( r r r, u u u)是否与大气层(或地表)存在交点。
点p到地球表面交点的距离同理,将 r t o p r_{top} rtop换成 r b o t t o m r_{bottom} rbottom即可。
② 计算点p到i(与大气顶层的交点)的光学长度:计算衰减因子需要计算点 p p p到 i i i的光学深度,也就是对 p p p到 i i i的散射系数和空气密度乘积进行积分。其中散射系数(包括Rayleigh散射和Mie散射)系数我们取海平面上相应的散射系数,故我们只需对 p p p到 i i i路径的空气密度进行积分,这就是光学长度– ∫ p i ρ ( s ) d s \int_p^i\rho(s)ds ∫piρ(s)ds。
计算积分我们采用梯度法,以光线步进(Ray Marching)循环采样计算累加和。如下图所示,假设我们取 P 1 P_1 P1- P 5 P_5 P5这五个采样点,依次计算每个点的空气密度乘上积分步长,累加计算。

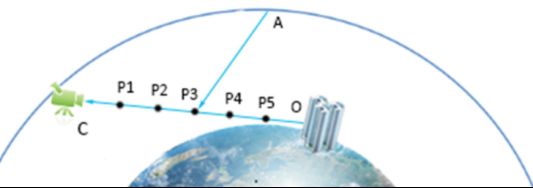
计算Rayleigh光学长度和Mie光学长度均采用以上的方法计算。分别采用以上方法计算之后,再乘上相应的散射系数,就是光学深度,然后衰减因子就按照公式(12)计算即可。
③ 坐标映射:我们把预计算的结果存入一张2D的纹理中,所以需要将( r r r, u u u)映射到纹理坐标( u r u_r ur, v u v_u vu)中。我们知道纹理坐标数值范围是 [ 0 , 1 ] [0,1] [0,1],故对于一个数值 x x x,我们首先要将 x x x映射到 [ 0 , 1 ] [0,1] [0,1],设 x x x的值域为 [ m i n , m a x ] [min,max] [min,max]。则令 x = ( x − m i n ) / ( m a x − m i n ) x = (x-min)/(max-min) x=(x−min)/(max−min),可将其映射到 [ 0 , 1 ] [0,1] [0,1]。
然而值得注意的是,将 x x x映射到 [ 0 , 1 ] [0,1] [0,1]之后,边界部分我们应该要去掉。这是因为我们在对纹理进行查找时需要线性插值,边界部分会产生一些外推值。为了避免这种情况,我们进一步令 x x x(此时 x x x已属于 [ 0 , 1 ] [0,1] [0,1]):
x = 1 2 n + x ∗ ( 1.0 − 1 n ) x=\frac{1}{2n}+x*(1.0-\frac{1}{n)} x=2n1+x∗(1.0−n)1,其中 n n n是纹理的大小, 1 n \frac{1}{n} n1就是一个纹素的大小。如此我们将 x x x由 [ 0 , 1 ] [0,1] [0,1]映射到了 [ 1 2 n , 1 − 1 2 n ] [\frac{1}{2n},1-\frac{1}{2n}] [2n1,1−2n1]上,去掉了边界部分。
接下来我们要将 r r r映射到 u u u,而 u u u映射到 v v v。
对于 r r r,它代表当前点到地心的距离,显然其值域为 [ r b o t t o m , r t o p ] [r_{bottom},r_{top}] [rbottom,rtop]。然而为了更高的精度(避免r接近地表时失真),我们采用了一个非线性映射的方式。如下图所示,实际上对于每个不同 r r r,都对应着一个不同的 ρ \rho ρ,它是视点 p p p到过视点的与地表相切的切线的切点的距离, ρ \rho ρ的最大值则是如下图中的 H H H(最小值为 0 0 0)。故对于 r r r我们采用该映射方式映射到 u r u_r ur: u r = ρ H u_r=\frac{\rho}{H} ur=Hρ。
对于天顶角 u u u,每个特定的天顶角,都对应着不同的距离 d d d(视点到大气顶层交点的距离)。 d d d的下界为 r − r b o t t o m r-r_{bottom} r−rbottom,上界为为 ρ + H \rho+H ρ+H。故其映射方式为: v u = d − d m i n d m a x − d m i n v_u=\frac{d-d_{min}}{d_{max}-d_{min}} vu=dmax−dmind−dmin。
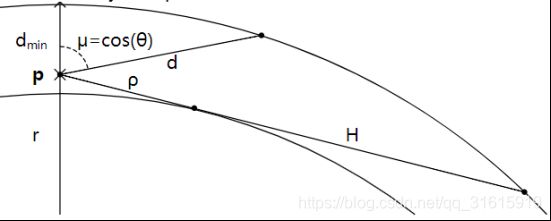

至于计算( ρ \rho ρ, H H H),可以通过两个三角形勾股定理,不再赘述。我们将( r r r, u u u)映射到2D纹理坐标,同样也需要逆过程,这将在预计算阶段用到。逆过程我们将上面的几个公式反推一下即可,也不再赘述。
④ 点p到太阳的光线衰减因子:我们需要计算点 p p p到太阳的光线衰减因子。太阳不是一个点光源,而是一个圆盘发光体。因此 p p p到太阳的光线衰减因子,是以太阳圆盘为区域的衰减因子的积分。在这里我们把太阳圆盘区域上的衰减因子视作相同的常量。故该值等于衰减因子乘上太阳圆盘在水平线上部分占整个圆盘的比例。
设过视点p与地表相切的切线为l。当太阳天顶角 θ s \theta_s θs大于切线l的天顶角 θ h \theta_h θh+太阳的角半径 α s \alpha_s αs时,这部分比例为 0 0 0;当 θ s \theta_s θs小于 θ h − α s \theta_h-\alpha_s θh−αs时为 1 1 1。故我们可以用相应的余弦值来定性地衡量这一比例(注意余弦函数在 [ 0 , π ] [0,\pi] [0,π]递减)。
当 c o s θ s ≤ c o s ( θ h + α s ) ≈ c o s θ h − α s s i n θ h cos\theta_s\leq cos(\theta_h+\alpha_s)\approx cos\theta_h-\alpha_s sin\theta_h cosθs≤cos(θh+αs)≈cosθh−αssinθh时,为 0 0 0;(约等符号是因为 α s → 0 \alpha_s→0 αs→0)
当 c o s θ s ≥ c o s ( θ h − α s ) ≈ c o s θ h + α s s i n θ h cos\theta_s\geq cos(\theta_h-\alpha_s)\approx cos\theta_h+\alpha_s sin\theta_h cosθs≥cos(θh−αs)≈cosθh+αssinθh时,为 1 1 1。
中间部分则用埃尔米特(Hermite)插值,可直接用GLSL的smoothstep函数。
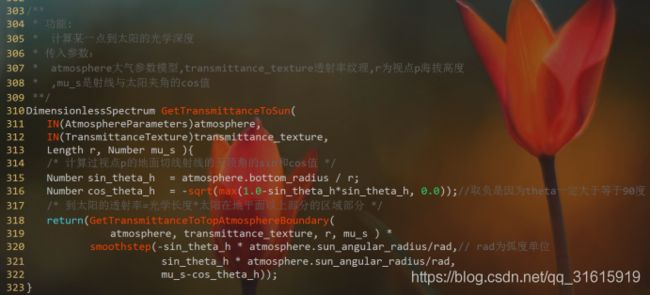
3、单重散射
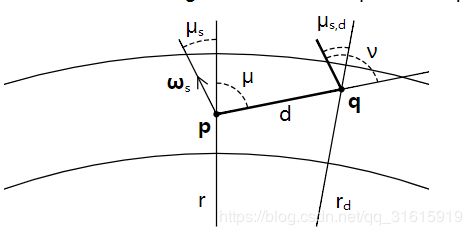
单重散射是指光线在到达视点之前只发生了一次散射。接下来将叙述如何计算单重散射,如何将其映射到3D纹理上。如下图, u u u是视点 p p p处实现的天顶角的 c o s cos cos值,假设太阳到达 q q q点发生了散射, p q pq pq的距离为 d d d, u s u_s us是太阳光方向向量在 p p p处的天顶角 c o s cos cos值, w s w_s ws是太阳光方向向量, v v v是太阳光方向向量与视线 p q pq pq夹角的 c o s cos cos值, u s , d u_{s,d} us,d是太阳光方向向量在 q q q处的天顶角 c o s cos cos值。 r r r是点 p p p到地心的距离, r d r_d rd是点 q q q到地心的距离。
到达p点的内散射辐射度为:
L i n s c a t t e r = ∫ P i L s u n ⋅ e − T ( A ( s ) → P ( s ) ) ⋅ ( β R s e − h ( s ) H R p R ( θ ) + β M s e − h ( s ) H M p M ( θ ) ) d s L_{inscatter}=\int_P^iL_{sun}\cdot e^{-T(A(s)\to P(s))}\cdot(\beta_R^se^{-\frac{h(s)}{H_R}}p_R(\theta)+\beta_M^se^{-\frac{h(s)}{H_M}}p_M(\theta))ds Linscatter=∫PiLsun⋅e−T(A(s)→P(s))⋅(βRse−HRh(s)pR(θ)+βMse−HMh(s)pM(θ))ds
其中的 L s u n L_{sun} Lsun和两个相位函数我们先不管,计算内散射辐射度我们需要多p到大气顶层交点之间对光线衰减因子和空气密度进行积分。以上图积分点 q q q为例,我们需要 q q q到太阳的光线衰减因子、 p p p到 q q q的光线衰减因子,而这两个值可直接借助查找我们前面已经计算好的纹理获得。故对一个积分采样点,其积分函数值计算的伪代码如下。

① 内散射积分:同样地,我们采用梯度法和光线步进法进行积分。积分路径的终端实际上不一定是大气顶层,有可能是地表,但积分过程都是一样。

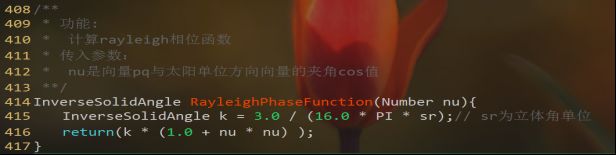
② 相位函数:对于Rayleigh相位函数和Mie相位函数,直接分别套用公式(3)和公式(5)。
③ 坐标映射:计算单重散射积分同样非常耗费性能。因此我们一样使用预计算查找表的方法计算单重散射积分。与光线衰减因子不同的是,单重散射积分取决于四个参数,就是前面提到的( r r r, u u u, u s u_s us, v v v),这意味着我们需要将这四个参数映射到4D纹理坐标。
对于 ( r , u ) (r,u) (r,u)的坐标映射,与前面的提到的映射方法相同,这里不再赘述。
对于 v v v,其值域为 [ − 1 , 1 ] [-1,1] [−1,1],我们做简单的线性映射,令 u v = 1 + v 2 u_v=\frac{1+v}{2} uv=21+v。
对于 u s u_s us,通过非线性映射,如下所示(原因不明):
a = d − d m i n d m a x − d m i n a=\frac{d-d_{min}}{d_{max}-d_{min}} a=dmax−dmind−dmin, A = − 2.0 u s m i n r b o t t o m d m a x − d m i n A=\frac{-2.0u_{s_min}r_{bottom}}{d_{max}-d_{min}} A=dmax−dmin−2.0usminrbottom, u u s = m a x ( 1.0 − a A , 0.0 ) 1.0 + a u_{u_s}=\frac{max(1.0-\frac{a}{A},0.0)}{1.0+a} uus=1.0+amax(1.0−Aa,0.0)
而逆过程则直接根据上述公式倒推即可。现在我们把( r r r, u u u, u s u_s us, v v v)映射到了4D纹理坐标,然而实际上纹理维度最多3D。故映射到4D之后,我们还要将4D坐标映射到3D坐标。为此,我们可通过取整、取模来实现。
4、多重散射
在考虑多重散射的时候,渲染方程就变为:
L = L 0 + L 1 + L 2 + . . . = L 0 + L ∗ L=L_0+L_1+L_2+...=L_0+L_* L=L0+L1+L2+...=L0+L∗ (18)
其中 L i L_i Li代表光线散射 i i i重。事实上,在白天的时候多重散射的效果微乎其微,而在傍晚的时候效果较为明显一点。因此实现多重散射是性价比非常低的事情,计算量比单重散射多很多,但是渲染的提升效果可以说是非常小了。
多重散射的来源有两个:一个是经过 ( n − 1 ) (n-1) (n−1)次散射之后再发生了一次散射,而另一个是从地面的反射的光线。在这里我们先暂时不讨论地面的反射。多重散射可以分解成 2 2 2重散射、 3 3 3重散射、 4 4 4重散射…等等 n n n重散射的累加和。而且,第 i i i重散射可以根据第 i − 1 i-1 i−1重散射计算得到。
先讨论视点 p p p接收到的第 n n n重散射,设视点 p p p沿视线 v v v的终端为 i i i, q q q为路径 p i pi pi上的任意一点。对于 q q q点,我们要计算 q q q点接收的经过 n − 1 n-1 n−1重散射(第 n n n重散射时发生内散射,射向视点)的辐射度,这需要对整个球体方向进行积分,是二重积分的计算量。然后我们需要对路径 p i pi pi上所有的 q q q点( q q q点是 p i pi pi上的一点)进行积分,是一重积分的计算量。由此我们可以知道,计算第 n n n重散射,一重积分里面嵌套了两重积分,为三重积分的计算量。如果对于每一重散射的计算,都从头开始的话,这必然导致很大的计算量,而且有不少重复的计算。
为此,对于多重散射,我们采用迭代的方式来一重一重地计算,而且同样采用查找表的优化方法。每计算一重散射,我们把结果存储到纹理中,然后下一重的散射计算就直接查找这个纹理。如此,我们通过迭代的方式避免前一重的散射计算。
然而即便如此,以三重积分的方式计算第n重散射依然存在着不少重复的部分。如下图所示,设 L L L为 q q q点接收的经过 n − 1 n-1 n−1重散射最后第 n n n重散射到 − w -w −w方向的总的光线辐射度。如果以三重积分计算 n n n重散射,那么在 p p p点和 p ’ p’ p’点都会重复地计算到 L L L。事实上,对于 p p p点到 q q q点之间所有的点,都会重复地计算 L L L。显然,为了性能考虑,我们必须避免这一重复的部分。以空间换时间是个不错的方法。
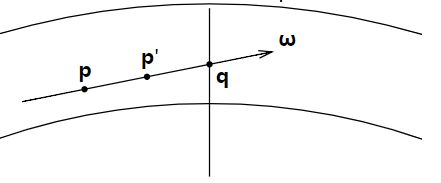
最终,对于计算 n n n重散射我们分两步走:
第一步:对于 p p p点沿视线 w w w上的每一个点 q q q,我们计算 q q q点接收的经过 n − 1 n-1 n−1重散射的辐射度,这需要两重积分;
第二步:在 p p p点沿视线 w w w的路径上,计算第 n n n重散射,我们查找第一步计算得到的纹理,这只需单重积分。
① 第一步:计算 q q q点接收的经过 n − 1 n-1 n−1重散射的光线(第 n n n重散射射向 − w -w −w)。
如下所示,对于所有可能的方向 w i w_i wi,我们需要计算从 w i w_i wi方向接收的入射辐射度 L i L_i Li。 L i L_i Li由两部分组成:一部分是 n − 1 n-1 n−1重散射的辐射度(可以直接查找 n − 1 n-1 n−1重散射的纹理得到);另一部分是当射线 w i w_i wi与地面相交时,我们需要考虑地面的反射辐射度。
n − 1 n-1 n−1重散射辐射度由前面的迭代计算得到,不再讨论。我们需要重点讨论的是地面的反射辐射度。设射线( q q q, w i w_i wi)与地面的交点为 r r r,那么从地面接收的反射辐射度应该是以下几项的乘积:
-
点 q q q和点 r r r之间的光线衰减因子;
-
地面的平均反照率;
-
地面的Lambertian BRDF函数的 1 / π 1/\pi 1/π;
-
地面接收的经过 n − 2 n-2 n−2次散射辐照度,这是个半球方向的积分,我们将在后面讨论,现在假设我们已经可以计算得到。

② 第二步:第二步就是利用第一步的计算结果进行单次积分。在 p p p点沿视线 w w w的路径上,计算第 n n n重散射,我们查找第一步计算得到的纹理。对于 p p p到边界交点的每一个点 q q q,设 q q q计算得到的 n − 1 n-1 n−1重散射密度为 L L L,则由 q q q到 p p p的辐射度应该再乘上一个 q q q到 p p p之间的光线衰减因子。
同样的,我们采用梯度法和光线步进计算 p p p到边界路径上的黎曼和。

③ 坐标映射:与单重散射一样。
5、地面辐照度
地面接收的辐照度是直接辐照度、单重散射或多重散射之后接收的辐照度总和,我们分为直接辐照度和间接辐照度。计算地面接收的辐照度有以下两个目的:
-
计算 n n n重散射的时候,我们需要考虑从地面反射的辐射度;
-
渲染地面的需要。
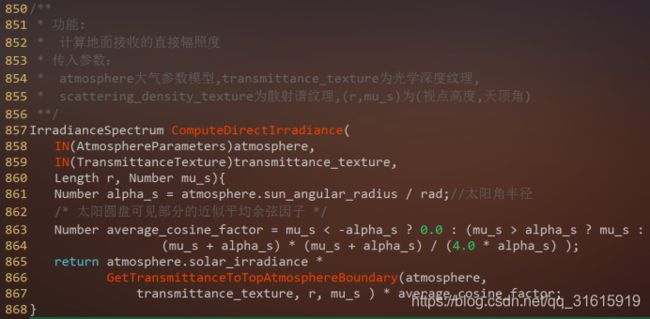
① 直接辐照度:太阳光线直达地面,中间不发生的散射(但是会向外散射导致光强减弱),所以我们将太阳的辐射度乘上地面到大气顶层的光线衰减因子即可。同时,值得注意的是太阳是一个圆盘,我们还需要考虑太阳可见圆盘的比例,这在前面已经讨论过了。比较简单,直接贴代码了。
② 间接辐照度:间接辐照度考虑单重及多重散射,如下所示,我们需要对以地面法线为轴向的半球方向进行积分。

5、预计算
有了以上的铺垫,我们现在可以将光线衰减因子、单重散射、多重散射以及地面辐照度预先计算到纹理中,然后渲染的时候直接根据相应的参数去查找纹理(需要纹理坐标的映射)从而获取相应的值,如此在渲染时省去了大量的计算,这带来了非常大的性能提升。

实验结果
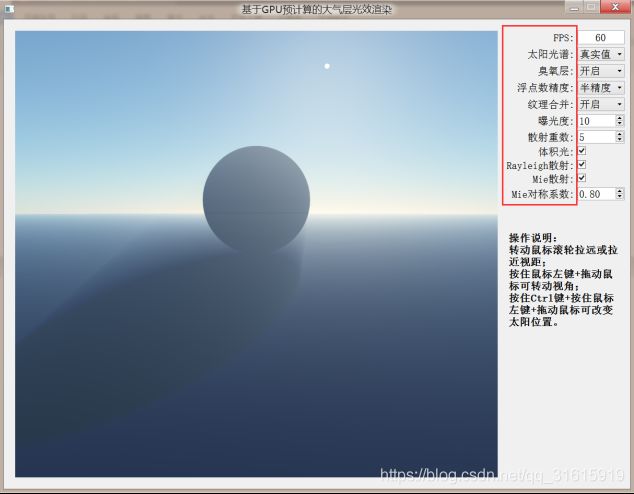
演示的是一个非常简单的场景,地球以及地球表面上的球体。由于仅仅只有两个球体,那么绘制轮廓部分用光线追踪的办法是非常简单的,而且在片元着色器也很容易实现,只需求解几个二元一次方程即可。而光照部分则是查找前面已经计算好的散射纹理。
① 实验平台:
-
操作系统: Windows8.1
-
IDE: Qt Creator
-
语言: C++
-
API: OpenGL3.3+, Qt 5.7
② 可调参数:
-
太阳光谱:选择常量值还是真实值(通过真实的太阳光谱线性插值)
-
臭氧层:是否开启臭氧层(臭氧层也会吸收一部分光线)
-
散射重数:最低为 1 1 1(即只考虑单重散射)
-
体积光:是否开启丁达尔效应
-
Rayleigh散射:是否开启rayleigh散射
-
Mie散射:是否开启Mie散射
③ 实验结果:
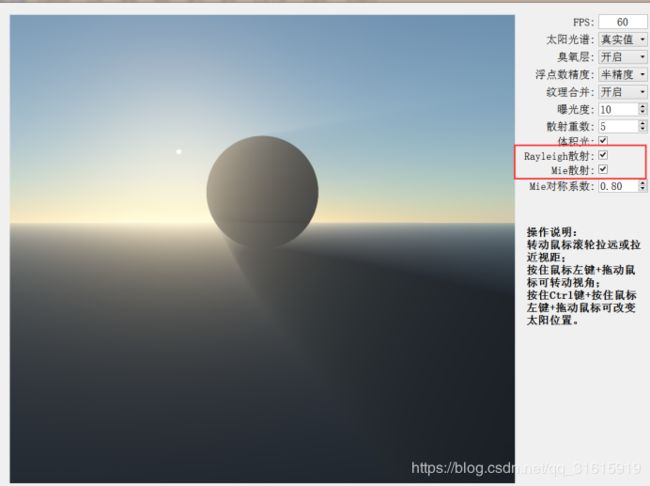
1)、首先,把Rayleigh散射和Mie散射都关闭了,也就是说相当于没有大气层的存在,和月球上的情况相似,所以天空不再是蓝色而是黑色(直接看到外太空了),太阳周围也不会出现光晕。而且由于没有散射,那么阴影部分(非太阳直射的地方)将完全漆黑。
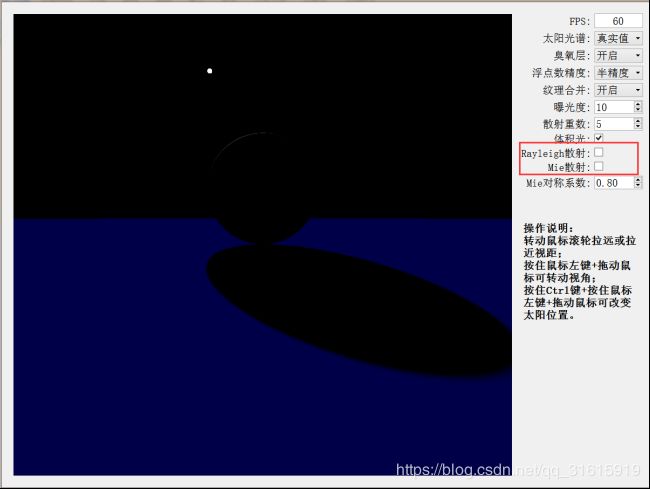
3)、仅开启Rayleig散射,这时由于没有Mie散射,也就是我们剔除了气溶胶的作用,天空的朦胧感降为 0 0 0,天空看着很清澈,这与我们的生活经验一致。

4)、而如果仅开启Mie散射,那么天空不会呈现蓝色,而是呈现如下情况。可以看出,Mie散射呈现的是一种丁达尔效应的朦胧感。

5)、单重散射、多重散射的对比。实现的最大难度在于多重散射,需要编写大量的代码,而且占用更多的空间,但是提升的效果其实很小。如下图。

对比上面的几张图,可以看到其实单重散射的效果已经非常不错了。而且散射重数多了其实区别也不大。
6)、体积光效果:体积光效果是大气光效渲染比较复杂的一个方面,但是实现的话看起来是很令人震撼的。遗憾的是,论文作者提出的体积光实现是基于阴影体的,简单场景没什么问题,但是比较复杂的就不太现实了。

7)、Mie散射对称系数:控制Mie散射的方向性,为正则向后散射,为负则向前散射。为正时越大向后散射得越多。

9)、一些从外太空观察的效果。

此外,值得注意的是,渲染的速度非常快,FPS稳定在 60 60 60。基于预先计算的查找表的优化方法把渲染时大量的计算挪到程序启动的初始阶段,而且开始阶段耗费时间也不多,最多两三秒。对于散射重数低于 10 10 10的,几乎是秒开。
参考文献
1、《Precomputed Atmospheric Scattering》
2、《SIGGRAPH 2009 - Lighting Research at Bungie》
3、《基于GPU的实时大气散射渲染优化算法研究与实现_方辰》
4、《PreethamSig2003CourseNotes》
5、《数字地球大气散射的GPU实现》
6、《基于GPU的行星大气散射效果实时渲染技术研究_刘维敏》
7、《基于GPU的地球大气散射现象可视化仿真_杜芳》
8、《多重散射的天空光照效果建模与实时绘制_艾祖亮》