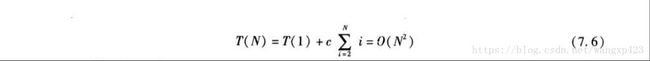快速排序算法（Java）

一，快速排序

快速排序，是实践中的一种快速的排序算法，在C++和java基本类型的排序中特别有用，它的平均运行时间是O(NlogN)。该算法之所以特别快，主要是由于非常精炼和高度优化的内部循环。它的最坏情形性能为O(N²)，但经过少许努力可使这种情形极难出现，通过将快速排序和堆排序结合，由于堆排序的O(NlogN)最坏情形运行时间，我们可以对几乎所有的输入都能达到快速排序的快速运行时间。

二，分割策略

此处描述的分割策略已经被证明能够给出好的结果，我们将会看到，分割是一种很容易出错或者低效的操作，但使用一种已知方法是安全的。该法的第一步是通过将枢纽元(锚点)与最后的元素交换使得枢纽元离开要被分割的数据段。i从第一个元素开始而j从倒数第二个元素开始，如果原始输入与前面的一样，那么下面的图表示当前的状态(6是枢纽元)

暂时假设所有元素互异，后面我们将着重考虑在出现重复元素时该怎么办，作为有限的情况，如果所有的元素都相同，那么我们的算法必须做该做的事。

在分割阶段，我们要做的就是将所有小元素一定到枢纽元的左边而把大的元素移动到它的右侧。

当i在j的左边的时候，我们将i右移，移过哪些小于枢纽元的元素，并将j左移，移过哪些大于枢纽元的元素。当i,j停止的时候，i指向一个大元素而j指向一个小元素，如果i在j的左边，那么将两个元素互换，其效果是吧一个大元素推向右边，而将一个小元素推向左边，在上图的例子中，i不移动，而j划过一个位置，情况如下图

在最后一步当枢纽元与i所指向的元素交换的时候，我们知道在位置p小于i的每一个元素都必然是小元素，这是因为或者位置P包含一个从它开始移动的小元素或者位置P上原来的大元素在交换期间被置换了，类似的论断指出，在位置p>i上的元素必然都是大元素。

三，小数组

对于很小的数组(N<=20)，快速排序不如插入排序。不仅如此，因为快速排序是递归的，所以这样的情形经常发生，通常的解决方法是对于小的数组不使用递归的快速排序，而代之以诸如插入排序这样的对小数组更有效的排序算法，使用这种策略实际上可以节省大约15%的运行时间。一种好的截止范围是N=10，虽然在5到20之间任一截止范围都可能产生类似结果，这种做法也避免了一些有害的退化情形。

四，实际的快速排序例程

以下例程来自于《数据结构和算法分析java第三版》

package com.xp.java.sort;

import java.util.Arrays;

/**
 * @类描述：快速排序
 * @创建人：Wangxp
 */
public class QuickSort {
    private static final int CUTOFF = 3;

    /**
     * Quicksort algorithm.
     *
     * @param a an array of Comparable items.
     */
    public static super AnyType>> void quicksort(AnyType[] a) {
        quicksort(a, 0, a.length - 1);
    }

    /**
     * Internal quicksort method that makes recursive calls.
     * Uses median-of-three partitioning and a cutoff of 10.
     *
     * @param a     an array of Comparable items.
     * @param left  the left-most index of the subarray.
     * @param right the right-most index of the subarray.
     */
    private static super AnyType>> void quicksort(AnyType[] a, int left, int right) {
        if (left + CUTOFF <= right) {
            AnyType pivot = median3(a, left, right);

            // Begin partitioning
            int i = left, j = right - 1;
            for (; ; ) {
                while (a[++i].compareTo(pivot) < 0) {
                }
                while (a[--j].compareTo(pivot) > 0) {
                }
                if (i < j)
                    swapReferences(a, i, j);
                else
                    break;
            }

            swapReferences(a, i, right - 1);   // Restore pivot

            quicksort(a, left, i - 1);    // Sort small elements
            quicksort(a, i + 1, right);   // Sort large elements
        } else  // Do an insertion sort on the subarray
            insertionSort(a, left, right);
    }

    /**
     * Method to swap to elements in an array.
     *
     * @param a      an array of objects.
     * @param index1 the index of the first object.
     * @param index2 the index of the second object.
     */
    public static  void swapReferences(AnyType[] a, int index1, int index2) {
        AnyType tmp = a[index1];
        a[index1] = a[index2];
        a[index2] = tmp;
    }

    /**
     * Return median of left, center, and right.
     * Order these and hide the pivot.
     */
    private static super AnyType>> AnyType median3(AnyType[] a, int left, int right) {
        int center = (left + right) / 2;
        if (a[center].compareTo(a[left]) < 0)
            swapReferences(a, left, center);
        if (a[right].compareTo(a[left]) < 0)
            swapReferences(a, left, right);
        if (a[right].compareTo(a[center]) < 0)
            swapReferences(a, center, right);

        // Place pivot at position right - 1
        swapReferences(a, center, right - 1);
        return a[right - 1];
    }

    /**
     * Internal insertion sort routine for subarrays
     * that is used by quicksort.
     *
     * @param a     an array of Comparable items.
     * @param left  the left-most index of the subarray.
     * @param right the right-most index of the subarray.
     */
    private static super AnyType>> void insertionSort(AnyType[] a, int left, int right) {
        for (int p = left + 1; p <= right; p++) {
            AnyType tmp = a[p];
            int j;
            for (j = p; j > left && tmp.compareTo(a[j - 1]) < 0; j--)
                a[j] = a[j - 1];
            a[j] = tmp;
        }
    }

    public static void main(String[] args) {
        Integer[] array = new Integer[]{34, 8, 64, 51, 32, 21};
        quicksort(array);
        System.out.println(Arrays.toString(array));
    }
}

五，快速排序的分析

六，小结

下面给出快速排序的另一种便于理解的写法

    //下面是另外一种写法
    public static void quickSort(int[] a) {
        if (a.length > 0) {
            quickSort(a, 0, a.length - 1);
        }
    }

    private static void quickSort(int[] a, int low, int high) {
        //1,找到递归算法的出口
        if (low > high) {
            return;
        }
        //2, 存
        int i = low;
        int j = high;
        //3,key
        int key = a[low];
        //4，完成一趟排序
        while (i < j) {
            //4.1 ，从右往左找到第一个小于key的数
            while (i < j && a[j] > key) {
                j--;
            }
            // 4.2 从左往右找到第一个大于key的数
            while (i < j && a[i] <= key) {
                i++;
            }
            //4.3 交换
            if (i < j) {
                int p = a[i];
                a[i] = a[j];
                a[j] = p;
            }
        }
        // 4.4，调整key的位置
        int p = a[i];
        a[i] = a[low];
        a[low] = p;
        //5, 对key左边的数快排
        quickSort(a, low, i - 1);
        //6, 对key右边的数快排
        quickSort(a, i + 1, high);
    }

对于快速排序的理解，建议可以使用上面的代码进行断电调试一步一步看交换的过程。更容易理解快速排序。

另一篇：插入排序(java)
本篇中分析部分出自《数据结构与算法分析-java语言结构第三版》