算法导论 第23章 KrusKal算法 Prim算法

终于写出来了 ，这个算法的准备工作也忒多了，先打好图的结构的基础，然后写一个实现不相交集合的数据结构，然后结合这两个结构完成这个算法。

写了两天，终于把这些都解决了，今天终于出来成果了，好激动，好\(≧▽≦)/，忍不住欢呼雀跃，功夫都没白费，不枉费我这星期六日还在写，嘿嘿~~~~~

图的最小生成树算法两种算法，一个是kruskal，一个是Prim

1） Kruskal思路很简单，

1、最开始时，每个结点都看成一棵树，使每个结点都成为一个集合，这个不相交集合我写了个arrayset结构，是基本的数组结构，代码已经在前面的文章中“不想交集的 数组表示法”中给出，只是这里将arrayset中数组的内容变为图的每个结点，类型为VertexNode。

2、使这个图的边按照权重大小排列，我又重写了个结构arcLine（是不是不用重写？我还木有想到，所以就写了。。。），这个还折腾了好久。（发现其实可以重用邻接表的邻接边的结构，存进一个vector,写排序准则，然后排序，都差不多了~~）

3、然后依次遍历每条边，看是否这条边两边的结点是否处于一个集合中（用arrayset的findset判断），如果不在一个集合中，则加入最小树中，并且将这两个集合合并（使用arrayset的unionset），否则，则忽略。

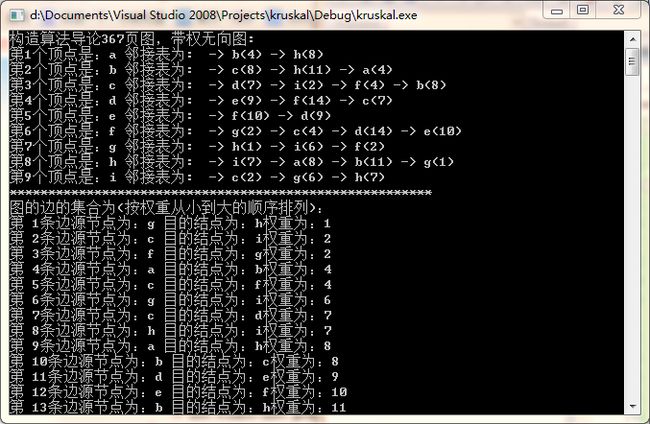
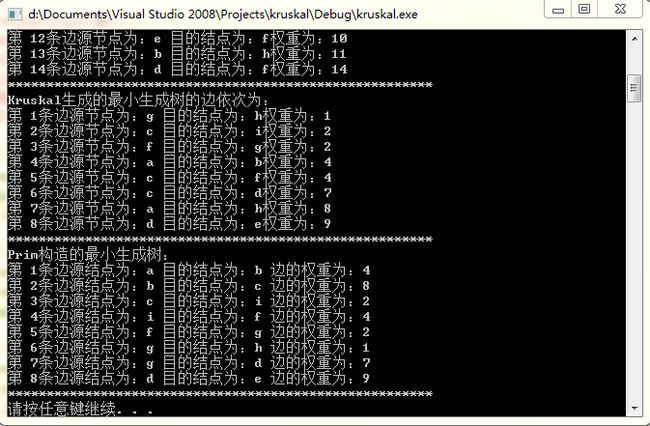
图和程序的运行如下：

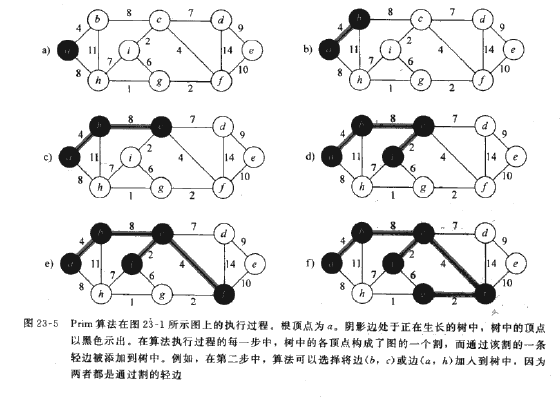
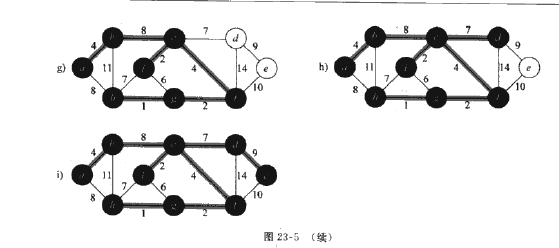
2）Prim算法所具有的性质是集合A（最小生成树的集合）的边总是构成一棵树，这棵树从任意一个根结点r出发，一直长大到覆盖V（顶点集）中的所有结点为止。算法每一部在连接A与A之外的结点所有边中选择一条轻量级边（权重最小的边）加入到A中。算法终止时形成一棵最小生成树。

在算法每一步，就决定了图的一个切割，每次横跨该切割的一条轻量级边被加入树中。

最开始时A = Φ，将所有的顶点存放在一个基于key属性的最小优先队列Q中，

关于这个优先队列的实现，不能直接用priority_queue,因为中间会改变key值，所以每次遍历过出队结点的邻接点后，要将这个优先队列，重新调整，使其变成一个堆，

所以我的解决办法是，直接使用stl的heap算法，而将结点的指针存储到一个vector中，使这个vector成为一个堆，重要的是要在每次key变化之后重新make_heap一下。。

对于堆的排序准则，需要自己写一个仿函数，是按照结点的key值进行排列。

对于每个结点v，属性v.key保存的是连接v和树中结点的所有边中最小边的权重。如果不存在，则为INT_MAX(今天发现可能有溢出，所以将可以将这个值改小一些), 最开始时，除了选定根结点的key会被置为0之外，其余都是最大值，因为现在结点还不存在和树中结点的最小权重边（还没有连接）。

还有一个属性是p,是结点v在树中的父节点。

算法中，当队列不空时，将队列中一个最小结点u出队（即将（u，u.p）加入最小生成树中），然后遍历u的邻接点，当它的邻接点还在Q中，且w（u, v） < v.key（因为key保存的是连接树中结点的最小权值）,将v的父节点变成u，更新v.key为w(u, v)，循环，当队列空时即构成了最小生成树。

以下为过程：

以下为代码：ALgraph.h也是前面的写的图的邻接表表示法稍微改了点，加了个边集~~~~

/************************************************************
 ALGraph: 图的结构 图的操作
 存储为邻接表，多加了一个边的集合arcs
 Date: 2013/12/29
 Author: searchop
************************************************************/

#ifndef ALGRAPH_H
#define ALGRAPH_H

#include 
#include 
#include 
#include 
#include 
#include 
#include "ArraySet.h"
using namespace std;

struct ArcLine          //每条边的结构
{
	int source;         //边的源结点
	int dest;           //边的目的结点
	int weight;         //边的权重
};

//一般将关系运算符重载为非成员函数
bool operator==(const ArcLine& arc1, const ArcLine& arc2)
{
	return arc1.source == arc2.dest && arc1.dest == arc2.source;
	/*&& weight == arc.weight;*/
}

//一般将关系运算符重载为非成员函数
bool operator!=(const ArcLine& arc1, const ArcLine& arc2)
{
	return !(arc1 == arc2);
	/*&& weight == arc.weight;*/
}

//一般将关系运算符重载为非成员函数
bool operator<(const ArcLine& arc1, const ArcLine& arc2)
{
     return arc1.weight < arc2.weight;
}

/*******************************************************/
/*暂时没用到
//比较仿函数
class ArcLineCompare
{
public:
	bool operator()(const ArcLine& arc1, const ArcLine& arc2)
	{
         return arc1.weight < arc2.weight;
	}
};

//相等仿函数
class equalArcLine
{
public:
	bool operator()(const ArcLine& arc1, const ArcLine& arc2)
	{
		return arc1.source == arc2.dest && arc1.dest == arc2.source;
	}
};

//弧的排序准则，用于sort
bool lessArcLine(const ArcLine &arc1, const ArcLine &arc2)
{
	return arc1.weight < arc2.weight;
}
*/
/*****************************************************************/

//邻接表的结构
struct ArcNode          //表结点
{
	int source;        //图中该弧的源节点
	int adjvex;        //该弧所指向的顶点的位置
	ArcNode *nextarc;  //指向下一条弧的指针
	int weight;         //每条边的权重
};

template 
struct VertexNode           //头结点
{
	VertexType data;    //顶点信息
	ArcNode *firstarc;  //指向第一条依附于该顶点的弧的指针
	int key;            //Prim:保存连接该顶点和树中结点的所有边中最小边的权重; 
                        //BellmanFord:记录从源结点到该结点的最短路径权重的上界
	VertexNode *p;      //指向在树中的父节点
	int indegree;       //记录每个顶点的入度
};

template 
bool operator< (const VertexNode& vn1, const VertexNode &vn2)
{
	return vn1.key < vn2.key;
}

template 
bool operator> (const VertexNode& vn1, const VertexNode &vn2)
{
	return vn1.key > vn2.key;
}

template 
bool operator== (const VertexNode& vn1, const VertexNode &vn2)
{
	return vn1.data == vn2.data && vn1.firstarc == vn2.firstarc
		&& vn1.key == vn2.key && vn1.p == vn2.p;
}

//图的操作
template 
class ALGraph
{
public:
	typedef VertexNode VNode;
	ALGraph(int verNum) : vexnum(verNum), arcnum(0)
	{
		for (int i = 0; i < MAX_VERTEX_NUM; i++)
		{
			vertices[i].firstarc = NULL;
			vertices[i].key = INT_MAX/2;
			vertices[i].p = NULL;
			vertices[i].indegree = 0;
		}
	}

	//构造图，进行选择
	void Create()
	{
		InitVertics();
	}

	//构造算法导论367页图，带权无向图
	void CreateWUDG()
	{
		cout << "构造算法导论367页图，带权无向图: " << endl;
        for (int i = 0; i < vexnum; i++)
        {
			vertices[i].data = 'a'+i;
        }

		insertArc(0, 1, 4);
		insertArc(0, 7, 8);
		insertArc(1, 2, 8);
		insertArc(1, 7, 11);
		insertArc(2, 3, 7);
		insertArc(2, 8, 2);
		insertArc(2, 5, 4);
		insertArc(3, 4, 9);
		insertArc(3, 5, 14);
		insertArc(4, 5, 10);
		insertArc(5, 6, 2);
		insertArc(6, 7, 1);
		insertArc(6, 8, 6);
		insertArc(7, 8, 7);

		insertArc(1, 0, 4);
		insertArc(7, 0, 8);
		insertArc(2, 1, 8);
		insertArc(7, 1, 11);
		insertArc(3, 2, 7);
		insertArc(8, 2, 2);
		insertArc(5, 2, 4);
		insertArc(4, 3, 9);
		insertArc(5, 3, 14);
		insertArc(5, 4, 10);
		insertArc(6, 5, 2);
		insertArc(7, 6, 1);
		insertArc(8, 6, 6);
		insertArc(8, 7, 7);

		initArcs();
		/*displayArcs();*/
		/*displayArcs1();*/
	}

	//返回结点
	VNode* getVertexNode(int i)
	{
         return &vertices[i-1];
	}

	//返回边
	ArcLine* getArcLine(int i)
	{
         return &arcs[i-1];
	}

	//打印邻接链表
	virtual void displayGraph()
	{
		for (int i = 0; i < vexnum; i++)
		{
			cout << "第" << i+1 << "个顶点是：" << vertices[i].data
				<< " 顶点的入度为：" << vertices[i].indegree << " 邻接表为: ";
			ArcNode *arcNode = vertices[i].firstarc;
			while (arcNode != NULL)
			{
				cout << " -> " << vertices[arcNode->adjvex].data
					<< "(" << arcNode->weight << ")";
				arcNode = arcNode->nextarc;
			}
			cout << endl;
		}
		cout << "*******************************************************" << endl;
	}

	//打印图的边集
	void displayArcs()
	{
		cout << "图的边的集合为(按权重从小到大的顺序排列)：" << endl;
		vector::iterator it;
		
		int i = 0;
		for (it = arcs.begin(); it != arcs.end(); it++)
		{
			cout << "第 " << i+1 << "条边源节点为：" << vertices[it->source].data 
				<< " 目的结点为：" << vertices[it->dest].data 
				<< "权重为：" << it->weight << endl;
			i++;
		}
		cout << "*******************************************************" << endl;
	}

	//kruskal算法构造最小生成树
	vector &KRUSKAL()
	{
		//这个集合表示最后的生成树
		vector arcvec;
		//这个不相交集合判断结点是否属于同一个集合
		ArraySet > aset(9);

		//使每个结点成为一个单独的集合（变成一个aset中vec数组中的一个元素）
		for (int i = 0; i < vexnum; i++)
		{
			aset.MakeSet1(vertices[i]);
		}

		//依次遍历图的没条边，用aset判断边两边的结点是否属于一个集合，不属于则将其
		//加入最小生成树，并且使这两个结点并为一个集合
		for (int i = 0; i < arcnum/2; i++)
		{
			ArcLine *arc = &arcs[i];
			if (aset.FindSet(aset.getNode(arc->source)) 
				!= aset.FindSet(aset.getNode(arc->dest)))
			{
				arcvec.push_back(*arc);
				aset.UnionSet(aset.getNode(arc->source), aset.getNode(arc->dest));
			}
		}

		cout << "Kruskal生成的最小生成树的边依次为：" << endl;
		for (int i = 0; i < arcvec.size(); i++)
		{
			cout << "第 " << i+1 << "条边源节点为：" << vertices[arcvec[i].source].data 
				<< " 目的结点为：" << vertices[arcvec[i].dest].data
				<< "权重为：" << arcvec[i].weight << endl;
		} 
		cout << "*******************************************************" << endl;
		return arcvec;
	}

	//PVnode排序准则
	class PVNodeCompare
	{
	public:
		bool operator() (VNode *pvnode1, VNode *pvnode2)
		{
			return pvnode1->key > pvnode2->key;
		}
	};

	/***************************************************************************
	关于算法中优先队列的实现，队列中存放的是指向结点的指针，所以可以随着数组的改变而改变。
	因为顶点数组中的值，会一直变化，所以直接用priority_queue会产生invalid heap错误
	(可能是这个堆的实现要去内容能改变，除非当结点数组中有一个改变后，重新把队列清空，所有元素再进队列一次，
	这个应该可以，木有实现，但是根我的解决方法中思想是一致的，即原数组改变后，重新对堆调整一下)，
	但直接运用堆算法make_heap, pop_heap算法实现vector数组中保存的堆的内容，其实是一样的
	即虽然在pop时，原堆会重新调整，但调整只是将第一个元素与最后一个元素调换，然后调整第一个元素使其成为一个堆，
	但是此时堆中其他结点的内容已经改变了，它并没有调整其他结点使全部数组成为一个正确的堆，所以pop后调用一次
	make_heap算法，使这个内容已经改变的数组调整为一个堆！
	原来根本原因是pop中只调整了一个元素，并不管其他元素！dijkstra也一样！（T_T）终于明白了
	****************************************************************************/
	//Prim算法构造最小生成树
	void PRIM(int i)
	{
		vertices[i-1].key = 0;    //将选定结点的key设为0，以便选出第一个出队的元素

		//greater建立的是小顶堆，less即默认为大顶堆
		vector qvnode;   //应该建立以key为键的小顶堆
		for (int i = 0; i < vexnum; i++)
		{
			qvnode.push_back(&(vertices[i])); //将结点的指针依次进队，并形成一个小顶堆
		}
		make_heap(qvnode.begin(), qvnode.end(), PVNodeCompare());
		vector vv;     //保存依次出队的结点
		int arci = 0;

		cout << "Prim构造的最小生成树：" << endl;
		while (qvnode.empty() == false)
		{
			VNode node = *(qvnode.front());     //选择一个队列中key最小的结点
			pop_heap(qvnode.begin(), qvnode.end(), PVNodeCompare());
			qvnode.pop_back();
			vv.push_back(node);         //将出队的结点放进数组，因为没有办法直接在pq中判断某一元素是否属于队列，
			//所以当一个元素不在vv中，即在pq中....

			//依次打印每条生成树的边

			if (node.p != NULL)
			{
				cout << "第 " << ++arci << "条边源结点为：" << (node.p)->data
					<< " 目的结点为：" << node.data
					<< " 边的权重为：" << node.key << endl;
			}

			ArcNode *arc = node.firstarc;    //开始遍历node的邻接点
			while (arc != NULL)
			{
				//当node结点的临界结点v不再Qzhong，并且v.key大于边的权重时，
				//更新v的key,并且将v的父结点设为node;整个过程将每个结点的key和p都更新了。
				if (find(vv.begin(), vv.end(), vertices[arc->adjvex]) == vv.end()
					&& arc->weight < vertices[arc->adjvex].key)
				{
					VNode pnode = node;
					vertices[arc->adjvex].p = &pnode;
					vertices[arc->adjvex].key = arc->weight;
				}
				arc = arc->nextarc;
			}
			make_heap(qvnode.begin(), qvnode.end(), PVNodeCompare());
		}
		cout << "*******************************************************" << endl;
	}

protected:
	//初始化邻接链表的表头数组
	void InitVertics()
	{
		cout << "请输入每个顶点的关键字：" << endl;
		VertexType val;
		for (int i = 0; i < vexnum; i++)
		{
			cin >> val;
			vertices[i].data = val;
		}
	}

	//插入一个表结点
	void insertArc(int vHead, int vTail, int weight)
	{
		//构造一个表结点
		ArcNode *newArcNode = new ArcNode;
		newArcNode->source = vHead;
		newArcNode->adjvex = vTail;
		newArcNode->nextarc = NULL;
		newArcNode->weight = weight;

		//arcNode 是vertics[vHead]的邻接表
		ArcNode *arcNode = vertices[vHead].firstarc;
		if (arcNode == NULL)
			vertices[vHead].firstarc = newArcNode;
		else
		{
			while (arcNode->nextarc != NULL)
			{
				arcNode = arcNode->nextarc;		
			}
			arcNode->nextarc = newArcNode;
		}
		arcnum++;
		vertices[vTail].indegree++;         //对弧的尾结点的入度加1
	}

	//依次遍历每个结点的邻接点，遍历每条边，因为无向图，所以每条边相当于在邻接表中出现了两次
	//所以插入时进行一次判断，判断是否已经在边集中，没有则插入，有则放弃
	void initArcs()
	{
		for (int i = 0; i < vexnum; i++)
		{
            ArcNode *node = vertices[i].firstarc;
			
			while (node != NULL)
			{
				ArcLine arc;
                arc.source = i;
				arc.dest = node->adjvex;
				arc.weight = node->weight;
				//判断由邻接表生成的边集是否已经加入数组中，ArcLine要重载==操作，定义什么是相等的边
				if (find_if(arcs.begin(), arcs.end(), bind2nd(equal_to(), arc)) == arcs.end())
				{
					arcs.push_back(arc);
				}
				/*arcs2.insert(arc);*/
				node = node->nextarc;
			}		
		}
		//按照边的权重排序，ArcLine已经重载了<操作符
        sort(arcs.begin(), arcs.end());
	}


	//打印源节点到i的最短路径
	void printPath(int i, int j)
	{
		cout << "从源节点 " << vertices[i].data << " 到目的结点 "
			<< vertices[j].data << " 的最短路径是：" /*<< endl*/;
		__printPath(&vertices[i], &vertices[j]);
		cout << " 权重为：" << vertices[j].key << endl;
	}

	void __printPath(VNode* source, VNode* dest)
	{
		if (source == dest)
			cout << source->data << "->";
		else if (dest->p == NULL)
			cout << " no path！" << endl;
		else
		{
			__printPath(source, dest->p);
			cout << dest->data << "->";
		}
	}

private:
	//const数据成员必须在构造函数里初始化
	static const int MAX_VERTEX_NUM = 20;  //最大顶点个数

	VNode vertices[MAX_VERTEX_NUM];      //存放结点的数组
	vector arcs;      //存放边的数组

	int vexnum;             //图的当前顶点数
	int arcnum;             //图的弧数
};

#endif

/************************************************************
ArraySet.h: 不相交集合的操作
对于这个图，arrayset的DataType为图的结点VertexNode
Date: 2013/12/29
Author: searchop
************************************************************/

#ifndef ARRAYSET_H
#define ARRAYSET_H

#include 
#include 
using namespace std;

template 
struct ArrayNode  
{
	DataType data;
	ArrayNode *p;           //结点的父亲
	int rank;        //结点的高度
	ArrayNode() : p(NULL), rank(0) {}
};

template 
class ArraySet
{
public:
	typedef ArrayNode Node;
	ArraySet(int num) : number(num)
	{

	}

	//使每个结点成为一个单独的集合
	void MakeSet()
	{
		cout << "请输入 " << number << "个数据：" << endl;
		for (int i = 0; i < number; i++)
		{
			DataType val;
			cin >> val;
			Node *nd = new Node;
			nd->p = nd;
			nd->rank = 0;
			nd->data = val;
			vec.push_back(nd);
		}       
	}

	void MakeSet1(DataType &data)
	{
		Node *nd = new Node;
		nd->p = nd;
		nd->rank = 0;
		nd->data = data;
		vec.push_back(nd);           
	}

	Node *getNode(int i)
	{
		return vec[i];
	}

	//带路径压缩的找到x所在的集合
	Node* FindSet(Node *x)
	{
		if (x->p != x)
			x->p = FindSet(x->p);
		return x->p;
	}

	//合并集合，将rank值较小的集合合并到rank值较大的集合
	void UnionSet(Node *nx, Node *ny)
	{
		Node *x = FindSet(nx);
		Node *y = FindSet(ny);
		if (x->rank > y->rank)
			y->p = x; 
		else
		{
			x->p = y;
			if (x->rank == y->rank)   //当两者的rank相同，则使树根的rank增加1
				(y->rank)++;
		}
	}

	void display()
	{
		for (int i = 0; i < number; i++)
		{
			cout << "第 " << i+1 << " 个结点的数据为：" << vec[i]->data 
				<< " 父节点为：" << vec[i]->p->data << " 秩为：" << vec[i]->rank << endl;
		}
		cout << "*************************************************" << endl;
	}

	~ArraySet()
	{
		for (int i = 0; i < number; i++)
		{
			delete vec[i];
			vec[i] = NULL;
		}
	}

private:
	vector vec;
	int number;
};

#endif

#include "ALGraph.h"

int main()
{
	ALGraph wudgGraph(9);
	wudgGraph.CreateWUDG();
	wudgGraph.displayGraph();
	wudgGraph.displayArcs();
	wudgGraph.KRUSKAL();
	wudgGraph.PRIM(1);

	system("pause");
    return 0;
}

运行结果为：