算法导论第24章 单源最短路径

最短路径问题有最优子结构：最短路径的子路径也是最短路径。

如果图中不包含从源节点s可以到达的权重为负值的环路，则对于所有的结点v，最短路径权重有精确定义。

不存在最短路径的两种情况：

1、从结点s到v的某条路径上存在权重为负值的环路，则δ（s,v） = -∞

2、从结点s到v不存在路径，，则δ（s,v） = ∞

最短路径都是简单路径，且不存在环

本章中有三个最短路径算法

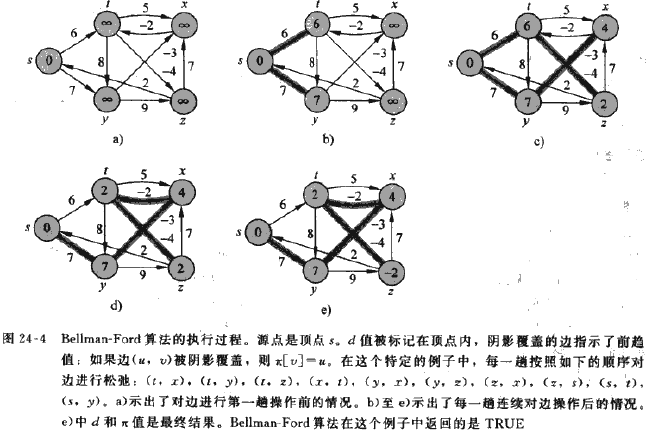
1、Bellman-Ford算法：解决的是一班情况下的单源最短路径问题，可适用于边的权重为负值，且有环路的情况，算法返回一个bool值，表明是否存在一个从源结点可以到达的权重为负值的环路。如果存在，则返回false,否则，可以求出最短路径和这条路径的权重。

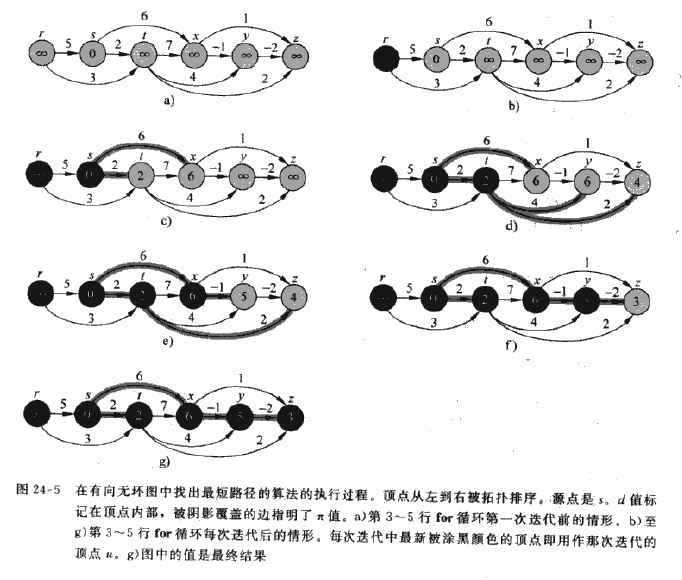
2、Dag_Shortest_Paths: 解决有向无环图的单源最短路径问题，算法根据结点的拓扑排序对带权重的有向无环图G= （V, E）进行边的松弛操作，则可以在θ（V+E）的时间内计算出从单个源节点到所有结点之间的最短路径，允许有负权值的边存在。

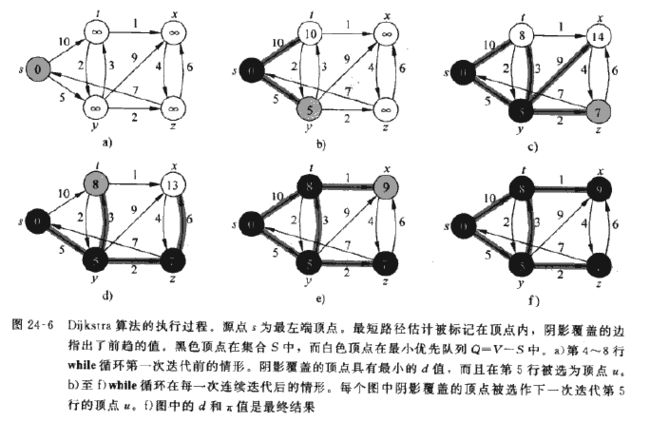
3、Dijkstra算法：解决的是带权重的有向图，算法要去所有的权重大于0，运行时间小于Bellman-Ford算法，算法在运行过程中维持一组结点集合S，从源节点s到该集合中的每个结点之间的最短距离已经找到。算法重复从结点集V-S中选择最短路径估计中最小的结点u，将u加入集合S，然后对从u出发的边进松弛操作。

松弛操作：

在每个结点中维持一个属性v.d ：记录从源节点s到结点v的最短路径权重的上界，称为最短路径估计

首先对最短路径估计和前驱结点进行初始化，即InitializeSingleSource,即将所有结点v.p = NULL, v.d = ∞ ,  然后源点s.d = 0

对每条边（u， v）的松弛操作是：如果源结点s到u的最短路径加上边（u， v）的权重大于s到v的最短路径估计，则对v.d，v.p进行更新，松弛操作可以降低路径的最短路径估计。

三角不等式性质：对于任何边（u， v）属于E，有 δ（s,v）<=  δ(s, u) + w(u, v)

上界性质：对于所有结点有v.d >=  δ（s,v）。一旦v.d的值达到（s,v），则其值不再变化。

BellmanFord算法通过对边进行松弛操作来渐进的降低从源节点s到每个结点v的最短路径估计值v.d，直到最短路径估计与最短路径相同为止。对每条边总共松弛V-1次操作。

求出最短路径后判断是否有负值的环路，判断方法是对每条边（u， v）测试是否v.d > u.d + w(u, v),如果是，则不符合三角不等式性质，则说明存在负环。

运行时间：因为总共有E条边，而每条边都进行V-1次操作，所以时间复杂度为O（V*E）

以下为代码：

//对每个结点的最短路径估计和前驱结点进行初始化，最短路径初始化为INT_MAX, p初始化为NULL
	//并将源节点的key初始化为0
	void InitalizeSingleSource(int index)
	{
		for (int i = 0; i < MAX_VERTEX_NUM; i++)
		{
			vertices[i].key = INT_MAX>>2;
			vertices[i].p = NULL;
		}
		vertices[index].key = 0;
	}

	//对边（u, v）进行松弛，将目前s到v的最短路径v.key与s到u的最短路径加上w(u, v)的值进行比较
	//如果比后面的值还大，则进行更新，将v.key缩短，并且将p置为u
	void relax(ArcNode *arc)
	{
		//竟然溢出了！！
		if (vertices[arc->adjvex].key > vertices[arc->source].key + arc->weight)
		{
			vertices[arc->adjvex].key = vertices[arc->source].key + arc->weight;
			vertices[arc->adjvex].p = &vertices[arc->source];
		}
	}

	//BellmanFord
	bool BellmanFord(int index)
	{
		InitalizeSingleSource(index-1);
		for (int i = 1; i < vexnum; i++)     //循环共进行vexnum-1次
		{
			//遍历所有的边，并对每个边进行一次松弛
			for (int j = 0; j < vexnum; j++)
			{
				for (ArcNode *arc = vertices[j].firstarc; arc != NULL; arc = arc->nextarc)
					relax(arc);
			}
		}
		//再次遍历所有的边，检查图中是否存在权重为负值的环路，如果存在，则返回false
		for (int j = 0; j < vexnum; j++)
		{
			for (ArcNode *arc = vertices[0].firstarc; arc != NULL; arc = arc->nextarc)
			{
				if (vertices[arc->adjvex].key > vertices[arc->source].key + arc->weight)
					return false;
			}
		}
		cout << "BellmanFord求出的单源最短路径：" << endl;
		for (int i = 1; i < vexnum; i++)
		{
			printPath(index-1, i);
		}
		cout << "**************************************************" << endl;
		return true;
	}

代码的运行过程和图如下：

DagShortestPaths算法开始时对图进行拓扑排序，以便获得顶点的先行序列，然后按照这个顺序依次对结点求最短路径：

//用一个栈记录入度为0的结点，当栈不为空时，一个结点出栈，然后依次遍历这个结点
	//的邻接表，对每个邻接的结点的入度减一，邻接的结点入度变为0时进栈，循环直到栈为空
	//用count记录出栈的结点，如果等于vexnum，则图无环，拓扑排序正确，否则，图有环
	pair > TopologicalSort()
	{
		stack stk;
		vector ivec;
		for (int i = 0; i < vexnum; i++)
		{
			if (vertices[i].indegree == 0)
				stk.push(vertices[i]);
		}

		cout << "图的拓扑排序是：" << endl;
		int count = 0;
		while (stk.empty() == false)
		{
			cout << stk.top().data << "->";
			ArcNode *arc = stk.top().firstarc;
			if (arc != NULL)
				ivec.push_back(arc->source);
			stk.pop();			
			count++;
			for (; arc != NULL; arc = arc->nextarc)
			{
				if (!--(vertices[arc->adjvex].indegree))
					stk.push(vertices[arc->adjvex]);
			}
		}
		cout << endl;
		if (count < vexnum)
			return make_pair(false, ivec);
		else
			return make_pair(true, ivec);
	}

	//在有向无环图中，可以按照结点的拓扑顺序来对图的边进行松弛操作，可以带有负的权值
	//按照拓扑排序遍历结点，可以保证边全部被遍历一遍，因为如果有向无环图中有从u到v的一条路径，
	//则u在拓扑排序中的次序位于结点v的前面，
	void DagShortestPaths(int index)
	{
		vector vv = TopologicalSort().second;
		InitalizeSingleSource(index-1);
		for (int i = 0; i < vv.size(); i++)
		{
			ArcNode* arc = vertices[vv[i]].firstarc;
			for (; arc != NULL; arc = arc->nextarc)
				relax(arc);
		}
		cout << "DagShortestPaths求出的单源最短路径：" << endl;
		for (int i = index; i < vexnum; i++)
		{
			printPath(index-1, i);
		}
		cout << "**************************************************" << endl;
	}

算法的时间分析：拓扑排序需要O（V+E）时间，initializeSingleSource需要O（V）时间，for循环对每个顶点只有一次迭代，对每个顶点，其邻接的边依次被relax，即将所有的边遍历了一遍，所以运行时间为要O（V+E）

以下为程序运行图：

Dijkstra算法：权值非负，与Prim类似，与BFS也类似，用到了优先队列，运行时间取决于优先队列的实现方式，

队列的操作有extractmin, insert, decreasekey,代码：

	void Dijkstra(int index)
	{
		InitalizeSingleSource(index-1);
		vector snode;       //保存已经找到最短路径的结点
		vector que;       //保存结点的指针的数组，用这个数组执行堆的算法

		//将结点指针进队列，形成以key为关键值的最小堆
		for (int i = 0; i < vexnum; i++)
			que.push_back(&(vertices[i]));
		//使que按照pvnodecompare准则构成一个最小堆
		make_heap(que.begin(), que.end(), PVNodeCompare());   

		while (que.empty() == false)
		{
			//将队列中拥有最小key的结点出队
			VNode *node = que.front();
			pop_heap(que.begin(), que.end(), PVNodeCompare());   //从堆中删除最小的结点，只是放到了vector的最后
			que.pop_back();      //将vector中的这个结点彻底删除，因为后面还要再排序一次，以免影响后面的堆排序，pop算法。
			snode.push_back(*node);
			for (ArcNode *arc = node->firstarc; arc != NULL; arc = arc->nextarc)
				relax(arc);
			make_heap(que.begin(), que.end(), PVNodeCompare());
		}
		cout << "Dijkstra求出的单源最短路径：" << endl;
		for (int i = 1; i < vexnum; i++)
		{
			if (i != index-1)
			   printPath(index-1, i);
		}
		cout << "**************************************************" << endl;
	}

关于运行时间：extractmin 、insert运行V次，decreasekey运行E次

程序运行情况：

1、队列仅仅用简单数组，每次选择数组中最小的结点extractmin需要O（V），总共出选择V次，所以总共O（V*V），

而insert和decreasekey需要O（1）时间，总共运行E次，所以总运行时间O（V*V+E）

2、用二叉堆实现，则extractmin,decreasekey需要O（lgV）时间，所以运行时间为O（（V+E）lgV）

3、用斐波那契堆实现，运行时间提升到O（VlgV+E），extract-min平摊代价为O（lgV），而decreaseKey平摊时间为O（1）

对于该算法，decreasekey的调用要比extractmin调用一般要多得多，所以不增加extractmin的运行时间，而减小decreasekey的运行时间，都会加快算法的运行时间。

以上为对于本章内容自己的总结~~~