模糊C-means聚类算法和K-means聚类算法
一、模糊C-means聚类算法
1.简介
模糊c-均值聚类算法 fuzzy c-means algorithm (FCMA)或称( FCM)。在众多模糊聚类算法中,模糊C-均值( FCM) 算法应用最广泛且较成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
2. 模糊C-means聚类应用背景
传统的聚类分析是一种硬划分(Crisp Partition),它把每个待辨识的对象严格地划分到某类中,具有“非此即彼”的性质,因此这种类别划分的界限是分明的。然而实际上大多数对象并没有严格的属性,它们在性质和类属方面存在着中介性,具有“亦此亦彼”的性质,因此适合进行软划分。Zadeh提出的模糊集理论为这种软划分提供了有力的分析工具,人们开始用模糊方法来处理聚类问题,并称之为模糊聚类分析。模糊聚类得到了样本属于各个类别的不确定性程度,表达了样本类属的中介性,建立起了样本对于类别的不确定性的描述,能更客观地反映现实世界,从而成为聚类分析研究的主流。
在基于目标函数的聚类算法中模糊C均值(FCM,Fuzzy C—Means)类型算法的理论最为完善,应用最为广泛。
3.模糊C均值聚类的准则
4.模糊C均值算法步骤
(1)设定聚类数目c和加权指数b:
J . C. Bezdek根据经验,认为b 取2 最合适。
Cheung和Chen从汉字识别的应用背景得出b的最佳取值应在1.25~1.75之间。
Bezdek和Hathaway等人从算法收敛性角度着手,得出b 的取值与样本数目n有关的结论,建议b的取值要大于n/(n-2)。
Pal等人从聚类有效性方面的实验研究得到b的最佳选取区间为[1.5, 2.5],在不做特殊要求下可取区间中值b = 2。

用当前的隶属度函数按下式更新计算各类聚类中心:

当模糊C均值算法收敛时,就得到了各类的聚类中心和各个样本对于各类的隶属度值,从而完成了模糊聚类划分。如果需要,还可以将模糊聚类结果进行解模糊,即用一定的规则把模糊聚类划分转化为确定性分类。
5.模糊C均值聚类的MATLAB实现
(一)主要代码
这里对酒瓶颜色进行分类。下面介绍其重要程序代码:
1)MATLAB模糊C均值数据聚类识别函数
在MATLAB中(b=2),只要直接调用如下程序即可实现模糊C均值聚类:
[Center,U,obj_fcn]=fcm(data,cluster_n)
data:要聚类的数据集合,每一行为一个样本;
cluster_n:聚类数;
Center:最终的聚类中心矩阵,每一行为聚类中心的坐标值;
U:最终的模糊分区矩阵;
obj_fcn:在迭代过程中的目标函数值。
注意:在使用上述方法时,要根据中心坐标Center的特点分清楚每一类中心所代表的实际中的哪一类,然后才能准确地将待聚类的各方案准确地分为各自所属的类别;否则,就会出现张冠李戴的现象。
2)MATLAB图形显示聚类模式
使用命令[center,U,obj_fcn] = fcm(data,4)进行聚类后,可调用MATLAB图形窗口显示聚类结果,命令格式如下:
maxU=max(U); %最大隶属度
index1 = find(U(1,:) == maxU) %找到属于第一类的点
index2 = find(U(2,:) == maxU) %找到属于第二类的点
index3 = find(U(3,:) == maxU) %找到属于第三类的点
index4 = find(U(4,:) == maxU) %找到属于第四类的点
为了提高图形的区分度,添加如下命令:
line(data(index1,1),data(index1,2),data(index1,3),'linestyle','none','marker','*','color','g');
line(data(index2,1),data(index2,2),data(index2,3),'linestyle','none','marker','*','color','r');
line(data(index3,1),data(index3,2),data(index3,3),'linestyle','none','marker','+','color','b');
line(data(index4,1),data(index4,2),data(index4,3),'linestyle','none','marker','+','color','y');
(二)全部代码
clear all;
data=[1739.94 1675.15 2395.96
373.3 3087.05 2429.47
1756.77 1652 1514.98
864.45 1647.31 2665.9
222.85 3059.54 2002.33
877.88 2031.66 3071.18
1803.58 1583.12 2163.05
2352.12 2557.04 1411.53
401.3 3259.94 2150.98
363.34 3477.95 2462.86
1571.17 1731.04 1735.33
104.8 3389.83 2421.83
499.85 3305.75 2196.22
2297.28 3340.14 535.62
2092.62 3177.21 584.32
1418.79 1775.89 2772.9
1845.59 1918.81 2226.49
2205.36 3243.74 1202.69
2949.16 3244.44 662.42
1692.62 1867.5 2108.97
1680.67 1575.78 1725.1
2802.88 3017.11 1984.98
172.78 3084.49 2328.65
2063.54 3199.76 1257.21
1449.58 1641.58 3405.12
1651.52 1713.28 1570.38
341.59 3076.62 2438.63
291.02 3095.68 2088.95
237.63 3077.78 2251.96
1702.8 1639.79 2068.74
1877.93 1860.96 1975.3
867.81 2334.68 2535.1
1831.49 1713.11 1604.68
460.69 3274.77 2172.99
2374.98 3346.98 975.31
2271.89 3482.97 946.7
1783.64 1597.99 2261.31
198.83 3250.45 2445.08
1494.63 2072.59 2550.51
1597.03 1921.52 2126.76
1598.93 1921.08 1623.33
1243.13 1814.07 3441.07
2336.31 2640.26 1599.63
354 3300.12 2373.61
2144.47 2501.62 591.51
426.31 3105.29 2057.8
1507.13 1556.89 1954.51
343.07 3271.72 2036.94
2201.94 3196.22 935.53
2232.43 3077.87 1298.87
1580.1 1752.07 2463.04
1962.4 1594.97 1835.95
1495.18 1957.44 3498.02
1125.17 1594.39 2937.73
24.22 3447.31 2145.01
1269.07 1910.72 2701.97
1802.07 1725.81 1966.35
1817.36 1927.4 2328.79
1860.45 1782.88 1875.13];
[center,U,obj_fcn] = fcm(data,4);
plot3(data(:,1),data(:,2),data(:,3),'o');
grid;
maxU=max(U);
index1 = find(U(1,:) == maxU)
index2 = find(U(2,:) == maxU)
index3 = find(U(3,:) == maxU)
index4 = find(U(4,:) == maxU)
line(data(index1,1),data(index1,2),data(index1,3),'linestyle','none','marker','*','color','g');
line(data(index2,1),data(index2,2),data(index2,3),'linestyle','none','marker','*','color','r');
line(data(index3,1),data(index3,2),data(index3,3),'linestyle','none','marker','+','color','b');
line(data(index4,1),data(index4,2),data(index4,3),'linestyle','none','marker','+','color','y');
title('模糊C均值聚类分析图');
xlabel('第一特征坐标');
ylabel('第二特征坐标');
zlabel('第三特征坐标');
6.模糊C均值聚类结果分析
代码结果如下:
>> Untitled
Iteration count = 1, obj . fcn = 29644259.545627
Iteration count = 2, obj. fcn = 22524613.125857
Iteration count = 3, obj. fcn = 20474847.892847
Iteration count = 4, obj. fcn = 15210271.647839
Iteration count = 5, obj. fcn = 11984568.648369
Iteration count = 6, obj. fcn = 11221199.963717
Iteration count = 7, obj. fcn = 10875295.434501
Iteration count = 8, obj. fcn = 10663363.850208
Iteration count = 9, obj. fcn = 10587302.067358
Iteration count = 10, obj. fcn = 10536959.134629
Iteration count = 11, obj. fcn = 10462993.397462
Iteration count = 12, obj. fcn = 10285398.773973
Iteration count = 13, obj. fcn = 9764456.711119
Iteration count = 14, obj. fcn = 8821089.016380
Iteration count = 15, obj. fcn = 8161862.410890
Iteration count = 16, obj. fcn = 7751931.573678
Iteration count = 17, obj. fcn = 7535128.998297
Iteration count = 18, obj. fcn = 7452463.349825
Iteration count = 19, obj. fcn = 7426880.350512
Iteration count = 20, obj. fcn = 7419607.028453
Iteration count = 21, obj. fcn = 7417596.725990
Iteration count = 22, obj. fcn = 7417046.091516
Iteration count = 23, obj. fcn = 7416895.752381
Iteration count = 24, obj. fcn = 7416854.761066
Iteration count = 25, obj. fcn = 7416843.591832
Iteration count = 26, obj. fcn = 7416840.549531
Iteration count = 27, obj. fcn = 7416839.721022
Iteration count = 28, obj. fcn = 7416839.495419
Iteration count = 29, obj. fcn = 7416839.433990
Iteration count = 30, obj. fcn = 7416839.417264
Iteration count = 31, obj. fcn = 7416839.412711
Iteration count = 32, obj. fcn = 7416839.411471
Iteration count = 33, obj. fcn = 7416839.411133
Iteration count = 34, obj. fcn = 7416839.411041
Iteration count = 35, obj. fcn = 7416839.411016
Iteration count = 36, obj. fcn = 7416839.411009
index1 =
8 14 15 18 19 22 24 35 36 43 45 49 50
index2 =
4 6 16 25 32 39 42 53 54 56
index3 =
1 3 7 11 17 20 21 26 30 31 33 37 40 41 47 51 52 57 58 59
index4 =
2 5 9 10 12 13 23 27 28 29 34 38 44 46 48 55
界面如下图:
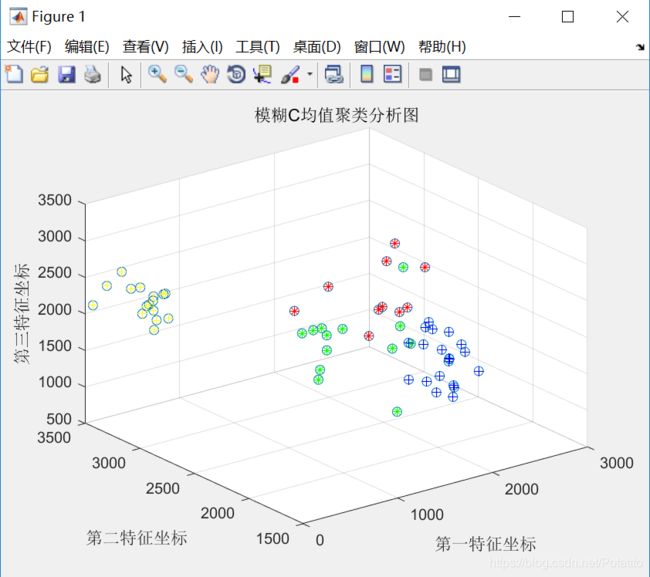
分类结果图如下:
整理出如下表格:
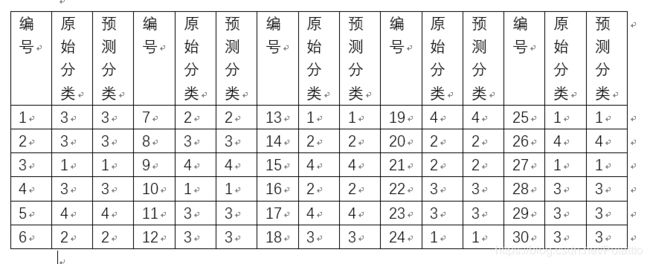
经过对比发现,用模糊C均值进行聚类分析的分类结果与给定结果完全吻合。
二、K-means聚类算法
1.K-means算法的特点
优点:
(1)算法简单、快速。
(2)对处理大数据集,该算法是相对可伸缩的和高效率的。
(3)算法尝试找出使平方误差函数值最小的k个划分。
缺点:
(1)K-means聚类算法只有在簇的平均值被定义的情况下才能使用。
(2)要求用户必须事先给出要生成的簇的数目k。
(3)对初值敏感。
(4)不适合于发现非凸面形状的簇,或者大小差别很大的簇。
(5)对于“噪声”和孤立点数据敏感。
三、模糊C-means聚类算法和K-means聚类算法相比较
通过两个算法的比较得知,C-means算法的结果更优,在实际应用中也被使用的更加广泛。
