LCA三种算法学习(离线算法tarjan+在线算法转rmq+在线倍增)例题poj1330、1470;hdu4547、2874
LCA 问题,即Least Common Ancestors(最近公共祖先)的意思是:给定一有根树,求其两个节点最近的公共祖先;节点的祖先即从节点至根的路径上的节点的集合。
lca离线算法
离线算法,就是要将所有询问先存起来,一起处理,然后再一起输出,与之相对应的是在线算法。在线算法,每给一个询问便可以立即求出答案。
Tarjan算法利用并查集优越的时空复杂度,我们可以实现LCA问题的O(n+Q)算法,这里Q表示询问的次数。Tarjan算法基于深度优先搜索的框架,对于新搜索到的一个结点,首先创建由这个结点构成的集合,再对当前结点的每一个子树进行搜索,每搜索完一棵子树,则可确定子树内的LCA询问都已解决。其他的LCA询问的结果必然在这个子树之外,这时把子树所形成的集合与当前结点的集合合并,并将当前结点设为这个集合的祖先。之后继续搜索下一棵子树,直到当前结点的所有子树搜索完。这时把 当前结点也设为已被检查过的,同时可以处理有关当前结点的LCA询问,如果有一个从当前结点到结点v的询问,且v已被检查过,则由于进行的是深度优先搜索,当前结点与v的最近公共祖先一定还没有被检查,而这个最近公共祖先的包涵v的子树一定已经搜索过了,那么这个最近公共祖先一定是v所在集合的祖先。
首先,Tarjan算法是一种离线算法,也就是说,它要首先读入所有的询问(求一次LCA叫做一次询问),然后并不一定按照原来的顺序处理这些询问。而打乱这个顺序正是这个算法的巧妙之处。看完下文,你便会发现,如果偏要按原来的顺序处理询问,Tarjan算法将无法进行。
Tarjan算法是利用并查集来实现的。它按DFS的顺序遍历整棵树。对于每个结点x,它进行以下几步操作:
* 计算当前结点的层号lv[x],并在并查集中建立仅包含x结点的集合,即root[x]:=x。
* 依次处理与该结点关联的询问。
* 递归处理x的所有孩子。
* root[x]:=root[father[x]](对于根结点来说,它的父结点可以任选一个,反正这是最后一步操作了)。
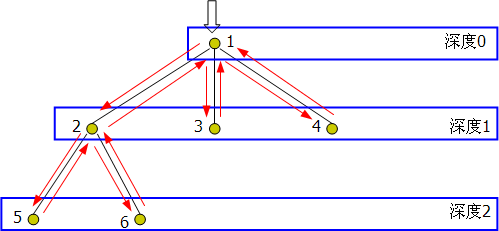
现在我们来观察正在处理与x结点关联的询问时并查集的情况。由于一个结点处理完毕后,它就被归到其父结点所在的集合,所以在已经处理过的结点中(包括 x本身),x结点本身构成了与x的LCA是x的集合,x结点的父结点及以x的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[x]的集合,x结点的父结点的父结点及以x的父结点的所有已处理的兄弟结点为根的子树构成了与x的LCA是father[father[x]]的集合……(上面这几句话如果看着别扭,就分析一下句子成分,也可参照右面的图)假设有一个询问(x,y)(y是已处理的结点),在并查集中查到y所属集合的根是z,那么z 就是x和y的LCA,x到y的路径长度就是lv[x]+lv[y]-lv[z]*2。累加所有经过的路径长度就得到答案。 现在还有一个问题:上面提到的询问(x,y)中,y是已处理过的结点。那么,如果y尚未处理怎么办?其实很简单,只要在询问列表中加入两个询问(x, y)、(y,x),那么就可以保证这两个询问有且仅有一个被处理了(暂时无法处理的那个就pass掉)。而形如(x,x)的询问则根本不必存储。 如果在并查集的实现中使用路径压缩等优化措施,一次查询的复杂度将可以认为是常数级的,整个算法也就是线性的了。
上面内容来自NOCOW
poj1330
先来一道裸题
Nearest Common Ancestors
#include /*有ancr改变join函数的参数顺序无所谓,也就是说ancr其实也可以不用,但此时就必须注意join形参的顺序,在第四个例题hdu2874中采用此法*/
ancr[fnd(son[root][i])]=root;
}
vs[root]=true;//一定要放在循环后面
sz=que[root].size();
for(int i=0;iif(vs[que[root][i]]){
printf("%d\n",ancr[fnd(que[root][i])] );
return ;
}
}
int main(int argc, char const *argv[])
{
int t,head;
cin>>t;
while(t--)
{
scanf("%d",&n);
ms(vs);
ms(ancr);
for(int i=1;i<=n;i++)
pre[i]=i,son[i].clear(),que[i].clear();
for(int i=1;iint fr,sr;
scanf("%d %d",&fr,&sr);
son[fr].push_back(sr);
vs[sr]=true;
}
for(head=1;head<=n;head++) if(!vs[head]) break;
int a,b;
scanf("%d %d",&a,&b);
que[a].push_back(b),que[b].push_back(a);
ms(vs);
LCA(head);
}
return 0;
} poj1470
第二道也可以算是裸题
Closest Common Ancestors
#include true;
sz=qs[nd].size();
for(int i=0;iif(vs[qs[nd][i]])
ans[ancr[fnd(qs[nd][i])]]++;
}
int main(int argc, char const *argv[])
{
int n;
while(scanf("%d",&n)!=EOF)
{
ms(vs);
ms(ancr);
ms(ans);
for(int i=1;i<=n;i++)
{pre[i]=i;node[i].clear(),qs[i].clear();}
for(int i=1;i<=n;i++){
int nd,nm,sr;
scanf("%d:(%d)",&nd,&nm);
while(nm--)
{
scanf("%d",&sr);
node[nd].push_back(sr);
vs[sr]=true;
}
}
int p,a,b;
scanf("%d",&p);
while(p--)
{
while(getchar()!='(') continue;
scanf("%d %d)",&a,&b);
qs[a].push_back(b),qs[b].push_back(a);
}
for(p=1;p<=n;p++) if(!vs[p]) break;
ms(vs);
LCA(p);
for(int i=1;i<=n;i++) if(ans[i])
printf("%d:%lld\n",i,ans[i] );
}
return 0;
} hdu4547
CD操作
#include 1);
join(nd,node[nd][i]);
ancr[fnd(node[nd][i])]=nd;
}
vs[nd]=true;
sz=qs[nd].size();
for(int i=0;iif(vs[qs[nd][i].to]){
ans[qs[nd][i].id]=ancr[fnd(qs[nd][i].to)];
}
}
int main(int argc, char const *argv[])
{
int t;
cin>>t;
while(t--)
{
int n,m,k=0;
scanf("%d %d",&n,&m);
map<string,int > mymap;
ms(vs);
ms(ancr);
ms(ans);
ms(dis);
mymap.clear();
for(int i=1;i<=n;i++)
pre[i]=i,node[i].clear(),qs[i].clear();
for(int i=1;ichar ss1[42],ss2[42];
scanf("%s %s",ss1,ss2);
if(mymap.find(ss1)==mymap.end()) mymap[ss1]=++k;
if(mymap.find(ss2)==mymap.end()) mymap[ss2]=++k;
vs[mymap[ss1]]=true;
node[mymap[ss2]].push_back(mymap[ss1]);
}
for(int i=1;i<=m;i++)
{
char ss1[42],ss2[42];
scanf("%s %s",ss1,ss2);
out[i].frm=mymap[ss1],out[i].to=mymap[ss2];
tmp.to=mymap[ss2],tmp.id=i;
qs[mymap[ss1]].push_back(tmp);
tmp.to=mymap[ss1],tmp.id=i;
qs[mymap[ss2]].push_back(tmp);
}
int head;
for(head=1;head<=n;head++) if(!vs[head]) break;
ms(vs);
LCA(head,0);
for(int i=1;i<=m;i++)
{
if(out[i].frm==out[i].to) printf("0\n");
else if(out[i].frm==ans[i]) printf("1\n");
else if(out[i].to==ans[i])
printf("%d\n",dis[out[i].frm]-dis[ans[i]] );
else printf("%d\n",dis[out[i].frm]-dis[ans[i]]+1 );
}
}
return 0;
} hdu2874
Connections between cities
tarjan的话卡vector, 会MLE, 别图省事用链式前向星做吧。
网上查了一下很多用离线算法做的都mle(上面的原因),本题和标准的LCA模板应用有了不小的区别 ,而且本题没有必要去求出公共祖先,但这道题仍可以帮助更深入理解lca离线算法。
#include LCA在线算法
其实就是将LCA问题转化成RMQ。
1.对有根树T进行DFS,将遍历到的结点按照顺序记下,我们将得到一个长度为2N – 1的序列,称之为T的欧拉序列F。
2.每个结点都在欧拉序列中出现,我们记录结点u在欧拉序列中第一次出现的位置为pos(u)。
3. 根据DFS的性质,对于两结点u、v,从pos(u)遍历到pos(v)的过程中经过LCA(u, v)有且仅有一次,且深度是深度序列B[pos(u)…pos(v)]中最小的,然后就转化成lca啰!
LCA(T, u, v) = RMQ(B, pos(u), pos(v))


poj1330
在线算法
#include for(int i=1;i<=n;i++)
if(i+(1<<(j-1))<=n)
{
int a=dp[i][j-1],b=dp[i+(1<<(j-1))][j-1];
dp[i][j]=(R[a]else dp[i][j]=dp[i][j-1];
}
void query(int a,int b)
{
int k=0;
while((1<<(k+1))<=b-a+1) k++;
int ra=dp[a][k],rb=dp[b-(1<1][k];
if(R[ra]>R[rb]) printf("%d\n",vr[rb] );
else printf("%d\n",vr[ra] );
}
int main(int argc, char const *argv[])
{
int t;
cin>>t;
while(t--)
{
int n;
scanf("%d",&n);
tot=tt=0;
ms(dp);
ms(vs);
msc(head);
for(int i=1;iint a,b;
scanf("%d %d",&a,&b);
vs[b]=true;
addedg(a,b);
addedg(b,a);
}
int a,b;
for(a=1;a<=n;a++) if(!vs[a]) break;
ms(vs);
dfs(a,1);
ST(2*n-1);
scanf("%d %d",&a,&b);
if(frt[a]else query(frt[b],frt[a]);
}
return 0;
} poj1470
在线算法
#include for(int i=1;i<=n;i++)
if(i+(1<<(j-1))<=n){
int a=dp[i][j-1],b=dp[i+(1<<(j-1))][j-1];
dp[i][j]=R[a]else dp[i][j]=dp[i][j-1];
}
void query(int a,int b)
{
int k=0;
while((1<<(k+1))<=b-a+1) k++;
int ra=dp[a][k],rb=dp[b-(1<1][k];
if(R[ra]else ans[vr[rb]]++;
}
int main(int argc, char const *argv[])
{
int n;
while(scanf("%d",&n)!=EOF)
{
ms(vs);
ms(ans);
msc(head);
ms(frt);
ms(dp);
ms(R);
tot=cnt=0;
for(int i=1;i<=n;i++){int np,nm;
scanf("%d:(%d)",&np,&nm);
while(nm--)
{
int sn;
scanf("%d",&sn);
addedg(np,sn);
addedg(sn,np);
vs[sn]=true;
}
}
int head=0;
while(++head<=n) if(!vs[head]) break;
ms(vs);
dfs(head,1);
ST(2*n-1);
int p;
scanf("%d",&p);
while(p--)
{
while(getchar()!='(') continue;
int a,b;
scanf("%d %d)",&a,&b);
if(frt[a]else query(frt[b],frt[a]);
}
for(int i=1;i<=n;i++) if(ans[i])
printf("%d:%d\n",i,ans[i] );
}
return 0;
} LCA在线算法(倍增)
倍增法:
基本思想是:
deep[i] 表示 i节点的深度, fa[i,j]表示 i 的 2^j (即2的j次方) 倍祖先,那么fa[i , 0]即为节点i 的父亲,然后就有一个递推式子:
fa[i,j]= fa [ fa [i,j-1] , j-1 ]
设tmp = fa [i, j - 1] ,tmp2 = fa [tmp, j - 1 ] ,即tmp 是i 的第2 ^ (j - 1) 倍祖先,tmp2 是tmp 的第2 ^ (j - 1) 倍祖先 , 所以tmp2 是i 的第 2 ^ (j - 1) + 2 ^ (j - 1) = 2^ j 倍祖先
这样子一个O(NlogN)的预处理求出每个节点的 2^k 的祖先
然后对于每一个询问的点对a, b的最近公共祖先就是:
先判断是否 d[x]< d[y] ,如果是的话就交换一下(保证 x 的深度大于 y 的深度), 然后把 x 调到与 y 同深度, 同深度以后再把a, b 同时往上调,调到有一个最小的 j 满足fa [x,j] != fa [y,j] (x,y是在不断更新的), 最后再把(x,y)往上调(x=p[x,0], y=p[y,0]) ,一个一个向上调直到x = y, 这时 x或y 就是他们的最近公共祖先。
inline void dfs(int u)
{
int i;
for(i=head[u];i!=-1;i=next[i])
{
if (!deep[to[i]])
{
deep[to[i]] = deep[u]+1;
p[to[i]][0] = u; //p[x][0]保存x的父节点为u;
dfs(to[i]);
}
}
}
void init()
{
int i,j;
//p[i][j]表示i结点的第2^j祖先
for(j=1;(1<< j)<=n;j++)
for(i=1;i<=n;i++)
if(p[i][j-1]!=-1)
p[i][j]=p[p[i][j-1]][j-1];//i的第2^j祖先就是i的第2^(j-1)祖先的第2^(j-1)祖先
}
int lca(int a,int b)//最近公共祖先
{
int i,j;
if(deep[a]<deep[b])swap(a,b);
for(i=0;(1<
i--;
//使a,b两点的深度相同
for(j=i;j> =0;j--)
if(deep[a]-(1<<j)>=deep[b])
a=p[a][j];
if(a==b)return a;
//倍增法,每次向上进深度2^j,找到最近公共祖先的子结点
for(j=i;j>=0;j--)
{
if(p[a][j]!=-1&&p[a][j]!=p[b][j])
{
a=p[a][j];
b=p[b][j];
}
}
return p[a][0];
}