YOLO_v4技巧分解-Cross-Iteration Batch Normalization

对msra的工作都比较关注,最近刚好看到了这篇对传统bn进行改进的论文。
论文地址:https://arxiv.org/abs/2002.05712
github地址:https://github.com/Howal/Cross-iterationBatchNorm
openreview:https://openreview.net/forum?id=BylJUTEKvB
作者应该是投ICLR杯具了,不过个人觉得比较值得少花些时间读一读。
论文开门见山的指出 batchsize的大小直接影响了BN的效果,见图1中的绿色线,batchsize在小于16后的分类准确率急剧下降。作者在本文提出了一种叫做cross-iteration BN的方法,通过泰勒多项式去估计几个连续batch的统计参数,可以很大程度缓解此问题,如图1中的蓝色线,在batchsize逐渐变小时,效果依然稳定,并且accuracy始终高于GN的效果。
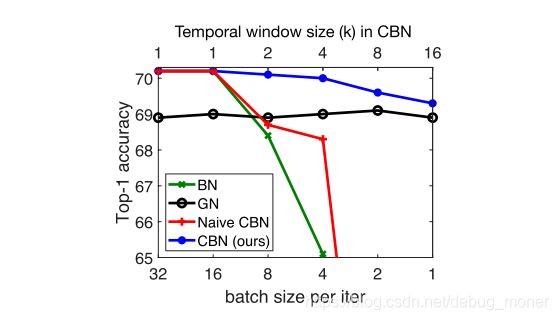
(论文必备图,一图告诉你我有多nb)
1. Revisiting Batch Normalization
从实现的角度来说,BN对特征进行了一种白化操作,可以减少internal covariate shift,具体的可以查看原文。
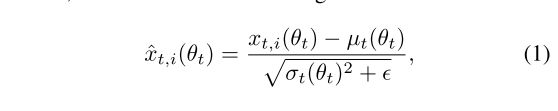
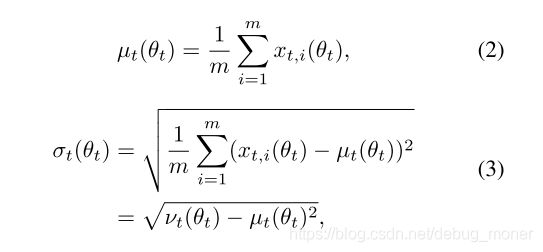
这里作为对比可以回忆下几种比较常见的归一化方法
BatchNormalization,LayerNormization,InstanceNormalization,GroupNormalization
GN的paper中给了一张骨灰级清楚明了的图~
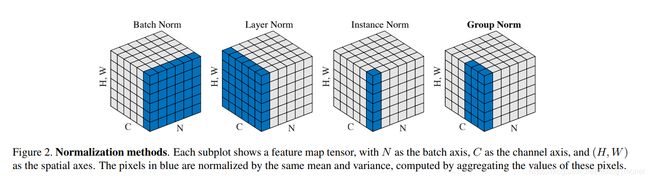
BN的计算中,一个channel就是一个特征N,H,W三个维度进行相关统计参数的计算,pytorch代码如下,其他几种归一化方法只要在BN代码中稍加修改即可。(注意四个参数的维度)
import torch
from torch import nn
class BatchNorm(nn.Module):
'''custom implement batch normalization with autograd by Antinomy
'''
def __init__(self, num_features):
super(BatchNorm, self).__init__()
# auxiliary parameters
self.num_features = num_features
self.eps = 1e-5
self.momentum = 0.1
# hyper paramaters
self.gamma = nn.Parameter(torch.Tensor(self.num_features), requires_grad=True)
self.beta = nn.Parameter(torch.Tensor(self.num_features), requires_grad=True)
# moving_averge
self.moving_mean = torch.zeros(self.num_features)
self.moving_var = torch.ones(self.num_features)
self.reset_parameters()
def reset_parameters(self):
nn.init.uniform_(self.gamma)
nn.init.zeros_(self.beta)
nn.init.ones_(self.moving_var)
nn.init.zeros_(self.moving_mean)
def forward(self, X):
assert len(X.shape) in (2, 4)
if X.device.type != 'cpu':
self.moving_mean = self.moving_mean.cuda()
self.moving_var = self.moving_var.cuda()
Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta,
self.moving_mean, self.moving_var,
self.training, self.eps, self.momentum)
return Y
def batch_norm(X, gamma, beta, moving_mean, moving_var, is_training=True, eps=1e-5, momentum=0.9,):
if len(X.shape) == 2:
mu = torch.mean(X, dim=0)
var = torch.mean((X - mu) ** 2, dim=0)
if is_training:
X_hat = (X - mu) / torch.sqrt(var + eps)
moving_mean = momentum * moving_mean + (1.0 - momentum) * mu
moving_var = momentum * moving_var + (1.0 - momentum) * var
else:
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
out = gamma * X_hat + beta
elif len(X.shape) == 4:
shape_2d = (1, X.shape[1], 1, 1)
mu = torch.mean(X, dim=(0, 2, 3)).view(shape_2d)
var = torch.mean(
(X - mu) ** 2, dim=(0, 2, 3)).view(shape_2d) # biased
X_hat = (X - mu) / torch.sqrt(var + eps)
if is_training:
X_hat = (X - mu) / torch.sqrt(var + eps)
moving_mean = momentum * moving_mean.view(shape_2d) + (1.0 - momentum) * mu
moving_var = momentum * moving_var.view(shape_2d) + (1.0 - momentum) * var
else:
X_hat = (X - moving_mean.view(shape_2d)) / torch.sqrt(moving_var.view(shape_2d) + eps)
out = gamma.view(shape_2d) * X_hat + beta.view(shape_2d)
return out, moving_mean, moving_var
2. Leveraging Statistics from Previous Iterations
既然导致BN效果差的原因是batch太小了,最直白的想法当然是通过扩大用来计算统计信息的样本量解决问题。SyncBN(李沐老师的介绍)就是这个原理,将多张卡上的样本同步计算,一般来讲batchsize大小超过16 后,bn效果基本不会收到影响。这种方法的缺点就是需要不同卡上的数据进行同步以及devices间的数据传递。
本文中的CBN换了一个思路,通过计算几个相近的batch的近似统计参数来解决该问题。
首先作者指出:由于梯度下降机制,模型训练的过程中相近的几个iter所对应的模型参数的变化是平滑的(smoothly)。
假设当前iter index为 t t t,那么 t − τ t-\tau t−τ中的统计量在 t t t时的近似量可以见公式5,6:
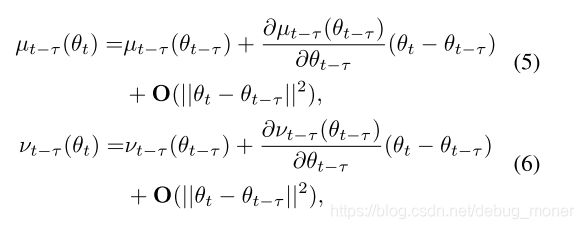
其中 θ \theta θ代表模型的参数, t t t标示计算的是第几个iter,也就是算的batch的idx, μ \mu μ、 ν \nu ν就是BN中的两个统计量。这里其实是 f ( θ t ) f(\theta_t) f(θt)在 θ − θ t − t a u \theta-\theta_{t-tau} θ−θt−tau处泰勒多项式展开,其中** O ( ∣ ∣ θ t − θ t − τ ∣ ∣ 2 ) O(||\theta_t-\theta_{t-\tau}||^2) O(∣∣θt−θt−τ∣∣2)**是 ∣ ∣ θ t − θ t − τ ∣ ∣ ||\theta_t-\theta_{t-\tau}|| ∣∣θt−θt−τ∣∣的二阶无穷小量。在实际的计算时会将高阶无穷小量忽略掉。
在公式5,6中,需要计算 ∂ μ t − τ ( θ t − τ ) ∂ θ t − τ \frac{\partial\mu_{t-\tau}(\theta_{t-\tau})}{\partial\theta_{t-\tau}} ∂θt−τ∂μt−τ(θt−τ)、 ∂ ν t − τ ( θ t − τ ) ∂ θ t − τ \frac{\partial\nu_{t-\tau}(\theta_{t-\tau})}{\partial\theta_{t-\tau}} ∂θt−τ∂νt−τ(θt−τ),加入我们要计算第 l l l层bn的这两个参数,那么在 l l l层之前的所有参数其实都要进行计算,这样子计算量就有些太大了,原文说:
Only when r = l r = l r=l can these gradients be derived in closed form efficiently.
作者在这里又发现:随着layer index r r r 的变小 ( r ≤ l ) (r\leq l) (r≤l), ∂ μ t l ∂ θ t r \frac{\partial\mu_{t}^{l}}{\partial\theta_{t}^{r}} ∂θtr∂μtl、 ∂ ν t l ∂ θ t r \frac{\partial\nu_{t}^{l}}{\partial\theta_{t}^{r}} ∂θtr∂νtl迅速降低,如下图反映了倒数三层的梯度比例:
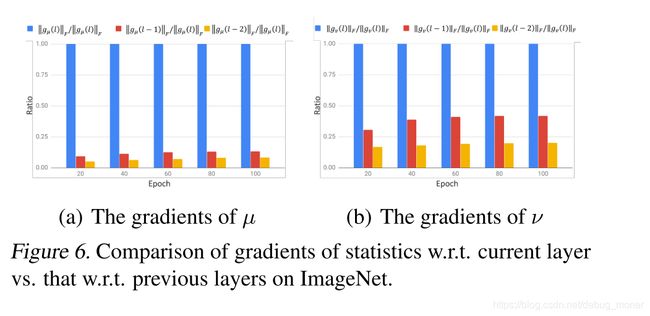 也就是说针对公式5,6我们只要算出统计量对应其所在的层的网络参数的梯度就可以了,这一步简化是非常重要的。
也就是说针对公式5,6我们只要算出统计量对应其所在的层的网络参数的梯度就可以了,这一步简化是非常重要的。
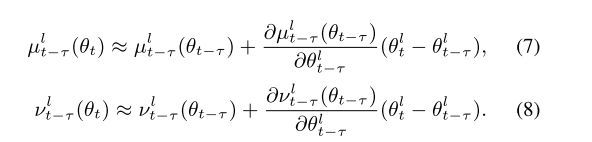
到这里,我们已经计算除了iter t − τ t-\tau t−τ在第 t t t个iter是参数下的统计量近似。论文中给出了一张图
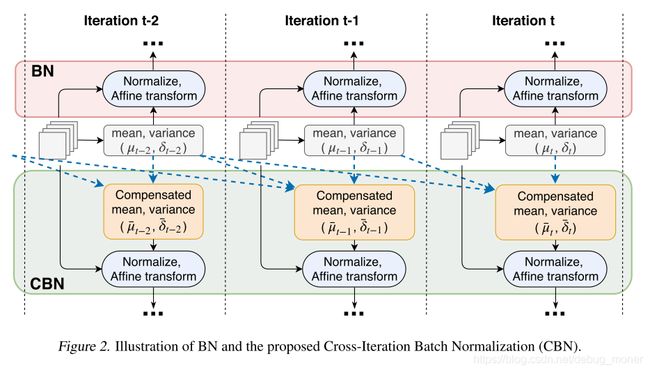
有了上面的近似结果,我们来看一下CBN是如何来进行Normalize的。同上面bn的代码所示,我们怎么去计算CBN相关的统计量,以及执行前向操作。
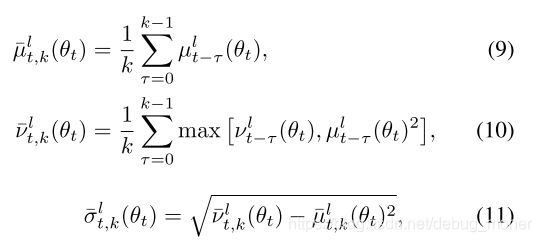
- 对于均值,只需要去计算iter [ t − τ , t ] [t-\tau,t] [t−τ,t]的平均数。
- ν ‾ t , k l ( θ t ) \overline{\nu}_{t,k}^l(\theta_t) νt,kl(θt)定义为 ν t − τ l ( θ t ) \nu_{t-\tau}^l(\theta_t) νt−τl(θt)与 μ t − τ l ( θ ) 2 \mu_{t-\tau}^l(\theta)^2 μt−τl(θ)2中的最大值,再将这个值针对k个iter求平均。文中说这样子才能让 ν ‾ t , k l ( θ t ) \overline{\nu}_{t,k}^l(\theta_t) νt,kl(θt)有意义的统计信息。
现在我们已经有了归一化所需要的所有的统计数据,针对第 l l l层的特征 x t − i l ( θ t ) x_{t-i}^l(\theta_t) xt−il(θt),他的归一化特征为:
x ^ t , i l ( θ t ) = x t , i l ( θ t ) − μ ‾ t , k l ( θ t ) σ ‾ t , k l ( θ t ) 2 + ε \hat{x}_{t,i}^l(\theta_t)=\frac{x_{t,i}^l(\theta_t)-\overline{\mu}_{t,k}^l(\theta_t)}{\sqrt{\overline\sigma_{t,k}^l(\theta_t)^2+\varepsilon}} x^t,il(θt)=σt,kl(θt)2+εxt,il(θt)−μt,kl(θt)
可以看出归一化过程与原始bn算法是一致的。也就是,在做inference过程时,CBN与BN的计算完全相同,所以CBN不增加前向时间
这里值得关注的一个问题,相比于BN,CBN的计算量和memory多用了多少,从上面的分析可以看出,多出来的计算都是在求偏导的那一步,而memory主要是在偏导以及前几个iter的 μ . ν , θ \mu.\nu,\theta μ.ν,θ等几个量的存储与访问。论文指出这些相对于网络本身的计算量与memory占用来比都是微乎其微的。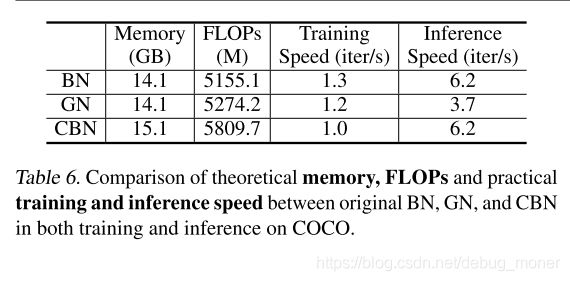
超参数方面,CBN多了一个window size,实验中作者设定为8。并且需要在网络训练初期要用较小的窗大小,随着网络的训练,模型参数也会越来约稳定,这是后再用较大的窗大小可以获得更好的结果。具体细节见论文。
3. Experiment
1. Comparison of feature normalization methods
在imagenet数据bs=32时,对不同的normalize 方式进行对比,可见在大bs的setting下,CBN是唯一一个能够与BN效果一致的归一化方法。

2. Sensitivity to batch size
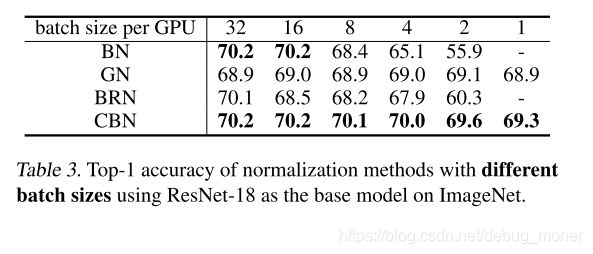
结论:BN与BRN随着bs减小效果下降明显,GN和CBN相对而言在较小的bs下依然可以保持较高的准确率,但CBN的top1 acc 比GN高出0.9%.同时在bs=1时候GN和CBN依然可以进行训练,这是openreview中reviewer比较关心的一个问题,也能看出GN真的还是比较nb的。
- Detection and Segmentation
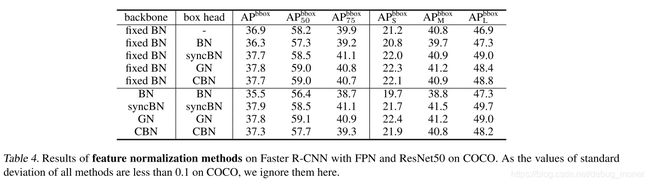
这一部分中作者将backbone和box head 分开进行实验,感觉主要原因是为了方便加载预训练模型,固定backbone的bn不需要在imagenet上重新训练,项目中应用起来会更方便。
- 在固定backbone部分的BN部分时,box head 选择不同的normalize方式,可以看到CBN能够获得与GN,syncBN类似的结果,同时结果要明显好于BN。
- 在backbone和boxhead 都进行normalize的替换后,CBN的结果会明显好于BN但是会比GN和syncBN结果差一些,作者认为是accumulation of approximation error(估计误差累积)造成的。
在论文的最后,作者给出了求两个统计量相对于对应层参数的高效计算方式,大致的思路时计算统计量的第j个维度梯度只跟第j个特征图相关,这里可以省去很大的一部分计算量,完全弄明白后再写这一段。
4. Conclusion
针对BN在small batchsize regime这个问题作者提出了利用相邻iter的样本的方式来提高统计参数的准确性,进而提升模型的效果。针对这个问题LN,IN,GN是通过修改BN中用来计算参数的维度来解决这个问题,同时GN取得了不错的效果;
syncBN是通过将多个GPU上的数据共同利用来扩大batchsize解决该问题。CBN属于利用不同的iter数据来变相扩大batchsize从而改进模型的效果。理论分析清楚明了,实验充分,方法在small batchsize regime这个问题上确实有效。
回过头,我们发现SyncBN效果在各个问题上效果都很好,同时不会引入超参数,不同的深度学习框架也有相应支持。本文相对于SyncBN的优势在哪里?或者是说在什么问题上syncBN不能够使用来突出CBN的必要性。