NOI2018 归程

题目大意

% 　　给出一个 $n$ 个点，$m$ 条边的无向连通图，每条边上有两个参数 $l,a$。其中 $l$ 表示边的长度，$a$ 表示边的海拔（即高度）。对于$Q$个形如 x p 的询问，有如下定义：
　　你有一辆车，可以开着它通过任意海拔严格大于 $p$ 的边，不需要花费任何代价。除此之外，你可以在车开到某个点后，将这辆车彻底报废（这意味着以后都不能再开车），然后通过任意边而不需要考虑其海拔高度，花费为这条边的长度。
　　你需要回答的是从 $x$ 号节点开始，开着一辆车，到达节点1需要的最小代价。强制在线。
　　数据范围　$n\in [0,2\times 10^5]\cap \mathbb{Z},m,q\in [0,4\times 10^5]\cap \mathbb{Z}$
　　　　　　　$l\in [0,2\times 10^5]\cap \mathbb{Z},a\in [0,10^9]\cap \mathbb{Z}$

题解

% 　　什么是kruscal重构树？我们当初在用kruscal求最小生成树的时候，维护连通性用的是并查集，这能十分便捷地判断连通性，但由于路径压缩的缘故，我们完美地丢失了合并的关系，考虑将这种关系建立出来。
　　当我们在执行算法时，考虑边 $⟨(u,v),w⟩$，我们新建一个点 $P$，然后令 $u$ 的祖先和 $v$ 的祖先都认 $P$ 做祖先，然后将边权存在点 $P$ 上作为点 $P$ 的点权。
　　注意这里的做祖先不是在并查集中执行的，而是要真真实实的建出这样的树来，因此需要再新开一个记录父亲的数组，下图是一个已经建好的例子（最大生成树）。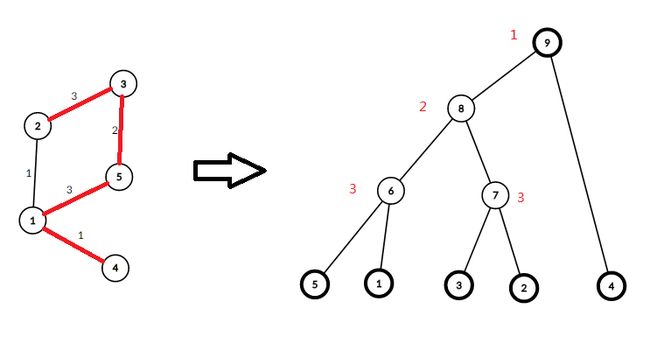
　　其中Kruscal的顺序为(1,5),(2,3),(3,5),(1,4)，即左侧红色线段。
　　按照这种方式来建树，可以发现，点数由原来的 $n$ 个点变为了 $2n-1$ 个，而且上面有很多优秀的性质。如果不看叶子结点，那么这是一个堆，而且点 $u$ 到达点 $v$ 的路径上的边权最大的路径为点 $u$ 和点 $v$ 的最近公共祖先的点权。
　　回到题目中，我们考虑将原图按照海拔建出这样的树，可以发现，对于询问p x，若点 $x$ 的其祖先中，最后一个点权大于 $p$ 的点为 $q$，则说明在以 $q$ 为根的子树内的所有叶子结点均可开车直接到达。
　　由于一个点到根节点的路径上的点的点券单调不上升，因此对于询问 p x，我们用倍增求出点 $q$，然后求出 $q$ 子树中那个点距离点1最近即可。这个过程可以用Dijkstra先预处理出1号点到其它点的距离，然后由叶子结点向上合并答案即可。

代码

% 　　代码经封装，凑合着看。

#include
using namespace std;
#define maxn 200010
#define maxm 400010
struct edge{
	int u,v,w,next;
	bool operator<(const edge &x)const{
		return w>x.w;
	}
};
int CNT=0;
struct Gha{
	edge e[maxm<<1];
	int head[maxn],cnt;
	Gha(){init();}
	void init(){memset(head,cnt=0,sizeof head);}
	void ins(int u,int v,int w){
		e[++cnt]=(edge){u,v,w,head[u]};
		head[u]=cnt;
	}
};
struct dijkstra:public Gha{
	dijkstra(){}
	struct node{
		int u,dis;
		node(int a,int b):u(a),dis(b){}
		bool operator<(const node &x)const{return dis>x.dis;}
	};
	void work(int s,int *f,int n){//预处理最短路
		priority_queue<node> q;
		for(int i=1;i<=n;i++) f[i]=0x3f3f3f3fll;
		f[s]=0; q.push(node(s,0));
		while(!q.empty()){
			node x=q.top(); q.pop();
			int u=x.u;
			if(x.dis!=f[u]) continue;
			for(int i=head[u];i;i=e[i].next){
				int v=e[i].v;
				if(e[i].w+f[u]<f[v]){
					q.push(node(v,f[v]=e[i].w+f[u]));
				}
			}
		}
	}
}_D;
struct kurscal{
	edge e[maxm];
	int f[maxn<<1],cnt;
	kurscal():cnt(0){}
	void init(){cnt=0;}
	void ins(int u,int v,int w){e[++cnt]=(edge){u,v,w};}
	int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
	void work(int);
}_K;
int fa[maxn<<1][21],val[maxn<<1];
void kurscal::work(int n){//重构树的过程
	int cntv=n;//新的点的编号
	for(int i=1;i<=2*n;i++) f[i]=i;
	sort(e+1,e+1+cnt);
	int done=0;
	for(int i=1;i<=cnt&&done<n-1;i++){
		int fx=find(e[i].u),fy=find(e[i].v);
		if(fx!=fy) fa[fx][0]=fa[fy][0]=f[fx]=f[fy]=++cntv,val[cntv]=e[i].w,++done;
	}
}
int dis[maxn<<1];
int n,m;
void prefix(void){
	for(int i=n+1;i<=2*n-1;i++) dis[i]=0x3f3f3f3fll;
	for(int i=1;i<=2*n-1;i++)//预处理子树到1号点的最短距离
		dis[fa[i][0]]=min(dis[fa[i][0]],dis[i]);
	for(int j=1;j<=20;j++)//预处理倍增数组
		for(int i=1;i<=2*n-1;i++)
			fa[i][j]=fa[fa[i][j-1]][j-1];
}
int find(int x,int p){//找x的祖先中最后一个val大于p的节点 
	for(int i=20;i>=0;i--)
		if(fa[x][i]&&val[fa[x][i]]>p) x=fa[x][i];
	return x;
}
inline char nc() {
    static char buf[1000000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline void read(int &sum) {
    char ch=nc();
    int tf=0;
    sum=0;
    while((ch<'0'||ch>'9')&&(ch!='-'))
        ch=nc();
    tf=((ch=='-')&&(ch=nc()));
    while(ch>='0'&&ch<='9')
        sum=sum*10+(ch-48),ch=nc();
    (tf)&&(sum=-sum);
}
int main(void){
	freopen("return.in","r",stdin);
	freopen("return.out","w",stdout);
	int T;read(T);
	while(T--){
		_D.init(); _K.init();//初始化
		read(n);read(m);
		for(int i=1,u,v,l,a;i<=m;i++){
			read(u);read(v);read(l);read(a);
			_D.ins(u,v,l);_D.ins(v,u,l);_K.ins(u,v,a);
		} _D.work(1,dis,n); _K.work(n); prefix();
		int q,k,s; read(q);read(k);read(s);
		for(int i=1,v0,p0,lastans=0;i<=q;i++){
			read(v0);read(p0);
			int v=(v0+k*lastans-1)%n+1;
			int p=(p0+k*lastans)%(s+1);
			printf("%d\n",lastans=dis[find(v,p)]);
		}
	}
	return 0;
}