ICPC Camp 2016 几道神奇的构造打表题
- SJTU Dreadnought Contest
- The Magic Square
- The Kirakira Cycle
- XOR Tree
- Moscow SU Trinity Contest
- Green Day
SJTU Dreadnought Contest
The Magic Square
题意:已知 n≤100 , 你需要用n个边长为整数的正方形凑出一个大正方形,无解输出“Impossible”。
ps:如果加上边长互不相同就成神题了。
考场送分题,几乎全对,关键是怎么实现比较好。
法1:考虑一个正方形,中间划十字多出3个,划九宫格多出8个,然后n大可以凑出来,小数据手推。
#include
#define ForD(i,n) for(int i=n;i;i--)
#define ForkD(i,k,n) for(int i=n;i>=k;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=Pre[x];p;p=Next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=Next[p])
#define Lson (o<<1)
#define Rson ((o<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define vi vector
#define pi pairint ,int> , int> q[10000];
int head=1,tail=1;
void draw2() {
Fork(i,head,tail) {
// printf("%d,%d %d\n",q[i].fi.fi,q[i].fi.se,q[i].se);
}
}
void init() {
q[1]=mp(mp(1,1),1);
}
void work(int X,int Y) {
int p=1;
int x=1;
init();
For(k,Y) {
//draw2();
tian8(l,x);
pairint,int> , int> now=q[head];
Rep(i,3) Rep(j,3) {
if (i||j)
q[++tail] = mp(mp(now.fi.fi +i*p , now.fi.se+j*p ), p );
}
p*=3;
}
kuo2(l);
Fork(i,head,tail) q[i].fi.fi=q[i].fi.fi*2-1,q[i].fi.se=q[i].fi.se*2-1,q[i].se*=2;
// kuo2(l);
// Fork(i,head,tail) q[i].fi.fi=q[i].fi.fi*2-1,q[i].fi.se=q[i].fi.se*2-1,q[i].se*=2;
For(k,X)
{
while (q[head].se<2&&head<=tail) ++head;
if (head>tail) {
tian3(l,x);
q[++tail]=mp(mp(1,l/2+1),l/2);
q[++tail]=mp(mp(l/2+1,1),l/2);
q[++tail]=mp(mp(l/2+1,l/2+1),l/2);
if (++k>X) break;
//draw();
}
plus3(q[head].fi.fi,q[head].fi.se,q[head].se,x); ++head;
}
cout<// draw2();
}
int main() {
l=1; a[1][1]=1; int x=1;
while(cin>>n) {
if (n==2||n==5||n==3) {
puts("Impossible");
return 0;
}
else {
puts("Possible");
int l=16*9;
int x,y;
{
RepD(x,n+1) {
if (n-1-3*x>=0 && (n-1-3*x)%8==0) {
y=(n-1-3*x)/8;
// cout<' '<<x<<' '<<y<x,y);
return 0;
}
}
}
if (n==6) {
cout<<"3"<"1 1 2");
puts("1 1 3");
puts("6 5 4");
return 0;
}
if (n==8) {
puts("4");
puts("1 1 1 2");
puts("1 1 1 8");
puts("1 1 1 7");
puts("3 4 5 6");
return 0;
}
if (n==11) {
puts("8");
puts("1 1 1 2 2 2 3 3");
puts("1 1 1 2 2 2 3 3");
puts("1 1 1 2 2 2 6 6");
puts("4 4 4 5 5 5 6 6");
puts("4 4 4 5 5 5 7 7");
puts("4 4 4 5 5 5 7 7");
puts("8 8 9 9 10 10 11 11");
puts("8 8 9 9 10 10 11 11");
return 0;
}
if (n==14) {
puts("9");
puts("1 1 2 2 3 3 10 10 10");
puts("1 1 2 2 3 3 10 10 10");
puts("4 4 5 5 6 6 10 10 10");
puts("4 4 5 5 6 6 11 11 11");
puts("7 7 8 8 9 9 11 11 11");
puts("7 7 8 8 9 9 11 11 11");
puts("12 12 12 13 13 13 14 14 14");
puts("12 12 12 13 13 13 14 14 14");
puts("12 12 12 13 13 13 14 14 14");
return 0;
}
if (n==17) {
puts("14");
puts("1 1 1 1 1 1 2 2 2 2 2 2 5 5");
puts("1 1 1 1 1 1 2 2 2 2 2 2 5 5");
puts("1 1 1 1 1 1 2 2 2 2 2 2 7 7");
puts("1 1 1 1 1 1 2 2 2 2 2 2 7 7");
puts("1 1 1 1 1 1 2 2 2 2 2 2 9 9");
puts("1 1 1 1 1 1 2 2 2 2 2 2 9 9");
puts("3 3 3 3 3 3 4 4 4 4 4 4 11 11");
puts("3 3 3 3 3 3 4 4 4 4 4 4 11 11");
puts("3 3 3 3 3 3 4 4 4 4 4 4 13 13");
puts("3 3 3 3 3 3 4 4 4 4 4 4 13 13");
puts("3 3 3 3 3 3 4 4 4 4 4 4 15 15");
puts("3 3 3 3 3 3 4 4 4 4 4 4 15 15");
puts("6 6 8 8 10 10 12 12 14 14 16 16 17 17");
puts("6 6 8 8 10 10 12 12 14 14 16 16 17 17");
return 0;
}
}
}
return 0;
} 刚才那个做法太麻烦了,我们考虑3个初始状态,分别是
1,6(九宫格其中4个合并成1个),8(16宫格9个合并成一个),然后不停划十字,小数据手推
受6和8的影响,我们考虑2个正方形对角抵在一起,剩下全用1*1填的情况
这题可以胡乱构造出来真心。
The Kirakira Cycle
题意:已知 fn(x)=∑ni=1(xmodi) ,构成了一个x到 fn(x) 的映射,这定义了一张图,对于每个点x只有一条有向边从该点出发,指向 fn(x) ,那么请问图中最大环的长度,只有 n≤104 是已知的。
毫无规律,只好打表,问题是怎么打。
显然 fn(x)−fn(x−1)=n−∑d<=nd|xd
而且最长环出现的数主要在 [3/20(1+2+...+n),3/10(1+2+...+n)]
于是根据这个对于n太大的情况打表,小数据暴力。
还有随机的作法:因为链很长,所以在那个区间找10个点当起点试试就行了。(没试过)
XOR Tree
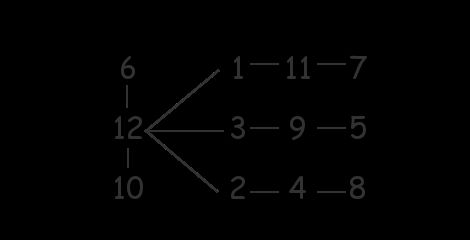
一棵树n个节点,编号1..n,构造一颗树,使至少n+1对节点满足路径上节点编号的xor和为零。
Moscow SU Trinity Contest
Green Day
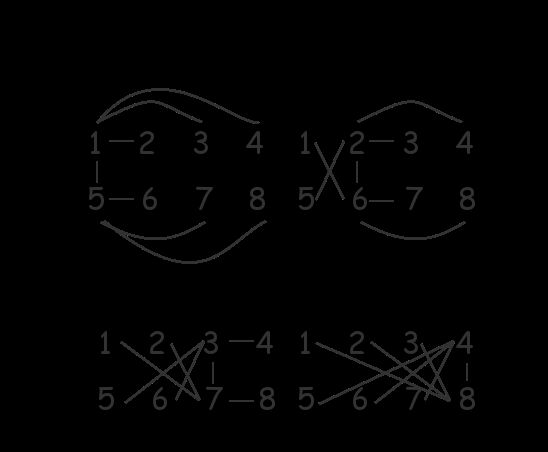
题意:给定 k≤100 ,求k个树,这些树节点数相同,且任意2图不出现下列情况:
存在两点(u,v),两棵树中路径(u,v)都经过不为u,v的点c
求任意解
#include
#define ForD(i,n) for(int i=n;i;i--)
#define ForkD(i,k,n) for(int i=n;i>=k;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=Pre[x];p;p=Next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=Next[p])
#define Lson (o<<1)
#define Rson ((o<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (500000000000LL)
#define F (100000007)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define vi vector
#define pi pair1 ,k) cout<' '<' '<< j+k <1,i-1) cout<' '<' '<cout<' '<return 0;
}