1
其实四百年来,相对于中国古老的、朴素的科技成果,西方这四百年的科技成果炫目的很多很多,如满天繁星,难以胜数。但哥哥只挑选了水泥和塑料来说事,一则是这两样东西在我们生活中应用极为广泛,可以说是如影随形,无处不在。二则通过这两则故事,可以看到东西方的一些差异。
工业革命前,海盗和渔民通过粘合剂(早期的水泥)修建灯塔,工业革命带动的巨大需求,导致水泥有了更广泛的应用,而应用中更高的质量要求又进一步推动了技术的创新。
就这样,在发明、改进、创新和不断扩大应用之间,科技进入了快速发展时期,正如一场完全停不下来的接力赛如火如荼。工匠、技师、工人、学者、科学家、爱好者发烧友……都主动或被动卷入这样一场前所未有的洪流中,迅速改变着人类的生存状态。
在东方,是传男不传女,传嫡不传庶,传长不传幼。在西方,则通过专利制度解决权益切分。最早实行专利制度的是威尼斯,它在1474年颁布了第一部具有近代特征的专利法。以后,专利制度在世界各国得到了广泛的应用。为了促进国际交流合作和技术贸易,各国先后签订了一些有关保护工业产权的国际公约。
1883年,在巴黎由法国等11个国家缔结的《保护工业产权巴黎公约》是第一个也是至今为止最重要的国际专利公约,截至1984年已有94个国家参加。1980年,中国成立了专利局;1984年颁布了《中华人民共和国专利法》;1985年加入了《保护工业产权巴黎公约》。从1474年到1980年是整整五百年的历史。而观念上的转变却还不仅仅一本法律就可体现。
2
两个故事里,贯穿始终的科学精神才弥足珍贵。
何谓科学精神?教条千万条,实不如故事简明之万一。
1687年牛顿在《自然哲学的数学原理》一书中提出了万有引力定律和运动三定律。牛顿根据万有引力理论推断:地球应该是个在赤道处鼓起而在两极扁平的扁球体。另一位科学家卡西尼则依据地球绕日运动的影响推断地球是个两极拉长的扁长球体。
到底地球真正的形状是什么样子的呢?
18世纪30年代,法国科学院派出了两个远征队,一队到北极圈附近的拉普兰,一队到赤道附近的秘鲁,分别测量两地子午线的长度。历经十几年的精细勘测,最终证明牛顿的预测是正确的,而卡西尼的假设是错误的。
科学精神的力量让人们能够拥有批判的头脑,能够进行理性的思考,能够展开自由的讨论,能够接受实践的检验。
科学精神让人们尊重事实,尊重真理,反对迷信,反对盲从,反对因循守旧。
3
说到科学精神,最后讲一则牛顿这位天才的精彩八卦:牛顿、约翰?伯努利与最速降线的故事。
首先简单解释一下什么是最速降线问题:想象一个小球沿着一条曲线在重力作用下,由A点下降至B点(B点不在A点垂直下方),问沿着怎样的曲线下降所需的时间最短。
看不明白也没关系,这问题本身并不重要。
瑞士数学家约翰-伯努利(下文称伯努利)经过潜心研究,解出了这个问题的答案。得意洋洋的伯努利在1696年6月向全欧洲的数学家发出挑战,并说道:“如果在年底之前还没有人能够解决这个难题,我将在1697年1月1日公布答案。”
尽管众多的欧洲数学家们都被这个挑战所吸引,并投身于该问题的求解中,可到了截止日期时,伯努利只收到了他的老师莱布尼茨寄来的一份答案。为了让欧洲的数学家们有足够的时间求解这一精彩的难题,伯努利将截止日期推迟到了1967年的复活节。
现在伯努利更加嚣张了,公开宣称解开这个问题的人将得到最高的荣誉和赞美(当然,他自己早就解出了答案)。为了向他最不服气的牛顿炫耀自己的才智,伯努利甚至将这个问题抄了一遍,直接寄给牛顿本人。此时的牛顿已经54岁了,头脑已经远远不如全盛时期那样的机敏。收到问题的当天,牛顿正在造币局忙着改铸新币的事情。当筋疲力尽的牛顿晚上回到家中看到伯努利的信后,顿时感觉不爽,花了几个小时就解出了这个问题。牛顿甚至都不屑于在上面署名就把答案寄回给了伯努利。
1697年复活节的挑战截止日期到来的时候,伯努利一共收到了四份答案。他的老师莱布尼茨、他的哥哥雅各布-伯努利、洛比达侯爵各提供了一份答案。第四份答案没有署名,但是却完全正确。从信封上的英国邮戳来看,这份答案的主人非伊萨克-牛顿爵士莫属。伯努利看着信封上的邮戳,怀着敬畏之心说道:“我从他的利爪认出了这头狮子”。
4
数学世家伯努利家族
也许这样看,大家还看不到这个故事特别值得玩味的地方,那么哥哥再延伸一点料给兄弟们看看。
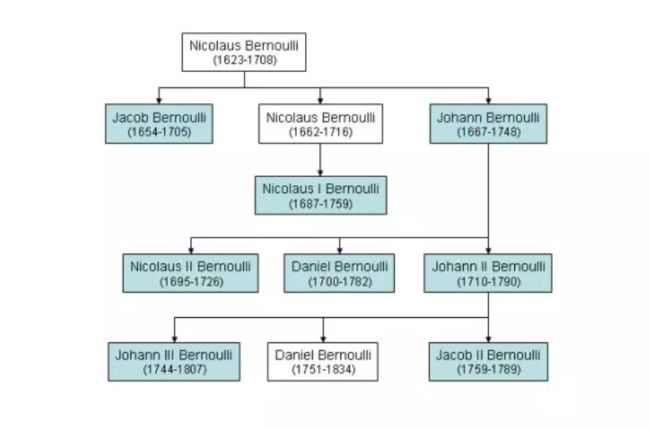
伯努利家族,又译贝努利家族。17-18世纪瑞士巴塞尔的数学和自然科学家的大家族,祖孙三代,出过十多位数学家原籍比利时安特卫普,1583年遭受天主教迫害,迁往德国法兰克福,最后定居巴塞尔,主要成员的世系如下:
最重要的是雅各布第一·伯努利、约翰第一·伯努利和丹尼尔第一·伯努利。
雅各布第一·伯努利1654年12月27日生于瑞士巴塞尔,1705年8月16日卒于同地。最初遵从父亲的意见学神学,当他读了R.笛卡尔、J.沃利斯的书后,颇受启发,兴趣转向数学。
1676年到荷兰、英国等处,结识当地学者、从1687年起直到去世,任巴塞尔大学教授。他和弟弟约翰第一·伯努利是G.W.莱布尼茨的朋友,他们迅速掌握了莱布尼茨的微积分并加以发扬光大。
雅各布在《学艺》上发表一系列的论文,1694年他首次给出直角坐标和极坐标下的曲率半径公式,这也是系统地使用极坐标的开始1690年他提出悬链线问题,后来又改变条件,解决了更复杂的悬链问题。1694年的论文讨论了双纽线的性质,伯努利双纽线因此得名。1695年他提出著名的伯努利方程。
雅各布对对数螺线深有研究,他发现对数螺线经过各种变换后,结果还是对数螺线。在惊叹这曲线的奇妙之余,遗言要将这曲线刻在墓碑上,并附以颂词:“纵使变化,依然故我”。雅各布的巨著《猜度术》(1713)的出版,是组合数学及概率论史的一件大事,书中给出的伯努利数有很多应用。还有伯努利定理,这是大数定理的最早形式。
约翰第一·伯努利1667年8月6日生于巴塞尔,1748年1月1日卒于同地。最初学医,同时研习数学。1691年到巴黎,曾为洛必达的私人教师。现今求不定式极限的洛必达法则,实出自约翰。
1705年接替其巴雅各布任巴塞尔大学教授。1691年解出悬链线问题1696年,他向全欧洲数学家挑战,提出最速降曲线问题:“一质点受地心引力的作用,自较高点下滑至较低点,不计磨擦,问沿着什么曲线,时间最短?”
问题的难度处于和普通的极大极小值求法不同,它是要求出一个未知函数(曲线)来满足所给条件。洛必达、莱布尼茨、I·牛顿、雅各布第一·伯努利都给出这个问题的解答,后来引起变分法的产生。
尼古拉第二·伯努利,约翰第一·伯努利的儿子,13岁入巴塞尔大学,1715年取得法学硕士学位。1725年同其弟弟丹尼尔第一·伯努利一起应邀到彼得堡去。他到彼得堡后。曾提出一个概率论问题,后来以彼得堡问题著称,
可惜次年就死在那里。
丹尼尔第一·伯努利,1700年2月8日生于荷兰格罗宁根,1782年3月17日卒于巴塞尔丹。尼尔25岁就成为彼得堡科学院数学教授,他最早的论著是解决黎卡提方程(1724)。他在概率论、偏微分方程、物理等方面均有贡献。曾获法国科学院奖金10次之多。他的《流体动力学》1738年出版,这是作为流体动力学基础的“伯努利定理”的出处。1733年他回到巴塞尔,教授解剖学、植物学和自然哲学。
OK,一切讲完,试问各位兄弟:这样背景下,牛顿与伯努利的故事在东方会怎样演绎?你懂的。