【NCPC2017-2018-gym101572-A.Airport Coffee 】 线段树+分类讨论DP
Airport Coffee
题目链接：
https://codeforces.com/gym/101572/problem/A
Description
Input
Output
Sample Input
100000 100 138 60 300
5
5000 20000 50000 55000 75000
Sample Output
2
0 3
题意
从 0 0 0这个位置出发走到 l l l这个位置，速度为 a a a，路上有 n n n个咖啡店，可以选择在某个咖啡店买或者不买咖啡，如果选择买咖啡，需要用 t t t的时间等咖啡变凉，在这 t t t的时间内速度为 a a a,之后可以喝咖啡走 r r r时间的路，在这期间速度为 b b b。拥有咖啡的同时仍然可以买咖啡。问走到 l l l这个位置的最短时间。
题解
首先这道题要考虑倒着做，因为最后一个咖啡店选择喝/不喝咖啡到达l的时间是确定的，我们只要倒着推就可以。
之后我们考虑从i这个点到达终点的最优值一定可以从某个j咖啡店转移过来，我们怎么保证最优的。
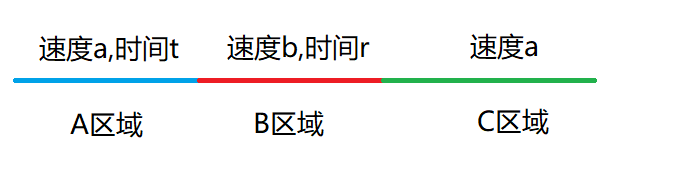
首先分析一下在i这个点喝咖啡之后，一共有以下三个区域。
首先通过二分找出所有在每个区域中的最左咖啡店和最右咖啡店。
设当前点的位置为 p o s [ i ] pos[i] pos[i],选择的咖啡店的位置为 p o s [ j ] pos[j] pos[j]
设 d p [ i ] dp[i] dp[i]为从i咖啡店走到终点的最短时间。
分析C区域
d p [ i ] = ( d i s [ j ] − d i s [ i ] − a ∗ t − b ∗ r a + d p [ j ] + t + r ) dp[i] = (\frac{dis[j]-dis[i]-a*t-b*r}{a}+dp[j]+t+r) dp[i]=(adis[j]−dis[i]−a∗t−b∗r+dp[j]+t+r)
我们发现dp[i]只和 d i s [ j ] a + d p [ j ] \frac{dis[j]}{a}+dp[j] adis[j]+dp[j]有关，其他都是常量，所以我们只要用一棵线段树存储这个信息即可。
分析B区域
d p [ i ] = ( d i s [ j ] − d i s [ i ] − a ∗ t b + t + d p [ j ] ) dp[i]=(\frac{dis[j]-dis[i]-a*t}{b}+t+dp[j]) dp[i]=(bdis[j]−dis[i]−a∗t+t+dp[j])
我们发现dp[j]只和 d i s [ j ] b + d p [ j ] \frac{dis[j]}{b}+dp[j] bdis[j]+dp[j]有关，其他都是常量，所以我们只要用一棵线段树存储这个信息即可。
分析A区域
d p [ i ] = ( d i s [ j ] − d i s [ i ] ] a + d p [ j ] ) dp[i]=(\frac{dis[j]-dis[i]]}{a}+dp[j]) dp[i]=(adis[j]−dis[i]]+dp[j])
我们发现dp[i]只和 d i s [ j ] a + d p [ j ] \frac{dis[j]}{a}+dp[j] adis[j]+dp[j]有关，其他都是常量，而这个在分析C区域中的线段树已经维护，不需要再维护。
之后就倒着DP用线段树转移即可，转移的时候要注意可以转移的咖啡店的范围，要注意边界条件以及最初的pos就是爆int的。
代码
#include
#define dbg(x) cout<<#x<<" = "<
#define dbg2(x1,x2) cout<<#x1<<" = "<#define dbg3(x1,x2,x3) /*cout<<#x1<<" = "<#define print(a,n) for(int i=1;i<=n;i++) cout<
#define pb push_back
#define Fi first
#define Se second
#define ll long long
#define ull unsigned long long
#define pii pair