【2019 江苏省队集训】Day2 解题报告

【T1】 朝夕相处

【思路要点】

• 记不考虑旋转同构的答案为 $G(N)$，答案为$F(N)$，由$Burnside$引理，有$$F(N)=\frac{{\sum }_{i\mid N}G(i)\phi (\frac{N}{i})}{N}$$
• 剩余问题在于计算 $G(N)$ ，考虑状态 $(i,Cola,Colb,Dista,Distb)$ ，表示完成左端点在 $i$ 之前的所有瓷砖的放置与染色后，第一行最后一个瓷砖颜色为 $Cola$ ，位置为 $i+Dista$ ，第二行最后一个瓷砖颜色为 $Colb$ ，位置为 $i+Distb$ 。枚举左端点在 $0$ 处时的状态，计算转移到 $N$ 处的相同状态的方案数，对于所有状态求和，即为 $G(N)$ 。
• 使用矩阵乘法或 $Berlekamp-Massey$ 算法可以对该动态规划进行优化。
• 状态总数为 $O(K^2)$，若采用 $Berlekamp-Massey$ 算法优化动态规划，总时间复杂度为 $O(M{K}^{6}LogK+M^2\sqrt{N}LogN)$ ，其中 $M$ 为递推阶数，有 $M=31$ 。
• 用最小表示法表示一个状态的颜色可将状态总数降至$O(M)$，总时间复杂度降为 $O(M^{4}LogM+M^2\sqrt{N}LogN)$

【代码】

#include
using namespace std;
const int MAXN = 105;
const int P = 1e9 + 7;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
int power(int x, int y) {
	if (y == 0) return 1;
	int tmp = power(x, y / 2);
	if (y % 2 == 0) return 1ll * tmp * tmp % P;
	else return 1ll * tmp * tmp % P * x % P;
}
void update(int &x, int y) {
	x += y;
	if (x >= P) x -= P;
}
namespace LinearSequence {
	const int MAXN = 5005;
	const int MAXLOG = 62;
	const int P = 1e9 + 7;
	vector <int> a[MAXN];
	int cnt, delta[MAXN], fail[MAXN];
	int k, h[MAXN], now[MAXLOG][MAXN];
	int power(int x, int y) {
		if (y == 0) return 1;
		int tmp = power(x, y / 2);
		if (y % 2 == 0) return 1ll * tmp * tmp % P;
		else return 1ll * tmp * tmp % P * x % P;
	}
	void times(int *res, int *x, int *y) {
		static int tmp[MAXN];
		memset(tmp, 0, sizeof(tmp));
		for (int i = 0; i <= k - 1; i++)
		for (int j = 0; j <= k - 1; j++)
			tmp[i + j] = (tmp[i + j] + 1ll * x[i] * y[j]) % P;
		for (int i = 2 * k - 2; i >= k; i--) {
			int val = tmp[i]; tmp[i] = 0;
			for (unsigned j = 0; j < a[cnt].size(); j++)
				tmp[i - j - 1] = (tmp[i - j - 1] + 1ll * val * a[cnt][j]) % P;
		}
		memcpy(res, tmp, sizeof(tmp));
	}
	void init(int n, int *val) {
		for (int i = 0; i <= cnt; i++)
			a[i].clear();
		cnt = 0;
		for (int i = 1; i <= n; i++) {
			delta[i] = val[i];
			for (unsigned j = 0; j < a[cnt].size(); j++)
				delta[i] = (delta[i] - 1ll * a[cnt][j] * val[i - j - 1] % P + P) % P;
			if (delta[i] == 0) continue;
			fail[cnt] = i;
			if (cnt == 0) {
				a[++cnt].resize(i);
				continue;
			}
			int mul = 1ll * delta[i] * power(delta[fail[cnt - 1]], P - 2) % P;
			a[cnt + 1].resize(i - fail[cnt - 1] - 1);
			a[cnt + 1].push_back(mul);
			for (unsigned j = 0; j < a[cnt - 1].size(); j++)
				a[cnt + 1].push_back(1ll * a[cnt - 1][j] * (P - mul) % P);
			if (a[cnt + 1].size() < a[cnt].size()) a[cnt + 1].resize(a[cnt].size());
			for (unsigned j = 0; j < a[cnt].size(); j++)
				a[cnt + 1][j] = (a[cnt + 1][j] + a[cnt][j]) % P;
			cnt++;
		}
		assert(n >= a[cnt].size() * 2 + 5);
		memset(now, 0, sizeof(now));
		k = a[cnt].size();
		if (k == 1) now[0][0] = a[cnt][0];
		else now[0][1] = 1;
		for (int i = 1; i <= 2 * k; i++)
			h[i] = val[i];
		for (int p = 1; p < MAXLOG; p++)
			times(now[p], now[p - 1], now[p - 1]);
	}
	int query(long long n) {
		if (n <= k) return h[n]; n -= k;
		static int res[MAXN];
		memset(res, 0, sizeof(res));
		res[0] = 1;
		for (int p = 0; p < MAXLOG; p++) {
			long long tmp = 1ll << p;
			if (n & tmp) times(res, res, now[p]);
		}
		int ans = 0;
		for (int i = 0; i <= k - 1; i++)
			ans = (ans + 1ll * res[i] * h[i + k]) % P;
		return ans;
	}
}
struct State {int cola, colb, dista, distb; };
bool operator < (State a, State b) {
	if (a.cola == b.cola) {
		if (a.colb == b.colb) {
			if (a.dista == b.dista) return a.distb < b.distb;
			else return a.dista < b.dista;
		} return a.colb < b.colb;
	} return a.cola < b.cola;
}
int n, m, ans[MAXN];
set <pair <State, int>> start;
map <State, int> mp[MAXN];
void initstates() {
	State now = (State) {0, 0, 0, 0}, res = now;
	res.cola = res.colb = 1;
	start.emplace(res, m);
	for (int dj = 1; dj <= 3; dj++)
	for (int dk = 1; dk <= 3; dk++) {
		State res = now;
		res.dista = dj, res.distb = dk;
		res.cola = 1, res.colb = 2;
		res.dista--, res.distb--;
		start.emplace(res, 1ll * m * (m - 1) % P);
	}
}
int phi(int x) {
	int ans = x;
	for (int i = 2; i * i <= x; i++)
		if (x % i == 0) {
			ans = ans / i * (i - 1);
			while (x % i == 0) x /= i;
		}
	if (x != 1) ans = ans / x * (x - 1);
	return ans;
}
int main() {
	freopen("experience.in", "r", stdin);
	freopen("experience.out", "w", stdout);
	int num, N;
	read(num), read(N);
	n = 70, m; read(m);
	initstates();
	for (auto s : start) {
		for (int i = 0; i <= n; i++)
			mp[i].clear();
		mp[0][s.first] = 1;
		for (int i = 1; i <= n; i++)
		for (auto x : mp[i - 1]) {
			State now = x.first;
			if (now.dista == 0 && now.distb == 0) {
				for (int j = 1; j <= m && j <= 5; j++)
					if (j == 5) {
						State res = now;
						res.dista = res.distb = 0;
						res.cola = res.colb = 4;
						update(mp[i][res], 1ll * x.second * (m - 4) % P);
					} else if (j != now.cola && j != now.colb) {
						State res = now;
						res.dista = res.distb = 0;
						res.cola = res.colb = j;
						update(mp[i][res], x.second);
					}
				if (now.cola == now.colb) {
					for (int j = 1; j <= m && j <= 5; j++)
					for (int dj = 1; dj <= 3; dj++)
					for (int k = 1; k <= m && k <= 5; k++)
					for (int dk = 1; dk <= 3; dk++)
						if (j == 5 && k == 5) {
							State res = now;
							res.dista = dj, res.distb = dk;
							res.cola = 3, res.colb = 4;
							res.dista--, res.distb--;
							update(mp[i][res], 1ll * x.second * (m - 4) % P * (m - 5) % P);
						} else if (j == 5) {
							if (k != now.colb) {
								State res = now;
								res.dista = dj, res.distb = dk;
								res.cola = 4, res.colb = k;
								if (k == 4) res.cola = 3;
								res.dista--, res.distb--;
								update(mp[i][res], 1ll * x.second * (m - 4) % P);
							}
						} else if (k == 5) {
							if (j != now.cola) {
								State res = now;
								res.dista = dj, res.distb = dk;
								res.cola = j, res.colb = 4;
								if (j == 4) res.colb = 3;
								res.dista--, res.distb--;
								update(mp[i][res], 1ll * x.second * (m - 4) % P);
							}
						} else if (j != now.cola && k != now.colb && j != k) {
							State res = now;
							res.dista = dj, res.distb = dk;
							res.cola = j, res.colb = k;
							res.dista--, res.distb--;
							update(mp[i][res], x.second);
						}
				}
			} else if (now.dista == 0) {
				for (int j = 1; j <= m && j <= 5; j++)
				for (int dj = 1; dj <= 3; dj++)
					if (j == 5) {
						State res = now;
						res.dista = dj, res.cola = 4;
						if (res.colb == 4) res.cola = 3;
						res.dista--, res.distb--;
						update(mp[i][res], 1ll * x.second * (m - 4) % P);
					} else if (j != now.cola && j != now.colb) {
						State res = now;
						res.dista = dj, res.cola = j;
						res.dista--, res.distb--;
						update(mp[i][res], x.second);
					}
			} else if (now.distb == 0) {
				for (int j = 1; j <= m && j <= 5; j++)
				for (int dj = 1; dj <= 3; dj++)
					if (j == 5) {
						State res = now;
						res.distb = dj, res.colb = 4;
						if (res.cola == 4) res.colb = 3;
						res.dista--, res.distb--;
						update(mp[i][res], 1ll * x.second * (m - 4) % P);
					} else if (j != now.cola && j != now.colb) {
						State res = now;
						res.distb = dj, res.colb = j;
						res.dista--, res.distb--;
						update(mp[i][res], x.second);
					}
			} else {
				now.dista--, now.distb--;
				update(mp[i][now], x.second);
			}
		}
		for (int i = 1; i <= n; i++)
			update(ans[i], 1ll * mp[i][s.first] * s.second % P);
	}
	LinearSequence :: init(n, ans);
	int finalans = 0;
	for (int i = 1; i * i <= N; i++)
		if (N % i == 0) {
			update(finalans, 1ll * LinearSequence :: query(i) * phi(N / i) % P);
			if (i * i != N) update(finalans, 1ll * LinearSequence :: query(N / i) * phi(i) % P);
		}
	writeln(1ll * finalans * power(N % P, P - 2) % P);
	return 0;
}

【T2】 天涯海角

【思路要点】

• 直接用数据结构难以维护，考虑分块。
• 将每 $K$ 个操作分为一块，对询问涉及的点建立虚树，显然，每个操作只会影响原树上被虚树上的点夹住的整段。
• 对每个整段进行排序 + 去重，即可在 $O(1)$ 的时间内对其进行整体加 $1$ /减 $1$ ，并动态维护答案。
• 时间复杂度 $O(\frac{M}{K}(K^2+NLogN))$ 。
• 取 $K=O(\sqrt{NLogN})$ 时，可得渐进意义下最优时间复杂度 $O(M\sqrt{NLogN})$。
• 注意到$K$个操作至多使得数字的绝对值变化 $K$ ，因此绝对值大于 $K$ 的数在 $K$ 个操作后正负性不变，排序可以使用基数排序，复杂度则降为 $O(\frac{M}{K}(K^2+N))$ 。
• 取 $K=O(\sqrt{N})$ 时，可得渐进意义下最优时间复杂度 $O(M\sqrt{N})$。

【代码】

#include
using namespace std;
const int MAXN = 100005;
const int MAXLOG = 20;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
vector <int> a[MAXN], b[MAXN], c[MAXN];
int n, m, father[MAXN], val[MAXN], q[MAXN];
int timer, dfn[MAXN], depth[MAXN], parent[MAXN][MAXLOG];
int btot, bsize, bl[MAXN], br[MAXN], belong[MAXN];
int ans, size[MAXN], newfa[MAXN], point[MAXN];
bool flg[MAXN];
int lca(int x, int y) {
	if (depth[x] < depth[y]) swap(x, y);
	for (int i = MAXLOG - 1; i >= 0; i--)
		if (depth[parent[x][i]] >= depth[y]) x = parent[x][i];
	if (x == y) return x;
	for (int i = MAXLOG - 1; i >= 0; i--)
		if (parent[x][i] != parent[y][i]) {
			x = parent[x][i];
			y = parent[y][i];
		}
	return father[x];
}
void dfs(int pos, int fa) {
	dfn[pos] = ++timer;
	parent[pos][0] = fa;
	for (int i = 1; i < MAXLOG; i++)
		parent[pos][i] = parent[parent[pos][i - 1]][i - 1];
	depth[pos] = depth[fa] + 1;
	for (unsigned i = 0; i < a[pos].size(); i++)
		dfs(a[pos][i], pos);
}
void calc(int pos) {
	for (unsigned i = 0; i < a[pos].size(); i++) {
		calc(a[pos][i]);
		size[pos] += size[a[pos][i]];
	}
	val[pos] += size[pos];
	if (!flg[pos] && val[pos] <= 0) ans++;
}
bool cmp(int x, int y) {
	return dfn[x] < dfn[y];
}
int main() {
	freopen("evocation.in", "r", stdin);
	freopen("evocation.out", "w", stdout);
	int num; read(num);
	read(n), read(m);
	for (int i = 2; i <= n; i++) {
		read(father[i]);
		a[father[i]].push_back(i);
	}
	for (int i = 1; i <= n; i++)
		read(val[i]), val[i]++;
	static bool in[MAXN];
	memset(in, 0, sizeof(in));
	for (int i = 1; i <= m; i++) {
		read(q[i]), in[q[i]] ^= true;
		if (!in[q[i]]) q[i] = -q[i];
	}
	dfs(1, 0);
	bsize = pow(m, 0.618); btot = 0;
	for (int i = 1; i <= m; i++) {
		if (i % bsize == 1 % bsize) bl[++btot] = i;
		belong[i] = btot, br[btot] = i;
	}
	for (int t = 1; t <= btot; t++) {
		static int tmp[MAXN]; int tot = 0;
		for (int i = bl[t]; i <= br[t]; i++)
			tmp[++tot] = abs(q[i]);
		sort(tmp + 1, tmp + tot + 1, cmp);
		static int stk[MAXN], used[MAXN]; int top = 0, cnt = 0;
		stk[++top] = used[++cnt] = 1;
		for (int i = 1; i <= tot; i++) {
			if (tmp[i] == stk[top]) continue;
			int Lca = lca(tmp[i], stk[top]);
			if (Lca == stk[top]) stk[++top] = used[++cnt] = tmp[i];
			else {
				while (dfn[Lca] < dfn[stk[top - 1]]) {
					newfa[stk[top]] = stk[top - 1];
					top--;
				}
				newfa[stk[top]] = Lca; top--;
				if (Lca == stk[top]) stk[++top] = used[++cnt] = tmp[i];
				else {
					stk[++top] = used[++cnt] = Lca;
					stk[++top] = used[++cnt] = tmp[i];
				}
			}
		}
		while (top >= 2) {
			newfa[stk[top]] = stk[top - 1];
			top--;
		}
		for (int i = 1; i <= cnt; i++) {
			int now = used[i], pos = father[now];
			b[now].clear(), c[now].clear();
			while (pos != newfa[now]) {
				if (!flg[pos]) b[now].push_back(val[pos]);
				pos = father[pos];
			}
			sort(b[now].begin(), b[now].end());
			int top = -1;
			for (unsigned i = 0; i < b[now].size(); i++)
				if (i == 0 || b[now][i] != b[now][i - 1]) b[now][++top] = b[now][i], c[now].push_back(1);
				else c[now][top]++;
			b[now].resize(top + 1);
			point[now] = 0;
			for (unsigned i = 0; i < b[now].size(); i++)
				if (b[now][i] <= 0) point[now]++;
				else break;
		}
		memset(size, 0, sizeof(size));
		for (int i = bl[t]; i <= br[t]; i++) {
			int now = abs(q[i]);
			if (q[i] >= 0) {
				if (val[now] + size[now] <= 0) ans--; flg[now] = true;
				int pos = now;
				while (pos) {
					size[pos]--;
					if (!flg[pos] && val[pos] + size[pos] == 0) ans++;
					if (point[pos] < b[pos].size() && b[pos][point[pos]] + size[pos] <= 0) ans += c[pos][point[pos]++];
					pos = newfa[pos];
				}
			} else {
				if (val[now] + size[now] + 1 <= 0) ans++; flg[now] = false;
				int pos = now;
				while (pos) {
					if (now != pos && !flg[pos] && val[pos] + size[pos] == 0) ans--;
					size[pos]++;
					if (point[pos] > 0 && b[pos][point[pos] - 1] + size[pos] > 0) ans -= c[pos][--point[pos]];
					pos = newfa[pos];
				}
			}
			printf("%d ", ans);
		}
		ans = 0; memset(size, 0, sizeof(size));
		for (int i = bl[t]; i <= br[t]; i++)
			if (q[i] >= 0) size[q[i]]--, flg[q[i]] = true;
			else size[-q[i]]++, flg[-q[i]] = false;
		calc(1);
	}
	return 0;
}

【T3】 无畏永恒

【思路要点】

• 将问题稍作修改，设定一个目标位置，判断能否将一点灵力移动至目标位置。

• 令坐标 $(x,y)$ 距离目标位置的曼哈顿距离为 $d_{x,y}$ ，我们希望为每一个坐标设定一个权值 $v_{x,y}$ ，使得一次操作不会使局面的权值和增大，且一次正向移动，即消耗 $d_{i,j}$ 的值为 $a,a+1$ 的两点灵力，产生一点 $d_{i,j}$ 的值为 $a-1$ 的灵力的移动不会使得局面的权值和变化。

• 则应当令 $v_{x,y}={\phi }^{d_{x,y}}$ ，其中 ${\phi }^2+\phi =1,\phi =\frac{\sqrt{5}-1}{2}$ 。

• 最终状态的权值和为 $1$ ，要想在有限步内达到最终状态，起始状态的权值和应当严格大于 $1$ 。

• 因此，令 $N_{max}$ 为满足如下不等式的最大的 $N$ ，答案存在上界 $N_{max}$ 。 $${\phi }^N\sum _{i=1}^{+\infty }{i}^N{\phi }^{i-1}\sum _{j=-\infty }^{+\infty }{\phi }^{|j|}\ge 1$$

• 下面证明：若每一列的灵力的数量从右到左单调不降，上界 $N_{max}$ 可以取到。

• 假设目标位置位于第 $N$ 列，那么当前局面的权值应当为 $${\phi }^N\sum _{i=1}^{+\infty }{i}^N{\phi }^{i-1}\sum _{j=-\infty }^{+\infty }{\phi }^{|j|}$$

• 注意到 $$\sum _{j=-\infty }^{+\infty }{\phi }^{|j|}=1+2\sum _{j=1}^{+\infty }{\phi }^j=1+\frac{2\phi }{1-\phi }={\phi }^{-3}$$

• 当前局面的权值同样可以写为 $${\phi }^{N-3}\sum _{i=1}^{+\infty }{i}^N{\phi }^{i-1}$$

• 该值与局面 “将目标位置所在行的灵力向前移动三格，删去其余行的灵力” 后的局面相同。

• 令 $R_k$ 表示转化后局面最靠前的 $k$ 列。

• 下面证明两点：
  $(1)$ 、对于任意 $k<\infty$ ， $R_k$ 能够被转化前的局面到达。
  $(2)$ 、对于任意使得初始局面权值和大于 $1$ 的目标位置，存在 $k<\infty$ ，使得 $R_k$ 可以到达目标位置。

• 证明 $(1)$ ：
  考虑将过程反转，当前局面为 $R_k$ ，
  每次操作可以将一点灵力移动，并在相邻位置产生一点新的灵力，
  要求得到一个每一格上的灵力数均不超过初始状态中该格的灵力数的局面。
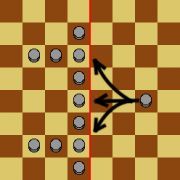
  任意一点 $R_k$ 中的灵力都可以在 $3$ 列之外制造一个如下图的局面：
  
  并且竖直的部分可以任意长，
  水平突出部分始终在竖直部分的头尾向内一行延伸出 $2$ 格。
  由于竖直的部分可以任意长，
  我们可以让 $R_k$ 中每一格中的灵力形成的该结构互不相交。
  又因为每一列的灵力的数量从右到左单调不降，
  得到的局面每一格上的灵力数均不超过初始状态中该格的灵力数。

• 证明 $(2)$ ：
  取任意 $x$ 满足 $R_x$ 的权值和大于 $1$ 。
  依然考虑将过程反转，从目标状态出发，向左移动灵力，产生前后两堆灵力。
  设靠左的一堆灵力数为 $a$ ，靠右的一堆灵力数为 $b$ 。
  若当前靠右的一堆灵力所在的格子在 $R_x$ 中有 $c$ 点灵力，
  则我们可以在这一格留下 $Min\{b,c\}$ 点灵力，将剩余灵力向左移动，
  此后靠左的一堆灵力数为 $b-Min\{b,c\}$ ，靠右的灵力数为 $a+b-Min\{b,c\}$ ，
  不难发现整个过程中 $a$ 始终小于等于 $b$ 。
  在 $x$ 或之前的某一时刻，靠右的一堆灵力数将不大于 $c$ ，
  此时由于 $a\le b$ ，靠左的一堆灵力数同样不会大于所在位置需要的灵力数，
  因此尽管 $R_x$ 不一定可以到达目标状态， $R_{x+1}$ 一定可以到达目标状态。

• 以上证明过程同样给出了构造方法。

• 那么，记 $$F(N)={\phi }^{-4}\sum _{i=1}^{+\infty }{i}^N{\phi }^i$$

• 有 $$Ans=\lfloor Lo{g}_{{\phi }^{-1}}F(N)\rfloor =\lfloor \frac{ln(F(N))}{ln({\phi }^{-1})}\rfloor$$

• 关于 $F(N)$ 的计算可以采用 Γ函数 的斯特林近似：

• 当 $0<\phi <1$ 且 $n>>1$ ，有
  $${\mathrm{L}\mathrm{i}}_{-n}(\phi )=\sum _{i=1}^{\infty }{i}^n{\phi }^i\approx {\int }_1^{\infty }{x}^n{\phi }^{x}dx\approx {\int }_0^{\infty }{x}^n{\phi }^{x}dx=\frac{\Gamma (n+1)}{(-\log \phi {)}^{n+1}}\approx \frac{\sqrt{2\pi n}{n}^n{e}^{-n}}{(-\log \phi {)}^{n+1}}.$$

• 则可较为准确地得到 $ln(F(N))$ 的近似值。

• 当然，作为考场得分的方式，直接根据$F(N)$的定义式计算前若干项也是可以的。

【代码】

#include
using namespace std;
const int MAXN = 2e5 + 5;
const double pi = acos(-1);
const double phi = (sqrt(5) - 1) / 2;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
const int MAXP = 25, P = 1e9;
struct INT {
	int len, a[MAXP];
	INT () {
		len = 1;
		memset(a, 0, sizeof(a));
	}
	INT (int num) {
		assert(num < P);
		len = 1;
		memset(a, 0, sizeof(a));
		a[0] = num;
	}
};
bool operator < (const INT &x, const INT &y) {
	if (x.len < y.len) return true;
	if (x.len > y.len) return false;
	for (int i = x.len - 1; i >= 0; i--) {
		if (x.a[i] < y.a[i]) return true;
		if (x.a[i] > y.a[i]) return false;
	}
	return false;
}
bool operator > (const INT &x, const INT &y) {
	if (x.len > y.len) return true;
	if (x.len < y.len) return false;
	for (int i = x.len - 1; i >= 0; i--) {
		if (x.a[i] > y.a[i]) return true;
		if (x.a[i] < y.a[i]) return false;
	}
	return false;
}
bool operator <= (const INT &x, const INT &y) {
	if (x.len < y.len) return true;
	if (x.len > y.len) return false;
	for (int i = x.len - 1; i >= 0; i--) {
		if (x.a[i] < y.a[i]) return true;
		if (x.a[i] > y.a[i]) return false;
	}
	return true;
}
bool operator >= (const INT &x, const INT &y) {
	if (x.len > y.len) return true;
	if (x.len < y.len) return false;
	for (int i = x.len - 1; i >= 0; i--) {
		if (x.a[i] > y.a[i]) return true;
		if (x.a[i] < y.a[i]) return false;
	}
	return true;
}
bool operator == (const INT &x, const INT &y) {
	if (x.len != y.len) return false;
	for (int i = x.len - 1; i >= 0; i--)
		if (x.a[i] != y.a[i]) return false;
	return true;
}
bool operator != (const INT &x, const INT &y) {
	if (x.len != y.len) return true;
	for (int i = x.len - 1; i >= 0; i--)
		if (x.a[i] != y.a[i]) return true;
	return false;
}
INT operator + (const INT &x, const INT &y) {
	INT res;
	res.len = max(x.len, y.len) + 1;
	for (int i = 0; i < res.len; i++) {
		res.a[i] += x.a[i] + y.a[i];
		if (res.a[i] >= P) {
			res.a[i + 1] += res.a[i] / P;
			res.a[i] %= P;
		}
	}
	while (res.len >= 2 && res.a[res.len - 1] == 0) res.len--;
	return res;
}
INT operator += (INT &x, const INT &y) {
	x = x + y;
	return x;
}
INT operator - (const INT &x, const INT &y) {
	INT res; assert(x >= y);
	res.len = x.len;
	for (int i = 0; i < res.len; i++) {
		res.a[i] += x.a[i] - y.a[i];
		if (res.a[i] < 0) {
			res.a[i + 1] += res.a[i] / P;
			res.a[i] %= P;
			if (res.a[i] < 0) {
				res.a[i + 1] -= 1;
				res.a[i] += P;
			}
		}
	}
	while (res.len >= 2 && res.a[res.len - 1] == 0) res.len--;
	return res;
}
INT operator -= (INT &x, const INT &y) {
	x = x - y;
	return x;
}
INT operator * (const INT &x, const INT &y) {
	INT res;
	res.len = x.len + y.len;
	static long long tres[MAXP];
	memset(tres, 0, sizeof(tres));
	for (int i = 0; i < x.len; i++)
	for (int j = 0; j < y.len; j++) {
		long long tmp = 1ll * x.a[i] * y.a[j];
		tres[i + j] += tmp % P;
		tres[i + j + 1] += tmp / P;
	}
	for (int i = 0; i < res.len; i++) {
		tres[i + 1] += tres[i] / P; 
		res.a[i] = tres[i] % P;
	}
	while (res.len >= 2 && res.a[res.len - 1] == 0) res.len--;
	return res;
}
INT operator *= (INT &x, const INT &y) {
	x = x * y;
	return x;
}
INT operator / (const INT &x, const int &y) {
	INT res; ll rem = 0;
	res.len = x.len;
	for (int i = x.len - 1; i >= 0; i--) {
		rem += x.a[i];
		res.a[i] = rem / y;
		rem = rem % y * P;
	}
	while (res.len >= 2 && res.a[res.len - 1] == 0) res.len--;
	return res;
}
INT operator /= (INT &x, const int &y) {
	x = x / y;
	return x;
}
int operator % (const INT &x, const int &y) {
	int ans = x.a[x.len - 1] % y;
	for (int i = x.len - 2; i >= 0; i--)
		ans = (1ll * P * ans + x.a[i]) % y;
	return ans;
}
INT operator %= (INT &x, const int &y) {
	x = x % y;
	return x;
}
void print(const INT &x) {
	printf("%d", x.a[x.len - 1]);
	for (int i = x.len - 2; i >= 0; i--)
		printf("%09d", x.a[i]);
	printf("\n");
}
int getans(int n) {
	if (n == 0) return 4;
	double ans = -4 * log(phi);
	ans += log(sqrt(2 * pi * n)) + n * log(n) - n;
	ans -= (n + 1) * log(-log(phi));
	return (int) (ans / -log(phi));
}
INT power(INT x, int y) {
	if (y == 0) return 1;
	INT tmp = power(x, y / 2);
	if (y % 2 == 0) return tmp * tmp;
	else return tmp * tmp * x;
}
struct info {int xa, ya, xb, yb, xc, yc; INT x; };
vector <info> ans;
INT goal[MAXN];
int main() {
	freopen("eternity.in", "r", stdin);
	freopen("eternity.out", "w", stdout);
	int type, n, Max;
	read(type), read(n);
	Max = getans(n);
	if (type == 2) {
		printf("%d\n", Max);
		return 0;
	}
	INT a = 1, b = 0; int cnt = 0;
	for (int i = 4 - Max; true; i++) {
		INT now = 0;
		if (i >= 1) {
			now = power(i, n);
			goal[i] = min(a, now);
			a -= min(a, now);
		}
		if (a == 0) {
			cnt = i + 1;
			goal[i + 1] = b;
			break;
		}
		ans.push_back((info) {-i + 2, 0, -i + 1, 0, -i + 3, 0, a});
		b += a, swap(a, b);
	}
	int extend = 0;
	for (int i = cnt; i >= 1; i--, extend += 2) {
		int x = -i + 3;
		ans.push_back((info) {x - 1, 0, x - 1, 1, x, 0, goal[i]});
		ans.push_back((info) {x - 2, 0, x - 2, -1, x - 1, 0, goal[i]});
		ans.push_back((info) {x - 2, 1, x - 2, 2, x - 1, 1, goal[i]});
		ans.push_back((info) {x - 3, -1, x - 3, -2, x - 2, -1, goal[i]});
		ans.push_back((info) {x - 3, 0, x - 3, -1, x - 2, 0, goal[i]});
		ans.push_back((info) {x - 3, 1, x - 3, 2, x - 2, 1, goal[i]});
		ans.push_back((info) {x - 3, 2, x - 3, 3, x - 2, 2, goal[i]});
		int a = 2, b = -1;
		for (int j = 1; j <= extend; j++, a++, b--) {
			ans.push_back((info) {x - 3, a + 1, x - 3, a + 2, x - 3, a, goal[i]});
			ans.push_back((info) {x - 3, b - 1, x - 3, b - 2, x - 3, b, goal[i]});
		}
		ans.push_back((info) {x - 4, a, x - 5, a, x - 3, a, goal[i]});
		ans.push_back((info) {x - 4, b, x - 5, b, x - 3, b, goal[i]});
	}
	reverse(ans.begin(), ans.end());
	writeln(ans.size());
	for (auto x : ans) {
		printf("%d %d %d %d %d %d ", x.xa + (x.xa >= 0), x.ya, x.xb + (x.xb >= 0), x.yb, x.xc + (x.xc >= 0), x.yc);
		print(x.x);
	}
	return 0;
}