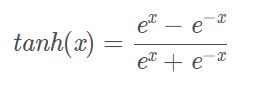激活函数详解
前言
刚入门不久的小白总是会对激活函数产生疑问,它是干什么的?有什么用?有那些常用的激活函数?下面本文就来一一解答。
什么是激活函数
在维基百科中这样解释:在计算网络中, 一个节点的激活函数(Activation Function)定义了该节点在给定的输入或输入的集合下的输出。标准的计算机芯片电路可以看作是根据输入得到开(1)或关(0)输出的数字电路激活函数。这与神经网络中的线性感知机的行为类似。然而,只有非线性激活函数才允许这种网络仅使用少量节点来计算非平凡问题。 在人工神经网络中,这个功能也被称为传递函数。这个解释显得很难理解,那么看一下下面的这张图就很好理解了
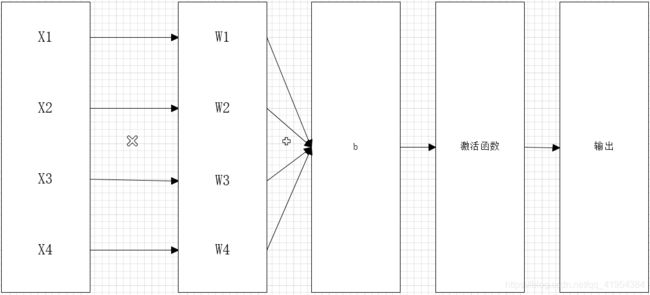
这张图显示的是一个神经元的活动,激活函数的位置就在当前神经元的输出之前,它是一个函数,在经过一系列矩阵运算之后用该函数处理一下,那么上层节点的输出就和下层节点的输入建立了一个联系,这就是激活函数。
激活函数有什么用
大家可以想象一下,如果没有激活函数,那么神经元与神经元之间就像是透明的,每个神经元都进行着函数f(x)=w*x+b的操作,那和线性感知机就没什么区别了,随着神经元数量的增多,由于网络的逼近能力有限,结果会逐渐偏离,所以每个神经元必须要有一个激活函数。他们为神经元提供了模拟复杂非线性数据集所必需的非线性特征。
有哪些常用的激活函数
Sigmoid激活函数
公式如下:
f(z)=1/1+e^-z
几何图形可以用以下代码绘制出来
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
h = np.linspace(-10,10,50)
out = tf.sigmoid(h)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
y = sess.run(out)
plt.xlabel('Activity of Neuron')
plt.ylabel('Output of Neuron')
plt.title('Sigmoidal Activation Function')
plt.plot(h,y)
plt.show()
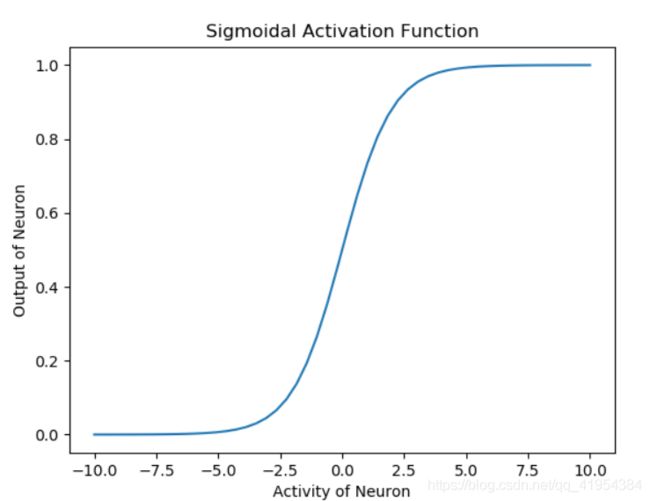
特点:
它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1.
缺点:
sigmoid函数曾经被使用的很多,不过近年来,用它的人越来越少了。主要是因为它固有的一些 缺点。
缺点1:在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失,其中梯度爆炸发生的概率非常小,而梯度消失发生的概率比较大。
tanh()函数
h = np.linspace(-10,10,50)
out = tf.tanh(h)#计算双曲正切值的函数
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
y = sess.run(out)
plt.xlabel('Activity of Neuron')
plt.ylabel('Output of Neuron')
plt.title('Hyperbolic Tangent Activition Funiction')
plt.plot(h,y)
plt.show()
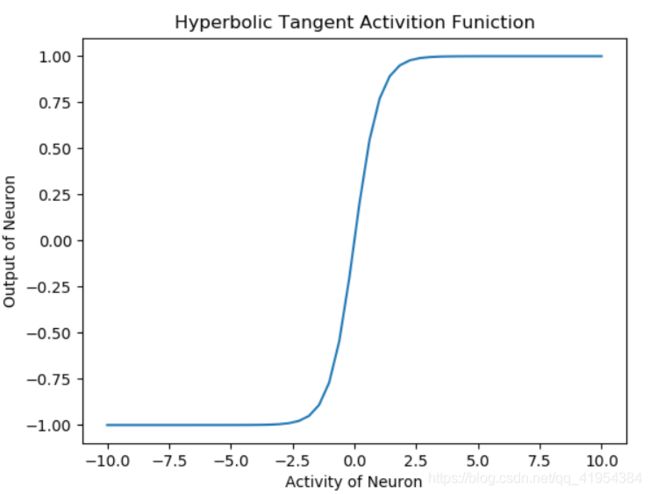
双曲正切激活函数在形状上是 S 形并具有非线性特性。该函数以 0 为中心,与 Sigmoid 函数相比具有更陡峭的导数。与 Sigmoid 函数一样,它也受到梯度消失问题的影响。
Relu激活函数
公式如下:
Relu = max(0,x)
几何图形可以用以下代码绘制出来(引用的库同上)
h = np.linspace(-10,10,50)
out = tf.nn.relu(h)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
y = sess.run(out)
plt.xlabel('Activity of Neuron')
plt.ylabel('Output of Neuron')
plt.title('ReLU Activation Funiction')
plt.plot(h,y)
plt.show()
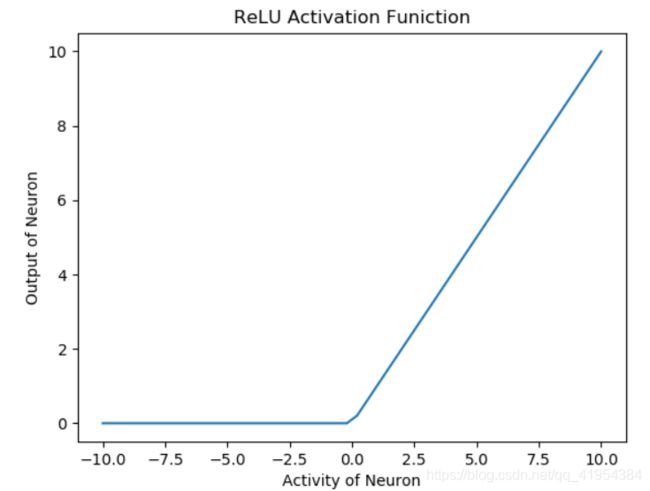
使用 ReLU 的主要优点之一是导致稀疏激活。在任何时刻,所有神经元的负的输入值都不会激活神经元。就计算量来说,这使得网络在计算方面更轻便。
ReLU 神经元存在死亡 ReLU 的问题,也就是说,那些没有激活的神经元的梯度为零,因此将无法进行任何训练,并停留在死亡状态。尽管存在这个问题,但 ReLU 仍是隐藏层最常用的激活函数之一。
Softmax激活函数
公式如下:
f(x)=max(ax,x)
几何图形可以用以下代码绘制出来(引用的库同上)
h = np.linspace(-5,5,50)
out = tf.nn.softmax(h)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
y = sess.run(out)
plt.xlabel('Activity of Neuron')
plt.ylabel('Output of Neuron')
plt.title('Softmax Activition Funiction')
plt.plot(h,y)
plt.show()
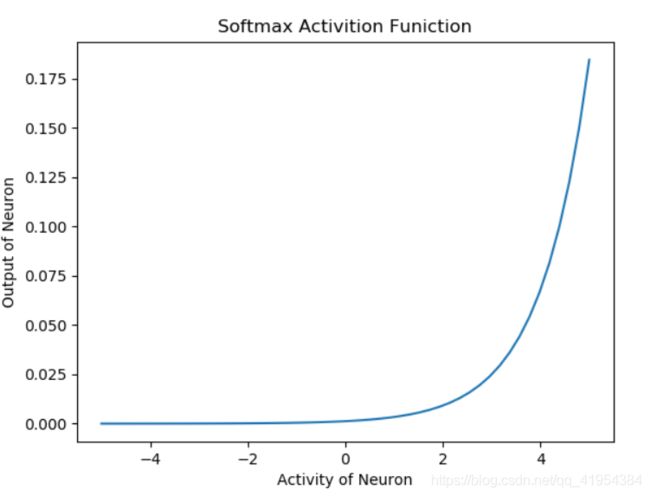
Softmax 激活函数被广泛用作输出层的激活函数,该函数的范围是 [0,1]。在多类分类问题中,它被用来表示一个类的概率。所有单位输出和总是 1。
总结
可以使用的激活函数有很多,但是使用的时候要根据自己的需求找到那个最适合自己的。根据手头的任务来看,一般来说,隐藏层最好使用 ReLU 神经元。对于分类任务,Softmax 通常是更好的选择;对于回归问题,最好使用 Sigmoid 函数或双曲正切函数。