回溯法_树的遍历_N皇后问题_幂集合问题_有多少种解码方式的问题_遍历状态树_分叉(选择)有限的情况
目录
1.回溯法
2.求集合的幂集
3.N皇后问题
3.1N后问题递归
3.2N皇后问题(循环)
4.编程题:有多少种解码方式(求解组合数问题)
5.待补充:
1.回溯法
程序设计中,有一类求解一组解、求解全部解、或求解最优解的问题。如8皇后问题(N皇后问题)
这类问题不是根据某种确定的计算法则去运算,而是每次都利用试探和回溯(Backtracking)的搜索技术进行求解的!
回溯法是设计递归过程的一种重要的方法!它的求解过程实质上是一个遍历一颗“状态树”的过程,只是这颗树不是在遍历前就预先建立好的,而是隐含在遍历的过程中建立出来的。
要认识到这一点,对很多问题的递归过程的设计问题也就清楚了!
回溯法有“通用的解题法“之称,用它可以系统地搜索一个问题的所有解或任意解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在包含问题的所有解的解空间树中,按照深度优先的搜索策略,从根结点出发搜索解空间树。
算法搜索至解空间中的任意结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先的策略进行搜索。
回溯法用来求问题的所有解时要回溯到根,且根结点的所有子树都已经搜索遍才结束;
而用来求任意解时,只需要搜索到问题的一个解就可以结束。
这种以深度优先的方式系统地遍历搜索问题的解的方法称为回溯法,适用于解一些组合数较大的问题!
2.求集合的幂集
例1:求含n个元素的几个的幂集合。
一个集合A的幂集合是有A的所有子集组成的集合。
A={1,2,3},则A的幂集为:![]()
幂集的每一个元素是一个集合,它或者是一个空集,或者含有集合A中的若干的元素组成的集合,或者等于A。
问题的转化:
对于A的幂集中的某个元素集合,从A集合每个元素的角度反之看待:A中的元素在A的幂集的某个元素子集中只有两种状态:
它或者属于幂集的这个元素集合,或者不属于幂集的这个元素集合,
则求幂集某个元素集合的过程可以依次对集合A中的元素进行“取”或“舍”的过程!
我们可以用一颗二叉树(就两种选择,属于还是不属于,非左即右的过程)
来表示这个选取的过程中幂集元素集合状态的变化过程:
因此求集合幂集合的过程就可看作是先序遍历这棵二叉树的过程:
void GetPowerSet(int i, vector A, vector& B, vector>& powerSet)
{/*线性表A表示集合A,线性表B表示A的幂集的某个元素集合
局部变量k表示进入函数时表B的当前长度(所含元素个数)
第一次调用该函数时B是空表,k=0;i=0
powerSet是个二维向量,每一行用来存储幂集的一个元素集合
*/
/*A的幂集的元素集合最大的一个应该就是A原集,所有改函数递归调用i=0,1,2,3就到达叶子节点了!
然后就应该退栈返回(回溯)*/
if (i >= A.size())//
{
powerSet.push_back(B);
}
else
{
int x = A[i];
//int k = B.size();
B.push_back(x);//取
GetPowerSet(i + 1, A, B, powerSet);
B.pop_back();//舍
GetPowerSet(i + 1, A, B, powerSet);
}
}
测试用例:
#include "stdafx.h"
#include
#include
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
int MyArray[3] = { 1, 2, 3 };
vector A(MyArray, MyArray+3);
vector B;
int i = 0;
vector> powerSet;
GetPowerSet(i, A, B, powerSet);
cout << "powerSet.size()=" << powerSet.size() << endl;
for (int i = 0; i < powerSet.size(); i++)
{
for (auto ele : powerSet[i])
{
cout << ele << " ";
}
cout << endl;
}
system("pause");
return 0;
}
输出结果:
powerSet.size()=8
1 2 3
1 2
1 3
1
2 3
2
3
请按任意键继续. . .3.N皇后问题
3.1 4皇后
4*4的棋盘,在里面放4个皇后,保证任意两个皇后都不在
a.同一行
b.同一列
c.同一对角线
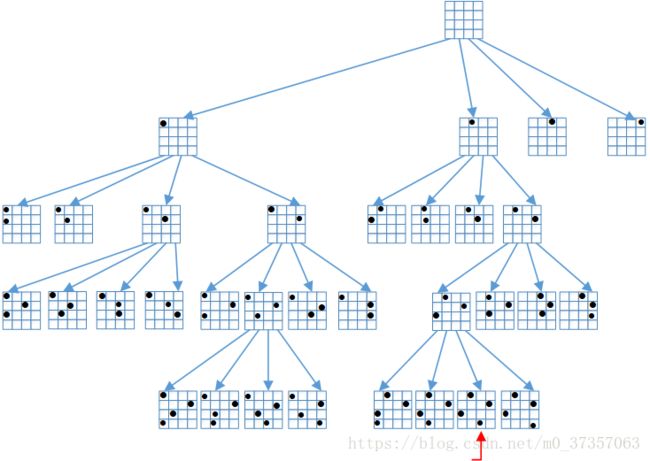
下图是4皇后问题的棋盘状态树(四叉树)
3.1N后问题递归
下面给出以递归的方式,深度优先遍历这个四叉状态树:
#include "stdafx.h"
#include
using namespace std;
//四皇后问题
/*数组gFourQueen的i元素代表在棋盘(二维数组)的i行、gFourQueen[i]列的位置放置皇后
gCount用于对解的个数进行计数!*/
static int gFourQueen[4] = { 0 }, gCount = 0;
void print()//输出每一种情况下棋盘中皇后的摆放情况
{
for (int i = 0; i < 4; i++)
{
int inner;
for (inner = 0; inner < gFourQueen[i]; inner++)
cout << "0";
cout << "#";
for (inner = gFourQueen[i] + 1; inner < 4; inner++)
cout << "0";
cout << endl;
}
cout << "==========================\n";
}
int check_pos_valid(int loop, int value)
{//检查是否存在有多个皇后在同一行/列/对角线的情况
int index;
int data;
for (index = 0; index < loop; index++)
{
data = gFourQueen[index];
if (value == data)
return 0;
if ((index + data) == (loop + value))
return 0;
if ((index - data) == (loop - value))
return 0;
}
return 1;
}
void four_queen(int index)
{//在index行(index=0,1,2,3)找皇后的合适放位置gFourQueen[index]列
int loop;
for (loop = 0; loop < 4; loop++)
{
if (check_pos_valid(index, loop))
{//检查棋盘的index行loop列是否可以放置一个皇后
gFourQueen[index] = loop;//棋盘的index行loop列放置一个皇后
if (3 == index)//注意idex下标是从0计起的!
{//3==index代表最后一行的皇后已经放置,已经得到一个解
gCount++, print();
gFourQueen[index] = 0;
return;
}
four_queen(index + 1);
gFourQueen[index] = 0;
}
}
}
int main(int argc, char*argv[])
{
four_queen(0);
cout << "total=" << gCount << endl;
system("pause");
return 0;
} 输出:
0#00
000#
#000
00#0
==========================
00#0
#000
000#
0#00
==========================
total=2
请按任意键继续. . .
求解的过程从空棋盘开始,设在第1行至第m行都已经正确地放置了m个皇后,现在尝试在第m+1行上找合适的位置放置第m+1个皇后,如果都存在这样合理的位置,直到第n行也找到了合适的位置放了第n个皇后,就找到了一个解。
接着改变第n行上皇后的位置,期望得到下一组解。z
在任意行上有n种可能的列可供选择,依次尝试第1,第2,...,第n列,当这n列都尝试完都没找到合适的位置时,说明该行不存在合适的位置,需要回溯到上一行(即去改变上一个皇后的放置位置)
N皇后的限界函数就是皇后的放置规则,如下:
bool Place(vector& Column, int index)
{
int i;
for (i = 1; i < index; i++)
{
int Column_differ = abs(Column[index] - Column[i]);
int Row_differ = abs(index - i);
if (Column[i] == Column[index] || Column_differ == Row_differ)
{
return false;
}
}
return true;
}
3.2N皇后问题(循环)
下面给出4皇后问题的非递归(循环)方式求解:
void N_Queue(int n)//n皇后问题
{
//static const int N = n;
//int* Column_Num = new int[n+1]();
//int Column_Num[N];//错误:数组大小应输入常量表达式
vector Column_Num(10, 0);
int index = 1;
//int i;
int answer_num = 0;
//for (int i = 1; i <= n; i++)
//{//对Column_Num进行初始化
// Column_Num[i] = 0;
//}
/*思考是怎么找到所有解以后是怎么退出while(index>0)循环的,
当然index会由1减到0,然后结束while循环
这个含义就是,在找到了所有解中的最后一组解时,当再尝试有没有下一组解的过程中,
index从n回退(回溯)到了1(即回溯到了解空间的根),
发现第一个皇后在第一行的所有列的位置都已经尝试遍了,
那么在此次wihle循环中index--,index=0,即退出while循环。
*/
while (index > 0)
{/*这里有了默认的放置顺序,即第一个皇后放在第一行,第二个皇后放在第二行...,
如果能再第n行放下第n个皇后,则说明成功找到一个解*/
//第index个皇后都是从第index行的第一列进行尝试的!
Column_Num[index]++;/*初始进入时候index=1,Column_Num[index]++后等于1,即第一个皇后放在第一行的第一列*/
while (Column_Num[index] <= n&&!Place(Column_Num, index))
{/*寻第index个皇后的位置:在第Column_Num[index]列放不了,就放在下一列:即Column_Num[index]++列!*/
Column_Num[index]++;
}
/*
这里的Column_Num[index]就是对第index个皇后放置第index行的哪一列进行试探查找,
放在第Column_Num[index]列,
如果Column_Num[index]>n了,说明这个皇后在第index行没法放下去,
得回溯到上一个皇后,即index-- 回溯到上一个皇后
*/
if (Column_Num[index] <= n)
{
if (index == n)/*最后一个皇后放置成功*/
{
answer_num++;
/*不要这组循环Column_Num[index]自增语句也行啊!,
外面的大while(index>0)里的第一条语句Column_Num[index]++;保证了下一次Column_Num[index] > n,,
走index--分支!*/
//for (int i = 1; i <= n; i++)
//{//这个是干嘛的?!,,找到一个(组)解了以后,要去找下一个(组)解!
// Column_Num[index]++;
//}
}
else/*继续寻找下一个皇后的位置*/
{
index++;
Column_Num[index] = 0;
}
}
else
{/*当前皇后无法放置,回溯到上一个皇后*/
index--;
}
}
cout << "answer_num=" << answer_num << endl;
} 测试例子:
int _tmain(int argc, _TCHAR* argv[])
{
N_Queue(8);
system("pause");
return 0;
}
输出:
answer_num=924.编程题:有多少种解码方式(求解组合数问题)
编程题2:
一条由26个字母组成的字符串,经加密成数字流,加密规则:
‘A’->1
‘B’->2
...
‘Z’->26
现给定一密文,判断有多少种解密方式:
如:
“12”;有两种解密方式:AB;L
再如:
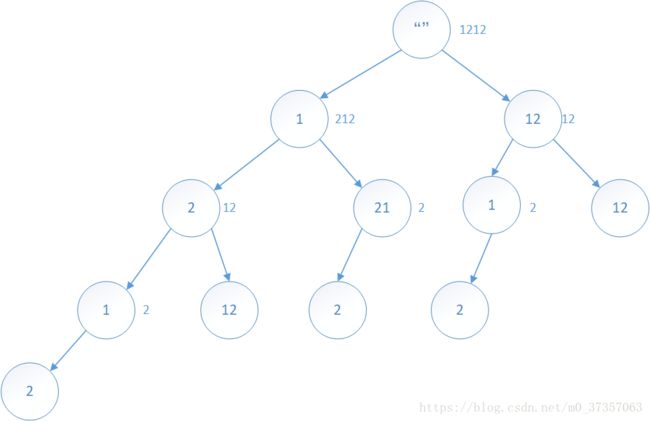
“1212”有5种解密方式:
1:1-2-1-2
2:12-12
3:1-21-2
4:12-1-2
5:1-2-12
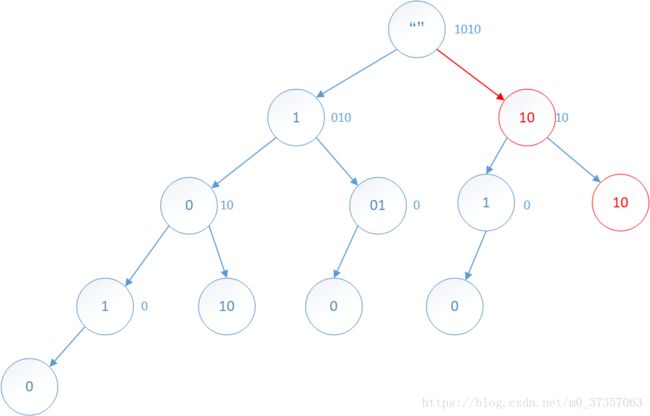
0是特殊情况:
"1010"就只能有一种解码方式:10-10
从字符串的头开始,每次要么取一个字符,要么取两个字符,非1即2的选择问题!
根节点是完整的字符串1212,根节点输出空串,根节点以完整串1212分别调用左/右子树进行划分:
向左走是输出一个字符,向右走是输出两个字符,直到叶子节点输出所有字符,串为空为止!
边构造一棵二叉树的过程就可以得到所有的解码方式,其中判断没一种方式是否可解码(合理),若合理,则正确的解码方式计数加1:
考虑含有0 的特殊情况:
下面是二叉树结点的定义:
/*二叉树的结点存储结构,二叉链表存储结构*/
typedef struct BiTNode{
string data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
/*
BiTNode:是结构类型
BiTree:是指向结点BiTNode的指针类型
*/下面是构造这样一棵解码树的递归的方法:
//不要树BiTree& T也可以,只是用树的话画图看上去概念清晰,递归的进入与返回好看
void CreateBiTree(BiTree& T, string str,int dir,int& count)
{
if (str.empty())
{
T = nullptr;
return;
}
else
{
if (dir == 0)//整颗树的根结点
{
T = new BiTNode;
T->data = "";//根结点赋值为空字符串
if (str.size() > 0)
{//至少有1个字符
CreateBiTree(T->lchild, str, 1,count);
}
if (str.size() > 1)
{//至少有2个字符
CreateBiTree(T->rchild, str, 2, count);
}
}
if (dir == 1)//向左走,取1个数字
{
if (str.size() < 1)
{
T = nullptr;
return;//这return 有没有效果一样
}
else
{
T = new BiTNode;
T->data = str.substr(0, 1);
int data = std::stoi(T->data);
if (data < 1 || data > 26)
{
return;
}
str = str.substr(1, string::npos);
if (str.empty())
{
count++;
}
//if (str.size() > 0)
//{
CreateBiTree(T->lchild, str, 1, count);
//}
//if (str.size() > 1)
//{
CreateBiTree(T->rchild, str, 2, count);
//}
}
}
else if (dir == 2)//向右走,取2个数字
{
if (str.size() < 2)
{
T = nullptr;
return;//这return 有没有效果一样
}
else
{
T = new BiTNode;
T->data = str.substr(0, 2);
if (T->data[0] == '0')
{//考虑"0X"这种特殊情况
return;
}
int data = std::stoi(T->data);
if (data < 1 || data > 26)
{
return;
}
str = str.substr(2, string::npos);
if (str.empty())
{
count++;
}
//if (str.size() > 0)
//{
CreateBiTree(T->lchild, str, 1, count);
//}
//if (str.size() > 1)
//{
CreateBiTree(T->rchild, str, 2, count);
//}
}
}
}
return;
}下面是测试代码:
#include "stdafx.h"
#include
#include
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
string str = "12";//1212
//string substr = str.substr(0, 1);
//cout << "substr=" << substr << endl;
//string substr2 = str.substr(4, string::npos);
//cout << substr2.size() << endl;
BiTree T= nullptr;
int count = 0;
CreateBiTree(T, str, 0, count);
cout << "count=" << count << endl;
system("pause");
return 0;
}
输出:
count=5
请按任意键继续. . .
5.待补充:
1.回溯法
问题的解空间
回溯法的基本思想
回溯法的计算框架(递归于非递归)
回溯法的限界函数(减枝)
2.例子
使用回溯法的例子:
0-1背包问题、迷宫问题、骑士游历问题、选最优解问题等
数据结构 树的遍历 回溯法 N皇后问题 多少种解码方式问题