最近为了找实习开始做一些练手的编程,刚好在复习深度学习基础的时候,遇到了吴恩达和李宏毅两位大神,讲课讲得好真的很重要,废话不多说,下面开始我们的第一份编程练习。
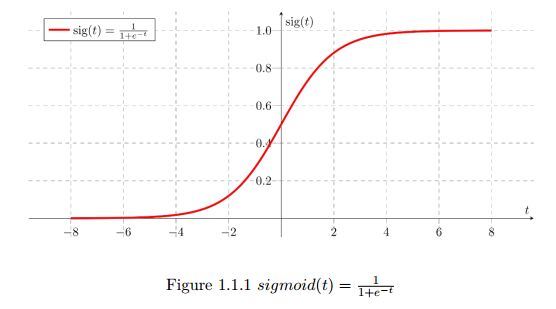
首先我们要实现的是sigmoid激活函数,也就是逻辑回归的function,个人建议学习深度学习从逻辑回归开始,虽然到最后基本没有人在自己的神经网络里面使用这个激活函数了,但是它还是深度学习开始的地方。
sigmoid
ps:它的梯度峰值是0.25
math库实现
import math
def basic_sigmoid(x):
s = 1/(1+math.exp(-x))
return s
虽然可以这样实现,但是我们深度学习希望能够很好的处理向量而不是像这样还需要写一个for循环,去给向量中的每个值去计算一个值,那样就太浪费时间啦!
numpy库实现
In [1]: import numpy as np
In [2]: x = np.array([1,2,3])
In [3]: print(np.exp(x))
[ 2.71828183 7.3890561 20.08553692]
numpy可以实现优秀的向量计算
In [4]: import numpy as np
...:
...: def sigmoid(x):
...: s = 1/(1+np.exp(-x))
...: return s
...:
...: x = np.array([1,2,3])
...:
...: print(sigmoid(x))
...:
[ 0.73105858 0.88079708 0.95257413]
sigmoid梯度
计算公式:
In [5]: def sigmoid_derivative(x):
...: s = 1/(1+np.exp(-x))
...: ds = s*(1-s)
...: return ds
维度的转换
v = v.reshape((v.shape[0]*v.shape[1], v.shape[2]))
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
### START CODE HERE ### ( 1 line of code)
v = image.reshape((image.shape[0]*image.shape[1]*image.shape[2]),1)
### END CODE HERE ###
return v
数据的归一化
例如:x/||x||
In [1]: import numpy as np
In [6]: def normalizeRows(x):
...: x_norm = np.linalg.norm(x,axis=1,keepdims=True)
...: x = x/x_norm
...: return x
...:
In [7]: x = np.array([[0,3,4],[1,6,4]])
In [8]: print(normalizeRows(x))
[[ 0. 0.6 0.8 ]
[ 0.13736056 0.82416338 0.54944226]]
softmax函数
def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp,axis = 1,keepdims = True)
s = x_exp/x_sum
return s
L1、L2正则化
def L1(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
12
Returns:
loss -- the value of the L1 loss function defined above
"""
loss = sum(abs(y-yhat))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
def L2(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L2 loss function defined above
"""
loss = np.dot(y-yhat,y-yhat)
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))