今天郭先生又出来制作游戏了,最近有小伙伴要做一个逻辑转体小游戏,我怎么能不先来试试呢。玩法可以看上面的连接,下面附几张图。线案例请点击博客原文。
游戏规则不懂得可以看自行百度哈,其实玩起来还挺有难度的。关于这个问题,对于新手来说,主要需要克服两个困难。一是这个模型的旋转轴不是固定的,每一次的旋转都是以不同的一个边为轴进行的。二是需要根据关卡数据渲染终点位置和陷阱(这里使用shader)。那么我们今天就来完成第一个难点,如何让几何体动态的绕非定轴转动。我们还是一步一步来。
1. 关卡数据以及其他变量的设置
对于一个闯关类型的游戏,设置好关卡数据和结构是十分必要的,能够让代码简介高效。
var boxes = [], group = new THREE.Group(), box3, uniforms var square = [ { start: [[-1, -1], [-1, -2]], end: [[-1, -4], [-1, -5]], trap: [[-1, -7], [-6, -2]], color: 0xDC210E }, { start: [[-2, -1], [-3, -1], [-2, -2], [-3, -2]], end: [[-5, -6], [-6, -6], [-5, -7], [-6, -7]], trap: [[-1, -7], [-6, -2]], color: 0x097A53 }, { start: [[-1, -1], [-1, -2], [-1, -3], [-2, -1], [-2, -3]], end: [[-1, -6], [-1, -8], [-2, -6], [-2, -7], [-2, -8]], trap: [[-1, -7], [-6, -2]], color: 0x1B2991 } ];
因为不同关卡使用的道具是不一样的,boxes就是盛放每一关小方块的盒子,而绕非定轴转动的主角就是这个group,因为Object3D转动都是绕穿过中心的轴转动的,所以我们需要将小方块放到一个组中,并且让小方块相对组中心产生偏移,这样旋转组,我们看小方格的转动就是绕非定轴的转动了。box3在3D空间中表示一个盒子或立方体。其主要用于表示物体在世界坐标中的边界框,我前面也讲过,不会的也可以往前翻翻,它所能完成的功能,我们通过计算也都可以完成,但是它类似于一个方法类,可以极大的简化我们的计算,稍后我会用到一些。uniforms是向着色器传入一些变量值的,这篇暂时用不到。square储存着每一关的数据,start是初始位置,end是结束位置,trap是陷阱位置,color是小方块的颜色。位置坐标我们稍后再研究。
2. 布局和初始化小方块
首先看一下我是咱们布局的(这个因人而异)。
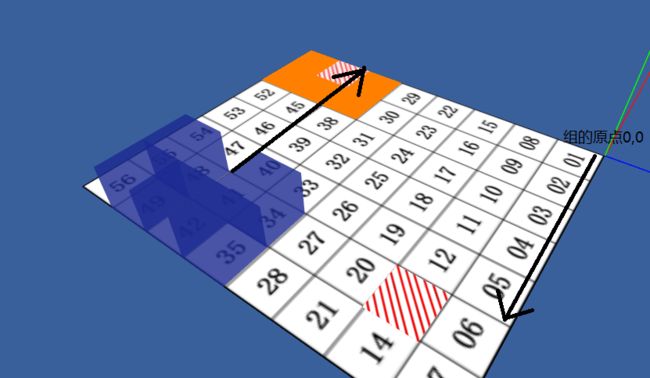
看这个图大家就懂了,我是将逻辑转体的面放在了XOZ面上,并将平面放在了x和z的负半轴,因此他们的坐标都是负值,每一个格子的边长都是10,所以关卡数据start: [[-1, -1], [-1, -2]]代表01格和08格,这样我们就可以将坐标映射到格子上。有了这个映射我们很容易根据数据初始化小方格。
initBox() { let geom = new THREE.BoxGeometry(10, 10, 10); let mate = new THREE.MeshBasicMaterial({color: square[this.game].color, transparent: true, opacity: .8}); let mesh = new THREE.Mesh(geom, mate); boxes = []; square[this.game].start.forEach((d,i) => { let meshCopy = mesh.clone(); meshCopy.position.set(d[0] * 10+ 10 / 2, 10 / 2, d[1] * 10 + 10 / 2); meshCopy.name = 'box-' + i; boxes.push(meshCopy); scene.add(meshCopy) }) this.computedBox3(); },
这段代码比较简单,小做出一个小方块的Mesh,然后根据映射关系,将方块的拷贝放到该放的位置,并将小方块都放在boxes中。在每一关初始化方块后,我们都要计算一下这些小方块集合的box3,因为有了小放块集合很容易得到box3,而有了box3我们又很容易知道小方块集合的边界和中心。
3. 实现非定轴旋转
现在我们有了所有小方块的集合boxes和box3,现在我们就根据上下左右的点击事件实现非定轴转动,先看下图。
就拿这一关来说,假如我们让它向右转,图一的图形会以右下角那条边旋转到图二,下面来看看向右转的代码。
var offset = new THREE.Vector3(box3.max.x, 0, 0); group.position.copy(offset); boxes.forEach(d => { d.position.sub(offset); group.add(d); }) scene.add(group);
这里是最难理解的地方,因为我们的小方格的之前的matrix就已经是matrixWorld了(因为在scene.children中)将他们添加到一个组,再旋转组肯定得不到我们想要的结构(因为新加的组默认还是在原点),所以呢这里我们来了一个乾坤大挪移,将小方格向右移,将组向左移动相同的向量。
这样子小方块就在这个位置了(将入组之后,就相当于在组的这个位置),这样子旋转后,就成了我们想要的样子,而这个向量就是这个offset,box3.max.x是小方块集boxes的x方向的上限。再旋转完之后呢,我们又要把组去掉(这个组就像一个壳一样,转完了就脱掉哈哈)。
awayFromGroup() { boxes.forEach(d => { var trans = new THREE.Vector3(); d.matrixWorld.decompose(trans, new THREE.Quaternion(), new THREE.Vector3()); d.position.copy(trans); d.updateMatrixWorld(); scene.add(d) }) scene.remove(group); this.computedWin(); this.computedBox3(); },
这里我们找到小方块的世界矩阵,找到位置向量trans就可以,然后将小方格重新赋予位置,这里将小方格直接添加到场景中。这样子就完成了乾坤大挪移,其他的方向也都类似哦,别忘了在计算box3哦,因为下一步还要使用哦,
这一篇就先讲绕非定轴转动啦,对于新手来说,这确实需要理解一下,那就先讲到这了,下一篇继续。
转载请注明地址:郭先生的博客