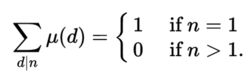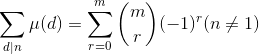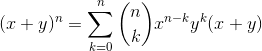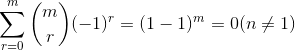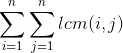莫比乌斯训练报告(随训练更新)

目录

 

莫比乌斯函数简介：

具体运用：

莫比乌斯反演

公式

训练记录：

zoj3435 传送门

bzoj2154 Crash的数字表格

---

莫比乌斯函数简介：

莫比乌斯函数，数论函数，由德国数学家和天文学家莫比乌斯(August Ferdinand Möbius ,1790–1868)提出。梅滕斯(Mertens)首先使用μ(n)作为莫比乌斯函数的记号。而据说，高斯(Gauss)比莫比乌斯早三十年就曾考虑过这个函数。莫比乌斯函数在数论中有着广泛应用。（取自百度百科）

莫比乌斯函数是一个数论函数，它同时也是一个积性函数(i.e.μ(ab) =μ(a)μ(b), a,b互质)

当n不等于1时，n所有因子的莫比乌斯函数值的和为0，

莫比乌斯函数完整定义的通俗表达：

1）莫比乌斯函数μ(n)的定义域是N

2）μ(1)=1

3）当n存在平方因子时，μ(n)=0

4）当n是素数或奇数个不同素数之积时，μ(n)=-1

5）当n是偶数个不同素数之积时，μ(n)=1

具体运用：

参考链接：https://blog.sengxian.com/algorithms/mobius-inversion-formula

证明：当  时有，显然成立。否则设 根据的定义，只需考虑或的情况。我们设 dd 中存在 r 个  为 1，那么有：

由二项式定理：

我们令 x = 1, y = -1，即得证：

此公式运用的很多，在求 或是用杜教筛求前缀和的时候都用的到。

莫比乌斯反演

公式

如果 f(n), g(n)是数论函数，且满足：

则有莫比乌斯反演：

训练记录：

zoj3435 传送门

题意：三维泡泡龙，问消除完全部泡泡所需次数。

思路：求消除完全部泡泡所需次数，其实就是求xyz坐标系中的   三条坐标轴     xoy，xoz，yoz三个面上的对数   求坐标内的对数，求和即可。

#include
using namespace std;
typedef long long ll;
const int N = 1e6 + 7;
const int mod = 1e9 + 7;
bool isprime[N];
int prime[N],cnt,sum[N],mu[N];
ll fpow(ll a,ll b)
{
    ll res = 1;
    while(b){
        if(b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}
void Mobius()
{
    cnt = 0;
    mu[1] = 1;sum[1] = 1;
    for(int i = 2; i < N; ++i){
        if(!isprime[i]){
            prime[++cnt] = i;
            mu[i] = -1;
        }
        for(int j = 1;j <= cnt & i * prime[j] < N; ++j){
            isprime[i * prime[j]] = true;
            if(i % prime[j]== 0){
                mu[i * prime[j]] = 0;
                break;
            }
            mu[i * prime[j]] = -mu[i];
        }
        sum[i] = sum[i - 1] + mu[i];
    }
}
int a,b,c;
int main()
{
    Mobius();
    while(scanf("%d%d%d",&a,&b,&c) != EOF){
        if(c < b) swap(b,c);if(c < a) swap(a,c);if(b < a) swap(a,b);
        a--,b--,c--;
        ll ans = 0;
        if(a) ans++;if(b) ans++;if(c) ans++;
        ll tmp;
        int last,x,y,z;
        for(int i = 1;i <= b;i = last + 1){
            last = i;
            x = a / i,y = b / i,z = c / i;
            if(i <= a){
                last = min(a / x,b / y);
                last = min(last,c / z);
            }
            else last = min(b / y, c / z);
            tmp = (ll) x * y * z + (ll)x * y + (ll)x * z + (ll)y * z;
            ans += tmp * (sum[last] - sum[i - 1]);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

---

bzoj2154 Crash的数字表格

题意：求

思路：

 

#pragma comment(linker, ¡°/STACK:1024000000,1024000000¡±
#include 
using namespace std;
typedef long long ll;
const int N = 1e7 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 20101009;
const int inv2 = 5e8 + 4;
const double eps = 1e-6;
int gcd(int a,int b){return b ? gcd(b,a % b) : a;}
int prime[N],cnt,mu[N];
ll sum[N];
bool vis[N];
void Mobius()
{
    cnt = 0;
    mu[1] = 1;sum[1] = 1;sum[0] = 0;
    for(int i = 2; i < N; ++i){
        if(!vis[i]){
            prime[++cnt] = i;
            mu[i] = -1;
        }
        for(int j = 1; j <= cnt; ++j){
            if(i * prime[j] >= N) break;
            vis[i * prime[j]] = true;
            if(i % prime[j]== 0){
                mu[i * prime[j]] = 0;
                break;
            }
            mu[i * prime[j]] = -mu[i];
        }
        sum[i] = (sum[i - 1] + (ll)mu[i] * i * i) % mod;
    }
}
ll cal(ll a,ll b)
{
    return (a * (a + 1) / 2) % mod * (b * (b + 1) / 2 % mod) % mod;
}
int work(int b,int d)
{
    if(b > d) swap(b, d);
    ll ans = 0,last;
    for(int i = 1; i <= b; i = last + 1){
        last = min(b / (b / i),d / (d / i));
        ans = (ans + (ll)(sum[last] - sum[i - 1]) * cal(b / i,d / i) % mod + mod) % mod;
    }
    return ans;
}
int solve(int b,int d)
{
    if(b > d) swap(b, d);
    ll ans = 0,last;
    for(int i = 1; i <= b; i = last + 1){
        last = min(b / (b / i),d / (d / i));
        ans = (ans + (ll)((last - i + 1) * (last + i) / 2) % mod * (work(b / i,d / i)) % mod + mod) % mod;
    }
    return ans;
}
int n,m;
int main()
{
    Mobius();
    scanf("%d%d",&n,&m);
    printf("%d\n",solve(n,m));
    return 0;
}