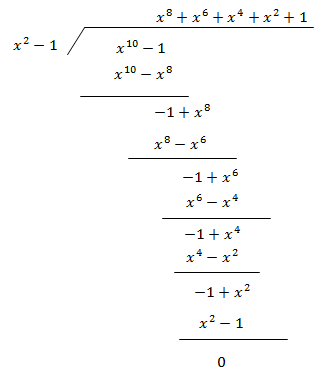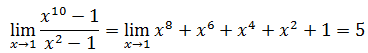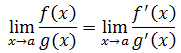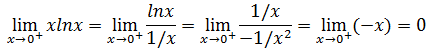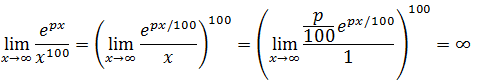数学笔记28——不定式和洛必达法则
我们已经能够处理很多极限,但是对于一些特殊情况的极限问题,过去的方法显得有些苍白。在先前内容的铺垫下,我们终于可以处理一些不定型的极限问题了,其中包括“0/0”型、“∞/∞”型,这一切都是通过“洛必达法则”实现的。从此,我们甚至能够判断“∞的大小”。
不定式
把某些型如0/0或∞/∞的极限成为型不定式。其它常见的不定式还有00、0·∞、∞0、1∞、∞-∞
例如![]() 是一个00型不定式,底数和指数是两股相反的力量,底数想让表达式极限趋近于0,指数想让表达式趋近于1,二者互相较劲,看谁的力量更胜一筹。
是一个00型不定式,底数和指数是两股相反的力量,底数想让表达式极限趋近于0,指数想让表达式趋近于1,二者互相较劲,看谁的力量更胜一筹。
洛必达法则
0/0型的极限
先来看一个例子:
这无法用直接代入的方法求解了,是一个典型的0/0型极限。可以试着用长除法解决:
虽然能够求得极限,但计算过程太过繁琐,下面尝试使用更简单的办法。
先将极限做一次变形:
如果令f(x) = x10 – 1,f(1) = 0,那么
这正是导数的定义。
同理,令g(x) = x2 – 1, g’(x) = 2x
公式
把上面的方法更系统化,就离洛必达法则更进一步了。
如果 ![]() 是0/0的极限,那么有f(a) = g(a) = 0,该极限的求解过程如下:
是0/0的极限,那么有f(a) = g(a) = 0,该极限的求解过程如下:
这就是洛必达法则:
上式成立的前提是:f(a) = g(a) = 0;等号右侧的极限存在。第二点有点微妙——右端的存在证明了左端的存在。
示例1
示例2
这一步仍未解决问题,还是0/0型,于是再次使用洛必达法则:
与线性逼近的比较
如果用线性逼近(线性逼近可参考数学笔记6——线性近似和二阶近似)计算上节的示例,则在x→0时:
利用二阶近似,在x→0时:
结果与使用洛必达法则计算的相等。
洛必达法则的推广
前面提到洛必达法则的基本定理:
上式成立的前提是:f(a) = g(a) = 0;等号右侧的极限存在。第二点有点微妙——右端的存在证明了左端的存在。
定理的推广
⑴ 该定理所有条件中,对a = ±∞的情况,结论依然成立。
⑵ 该定理第一条件中,对f(a)和g(a),极限皆为 ±∞的情况,结论依然成立。
简单地说,洛必达法则仅对0/0和∞/∞直接适用,其它构型需要经过一定的演算和变形,使其变为0/0或∞/∞。
示例1
0·(-∞)型像是两个式子在比赛,看谁的变化速度更快,但这不能直接使用洛必达法则,所以原式需要经过演化:
这次变成了(-∞/∞),即∞/∞型,可以直接使用洛必达法则:
当x→0+时,x的变化速度要快于lnx。
示例2
![]()
当x→∞时,x比epx变化的缓慢。
示例3
一个典型的∞/∞型,但是在使用洛必达法则时会遇到麻烦:
这并没有实质性的进展。当然,我们可以推算出,在经过连续使用洛必达法则后,分子依然趋近∞,分母最终将变成一个常数,所以最终结果是∞。
这个结果并不直观,我们尝试使用更直观的方式得出结论,这需要一点代数技巧。
由此可以得出这样的结论:指数函数的变化率胜过任何幂函数。
示例4
结论:对数函数比任何幂函数都变化的更慢。
示例5
这是00型,不能直接使用洛必达法则,所以仍需进行演化,这里的演化方式是使用e作为底数:
![]()
在示例1中得知,
注意事项
陷阱
0/0型可以直接使用洛必达法则,求导也很简单,因此很高兴的计算如下:
根据线性逼近重新计算一下:
得到了两个截然相反的结果,一定是其中某个环节出现了问题。在第一个计算中:
左边的式子是1/0型,不能使用洛必达法则!所以这个等式是错的。实际上可以直接得到左侧等于∞的结论。
不要忘记基础知识
∞/∞是符合洛必达法则的,但在这个例子中没有必要去使用洛必达法则。分子的最高次项是x5,分母是x4,所以分子是分母的高阶无穷,因此可以直接得出结论,结果是∞。
这个例子给我们的提示就是:不要忘记基础知识。
洛必达表法则不适用的情况
∞/∞型,使用洛必达法则:
看起来更复杂了。cosx的取值范围是[-1, 1],所以当x→∞时可以直接求得极限:
不要忘记基础知识。
综合示例
示例1
0/0型,
示例2
示例3
0/0型,
示例4
∞/∞型,