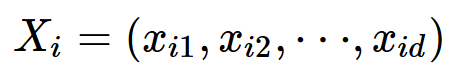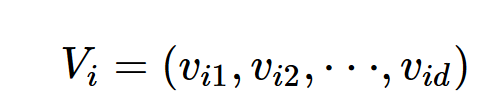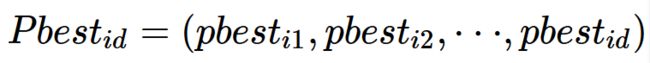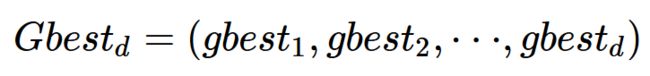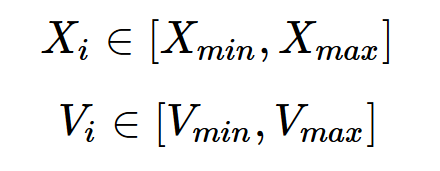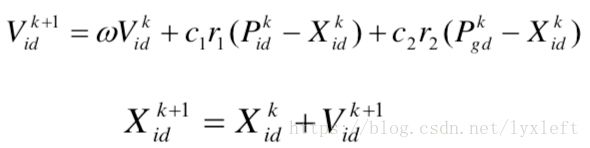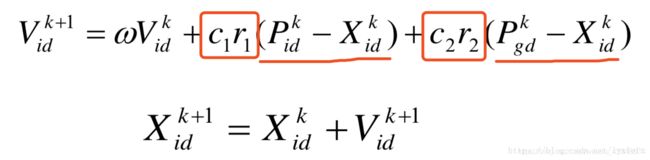数学建模——粒子群算法（POS）

注：本博客仅做个人学习参考使用，引用下述两篇优秀博客较多，且排版、解释有较大缺陷。推荐下列两篇博客学习粒子群算法

推荐博客：

https://www.cnblogs.com/Qling/p/9343625.html

https://blog.csdn.net/lyxleft/article/details/82978362

一、粒子群优化算法概述

粒子群优化(PSO, particle swarm optimization)算法是计算智能领域，除了蚁群算法，鱼群算法之外的一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究得到启发而想出来的。

鸟类捕食行为

鸟妈妈有7个鸟宝宝，有一天，鸟妈妈让鸟宝宝们自己去找虫子吃。于是鸟宝宝们开始了大范围的捕食行为。一开始鸟宝宝们不知道哪里可以找得到虫子，于是每个鸟宝宝都朝着不同的方向独自寻找。

但是为了能够更快的找到虫子吃，鸟宝宝们协商好，谁发现了虫子，就互相说一声。

找了一会，终于有一个鸟宝宝（称之为小蓝），似乎发现在他附近不远处有虫子的踪迹。于是它传话给其他鸟宝宝，其他鸟宝宝，收到消息后，边开始改变轨迹，飞到小蓝这边。最终，随着小蓝越来越接近虫子。其他虫宝宝也差不多都聚集到了小蓝这边。最终，大家都吃到了虫子。

故事分析

鸟宝宝捕食的故事，正是这个粒子群算法存在的原因。因此，如果想更好的了解粒子群算法，我们就要来分析鸟宝宝捕食的故事。首先，我们来分析分析鸟宝宝们的运动状态，即鸟宝宝自身是怎么决定自己的飞翔速度和位置的。

(1) 首先，我们知道物体是具有惯性的，鸟宝宝在一开始飞翔的时候，无论它下一次想怎么飞，往哪个方向飞，它都有一个惯性，它必须根据当前的速度和方向来进行下一步的调整。对吧，这个可以理解吧，因此，“惯性” ——当前的速度vcurrent 是一个因素。

(2) 其次，由于鸟宝宝长期捕食，因此鸟宝宝有经验，它虽然不知道具体哪里是有虫子的存在，但是它能大概知道虫子分布在哪里。比如当鸟宝宝飞到贫瘠的地方，它肯定知道这里是不会有虫子的，因此，在鸟宝宝的心中，它每次飞，都会根据自己的经验来找，比如以往虫子分布的地区，它肯定优先对这部分的地方进行搜索。因此，自己的“认知”——经验，也是一个因素。

(3) 最后，每个鸟宝宝发现自己离虫子更接近的时候，便会发出信号给同伴，在遇到这样的信号，其余还在找的鸟宝宝们就会想着，同伴的位置更接近虫子，我要往它那边过去看看。我们称之为“社会共享”，这也是鸟宝宝在移动时考虑的一个因素。

综上所述，鸟宝宝每次在决定下一步移动的速度和方向时，脑子里是由这三个因素影响的。我们想，如果能够用一条公式来描述着三个因素的影响的话，那不就能写出每个鸟宝宝的移动方向和速度么。但是，每一个鸟宝宝，对这三个因素的考虑都是不一致的，比如对于捕食经验不高的鸟宝宝，移动的时候会更看重同伴分享的信息，而对于捕食经验高的鸟宝宝，则更看重自己的经验。因此，我们的公式，在“认知”和“社会共享”这部分，是具有随机性的。

(1) 每一个鸟宝宝，都是我们的解，称之为“粒子”，而我们的虫子，就是我们问题的最优解。也就是说，鸟宝宝捕食过程，也就是所有的粒子在解空间内寻找到最优解的过程。

(2) 每一个粒子，都由一个fitness function来确定fitness value，以此来确定粒子位置的好坏。（这个其实就是模仿鸟宝宝的“经验”判断部分，通过fitness function来确定这个位置是不是所谓的贫瘠地或是虫子可能出现的位置）。

(3) 每一个粒子被赋予了记忆功能，能够记忆所搜寻过的最佳位置。

(4) 每一个粒子都有一个速度以及决定飞行的距离和方向，这个根据它本身的飞行经验和同伴共享的信息所决定。

算法公式

PSO算法首先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度值三项指标表示该粒子特征。

粒子i的位置：

粒子i的速度：

粒子i所搜寻到的最好的位置（personal best）：

种群所经历的最好的位置(global best)：

给我们的粒子速度和位置做一个限制，毕竟我们不希望鸟宝宝的速度过快或者以及飞出我们要搜寻的范围。因此对于每个粒子i，有：

核心步骤，参数更新

1. 粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置，个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置，群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。

2. 粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

在每一次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，更新公式如下:

在上式中，上标k-1和k表示粒子从k-1次飞行操作到下一次飞行操作的过程。

分别是我们前面分析的“惯性”、“认知”、“社会共享”这三大块

上式中V是速度，以当前的速度加上两个修正项：该个体与当前行进路径中最优个体的差距、与群体最优值的偏差。w是一个惯性的权重，是用于调节对解空间的搜索范围; c1和c2是系数，表示我们自己对给“认知”和“社会共享”这两部分的分量的控制; r1、r2是随机数, 给“认知”和“社会共享”提供随机性，即每个粒子对这两部分的看重是不一样的。。

X是位置，用当前位置加上速度。根据相邻时间间隔默认为一个时间单位，故速度和距离可以直接相加。

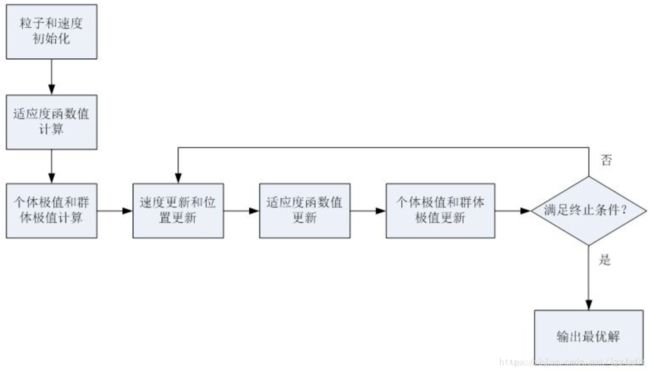
PSO算法步骤

　(1) Initial:

初始化粒子群体（群体规模为n），每个粒子的信息包括随机位置和随机速度。

(2) Evaluation

根据fitness function，算出每个粒子的fitness value。

(3) Find the Pbest

对于每个粒子，将其当前的fitness value与历史最佳的位置（Pbest）所对应的fitness value做比较。若当前的fitness value更高，则将当前的位置更新Pbest。

(4) Find the Gbest

对于每个粒子，将其当前的fitness value与群体历史最佳的位置（Gbest）所对应的fitness value做比较。若当前的fitness value更高，则将当前的位置更新Gbest。

(5) Update the Velocity and Position:

根据公式更新每个粒子的速度和位置

(6) 如果未找到最佳值，则返回步骤2。（若达到了最佳迭代数量或者最佳fitness value的增量小于给定的阈值，则停止算法）

步骤中的关键点提示：

1）初始化、适应度函数计算和遗传算法很相似。

2）群体极值是好找的。但个体极值：第一步时，每个个体的值都是个体极值，第二步后才开始有真正的个体极值的概念。

3）终止条件：比如说，达到多少次迭代次数，相邻两次误差小于一定值，等等。也可以多种终止条件混合使用。

PSO（粒子群优化算法）与GA（遗传算法）对比

• 相同点:

1）种群随机初始化，上面也提到了。

2）适应度函数值与目标最优解之间：都有一个映射关系

• 不同点:

1）PSO算法没有选择、交叉、变异等操作算子。取而代之的是个体极值、群体极值来实现逐步优化的功能。GA的相关操作含义参见《遗传算法原理简介及其MATLAB实践》。

2）PSO有记忆的功能：

在优化过程中参考到了上一步的极值情况（划横线的部分）。按此公式计算出新的粒子位置时，若新粒子的适应度函数还不如之前的好，则这个优化方法会帮助优化进程回到之前的位置，体现了一个记忆的效果。矩形内是权重系数。

3）信息共享机制不同，遗传算法是互相共享信息，整个种群的移动是比较均匀地向最优区域移动，而在PSO中，只有gBest或lBest给出信息给其他粒子，属于单向的信息流动，整个搜索更新过程是跟随当前最优解的过程。因此， 在一般情况下，PSO的收敛速度更快。

简单直白地理解：GA在变异过程中可能从比较好的情况又变成不好的情况，不是持续收敛的过程，所以耗时会更长些。

粒子群算法优点

1. 不依赖于问题信息，采用实数进行求解，算法具有较强的通用性

2. 原理简单，易于实现，需要调整的参数少

3. 收敛速度快，对计算机的内存要求不大

4. 粒子群算法所具有的飞跃性使得其更容易找到全局最优值，而不会被困在局部最优

PSO的MATLAB实现

MATLAB2014以上有自带的PSO的工具箱函数。

这里我们自己写代码来实现一下PSO：

【例】利用PSO寻找极值点：y = sin(10pix) / x;

%% I. 清空环境
clc
clear all
 
%% II. 绘制目标函数曲线图
x = 1:0.01:2;
y = sin(10*pi*x) ./ x;
figure
plot(x, y)
hold on
 
%% III. 参数初始化
c1 = 1.49445;
c2 = 1.49445;
 
maxgen = 50;   % 进化次数  
sizepop = 10;   %种群规模
 
Vmax = 0.5;   %速度的范围，超过则用边界值。
Vmin = -0.5;  
popmax = 2;   %个体的变化范围
popmin = 1;
 
%% IV. 产生初始粒子和速度
for i = 1:sizepop
    % 随机产生一个种群
    pop(i,:) = (rands(1) + 1) / 2 + 1;    %初始种群，rands产生(-1,1)，调整到(1,2)
    V(i,:) = 0.5 * rands(1);  %初始化速度
    % 计算适应度
    fitness(i) = fun(pop(i,:));   
end
 
%% V. 个体极值和群体极值
[bestfitness bestindex] = max(fitness);
zbest = pop(bestindex,:);   %全局最佳
gbest = pop;    %个体最佳
fitnessgbest = fitness;   %个体最佳适应度值
fitnesszbest = bestfitness;   %全局最佳适应度值
 
%% VI. 迭代寻优
for i = 1:maxgen
    
    for j = 1:sizepop
        % 速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax)) = Vmax;
        V(j,find(V(j,:)<Vmin)) = Vmin;
        
        % 种群更新
        pop(j,:) = pop(j,:) + V(j,:);
        pop(j,find(pop(j,:)>popmax)) = popmax;
        pop(j,find(pop(j,:)<popmin)) = popmin;
        
        % 适应度值更新
        fitness(j) = fun(pop(j,:)); 
    end
    
    for j = 1:sizepop    
        % 个体最优更新
        if fitness(j) > fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        % 群体最优更新
        if fitness(j) > fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end 
    yy(i) = fitnesszbest;          
end
 
%% VII. 输出结果并绘图
[fitnesszbest zbest]
plot(zbest, fitnesszbest,'r*')
 
figure
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

利用粒子群算法计算二元函数的最大值

%% 题目2： 利用粒子群算法计算二元函数的最大值
 
%% I. 清空环境
clc
clear
 
%% II. 绘制目标函数曲线
figure
[x, y] = meshgrid(-5: 0.1: 5, -5: 0.1: 5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
mesh(x,y,z)
hold on
 
 
%% III. 参数初始化
c1 = 1.49445;
c2 = 1.49445;
 
maxgen = 1000;                                                  % 进化次数 
sizepop = 100;                                                  % 种群规模
dimension = 2;                                                  % 这里因为是二元函数的求解，即二维，故列数为2
 
% 速度的边界
Vmax = 1;
Vmin = -1;
% 种群的边界
popmax = 5;
popmin = -5;
% 用于计算惯性权重，经验值
ws = 0.9;
we = 0.4;
 
% 给矩阵预分配内存
pop = zeros(sizepop, dimension);
V = zeros(sizepop, dimension);
fitness = zeros(sizepop, 1);
yy = zeros(maxgen);
w = zeros(maxgen);
%% IV. 产生初始粒子和速度
for i = 1: sizepop
    % 随机产生一个种群
    pop(i, :) = 5 * rands(1, 2);                                % 初始种群
    V(i, :) = rands(1, 2);                                      % 初始化速度
    % 计算适应度
    fitness(i) = fun(pop(i, :));
end
 
%% V. 初始化Personal best和Global best
[bestfitness, bestindex] = max(fitness);
gbest = pop(bestindex, :);                                      % Global best
pbest = pop;                                                    % 个体最佳
fitnesspbest = fitness;                                         % 个体最佳适应度值
fitnessgbest = bestfitness;                                     % 全局最佳适应度值
 
%% VI. 迭代寻优
for i = 1: maxgen
    w(i) = ws - (ws - we) * (i / maxgen);                       % 让惯性权重随着迭代次数而动态改变，控制搜索精度   
    for j = 1: sizepop
        % 速度更新
        V(j, :) = w(i)*V(j, :) + c1*rand*(pbest(j, :) - pop(j, :)) + c2*rand*(gbest - pop(j, :));
        for k = 1: dimension
            if V(j, k) > Vmax
                V(j, k) = Vmax;
            end
            if V(j, k) < Vmin
                    V(j, k) = Vmin;
            end
        end
         
        % 种群更新(位置更新)
        pop(j, :) = pop(j, :) + V(j, :);
        for k = 1: dimension
            if pop(j, k) > popmax
                pop(j, k) = popmax;
            end
            if pop(j, k) < popmin
                pop(j, k) = popmin;
            end
        end
        % 适应度值更新
        fitness(j) = fun(pop(j, :));
    end
     
    for j = 1: sizepop   
        % 个体最优更新
        if fitness(j) > fitnesspbest(j)
            pbest(j, :) = pop(j, :);
            fitnesspbest(j) = fitness(j);
        end
         
        %群体最优更新
        if fitness(j) > fitnessgbest
            gbest = pop(j, :);
            fitnessgbest = fitness(j);
        end
    end
    yy(i) = fitnessgbest;                                           % 记录每次迭代完毕的群体最优解
end
%% VII.输出结果
[fitnessgbest, gbest]
plot3(gbest(1), gbest(2), fitnessgbest, 'bo','linewidth', 1.5)
 
figure
plot(yy)
title('最优个体适应度', 'fontsize', 12);
xlabel('进化代数', 'fontsize', 12);
ylabel('适应度', 'fontsize', 12);

其中，适应值函数被封装到fun.m中，如下：

function y = fun(x)
%函数用于计算粒子适应度值
%x           input           输入粒子
%y           output          粒子适应度值
y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

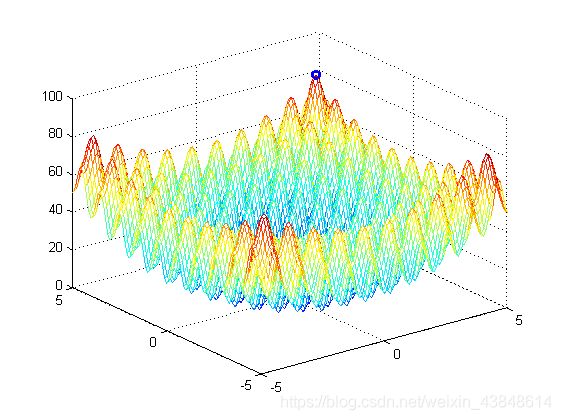
运行上述代码，得到的数据和图如下：

ans =
   80.7066    4.5230    4.5230

可以看到，图中标注的地方是我们求得的最大值处。其实我们知道，对于这个函数，因为是对称的，所以4个点都是同样的最大值，这就是粒子群算法的缺点了。很容易陷入局部最优解。因为我们的粒子群算法其实并不知道什么是最优解，它只是让粒子不断的找一个相对之前所有的解都是最好的一个解。所以，这样的粒子群算法是有局限性的，用的时候要根据场合来选择。