神经网络训练技巧讨论：为什么需要标准化

本文关注：对于神经网络（主要是全连接网络+SGD）的学习训练，标准化有什么好处（加速收敛），以及为什么有这样的好处。本文观点大多总结自lecun98年的论文：Efficient BackProp，详情请参考原论文。翻译以及总结过程如有疏漏，欢迎指教。另需说明的是：神经网络模型多变复杂，这里多是对于一般情况的启发性讨论，实际使用中需要具体情况具体分析（例如图像领域大多仅减均值，不除方差）。

---

什么是标准化

在机器学习领域中，标准化(standardization)是预处理（preprocessing）的常见步骤之一。其操作为减均值除方差，生成的分布均值为0方差为1，其公式为：

xi=xi−μiδi(μi=∑Nj=1x(j)iN, δ2i=∑Ni=1(x(j)i−μi)2N−1) x i = x i − μ i δ i ( μ i = ∑ j = 1 N x i ( j ) N ,   δ i 2 = ∑ i = 1 N ( x i ( j ) − μ i ) 2 N − 1 )

其中 xi x i 表示输入 x x 的第 i i 维， x(j)i x i ( j ) 表示训练集中第 j j 个样本的第 i i 维的值，训练集中总共有 N N 个样本， μi,δi μ i , δ i 为训练集预估的第 i i 维的均值和方差。

为什么需要标准化

简要地说，为了保证网络可以良好的收敛，在不清楚各个维度的相对重要程度之前，标准化使得输入的各个维度分布相近，从而允许我们在网络训练过程中，对各个维度“一视同仁”（即设置相同的学习率、正则项系数、权重初始化、以及激活函数）。反过来，当我们使用全局相同的学习率、权重初始化、以及激活函数等网络设置时，方差更大的维度将获得更多的重视。

网络设置, BP, SGD简介

具体地，考虑单层全连接网络的情况

y=Wx+b⇔yi=∑j=1nwijxj+bi=wTix+b y = W x + b ⇔ y i = ∑ j = 1 n w i j x j + b i = w i T x + b

，SGD等基于BP一阶梯度的优化算法的常见形式为

∂L∂W=∂L∂yxT⇔∂L∂wi=∂L∂yixW=W−η∂L∂W=W−η∂L∂yxT⇔wi=wi−η∂L∂wi=wi−η∂L∂yix ∂ L ∂ W = ∂ L ∂ y x T ⇔ ∂ L ∂ w i = ∂ L ∂ y i x W = W − η ∂ L ∂ W = W − η ∂ L ∂ y x T ⇔ w i = w i − η ∂ L ∂ w i = w i − η ∂ L ∂ y i x

其中 wi w i 为参数矩阵 W W 的第 i i 行元素组成的向量（即第 i i 行的转置）， xi,yi x i , y i 分别为输入 x x 输出 y y 的第 i i 维元素值， η η 为学习率， L L 为损失函数。

注意到 η η 以及 ∂L∂yi ∂ L ∂ y i 均为标量，故 wi w i 的收敛方向仅由 x x 决定。Moreover，因为 η η 和 ∂L∂yi ∂ L ∂ y i 对各维相同，故 wi w i 各维的相对收敛速度仅由 x x 决定。举例说明，若输入永远是正值，即 x(j)>0, ∀j=1⋯N x ( j ) > 0 ,   ∀ j = 1 ⋯ N ，则 wi w i 每一步收敛的方向均在第一或第三象限（因为 ∂L∂wi ∂ L ∂ w i 各维符号相同）；若输入第一维的值永远是第二维的00倍，即 x(j)1=100x(j)2, ∀j=1⋯N x 1 ( j ) = 100 x 2 ( j ) ,   ∀ j = 1 ⋯ N ，则 wi1 w i 1 每次收敛的步长都是 wi2 w i 2 的100倍。可以发现，当学习率相同时， Δwi Δ w i 与 x x 的分布直接相关，这也是输入分布影响收敛速度的原因。

减均值的优点

再次考虑上诉极端例子：若输入永远是正值，即 x(j)>0, ∀j=1⋯N x ( j ) > 0 ,   ∀ j = 1 ⋯ N ，则 wi w i 每一步收敛的方向均在第一或第三象限（因为 ∂L∂wi ∂ L ∂ w i 各维符号相同）。收敛过程中，权值只能走z字形的路线收敛，从而收敛缓慢，没有效率。如下图所示：

通常情况下，任意方向的均值偏移均会使得梯度值在某一方向产生偏移，从而减缓学习过程。所以常见的鲁棒性做法是将数据集平移至均值为0，此启发式观点对任意层输入有效（详见BatchNorm的ICS）。

除方差的优点

首先feature scaling相关方法（包括标准化，归一化等）都具有的好处是消除量纲，即减少数据表征方式对模型结果的影响。

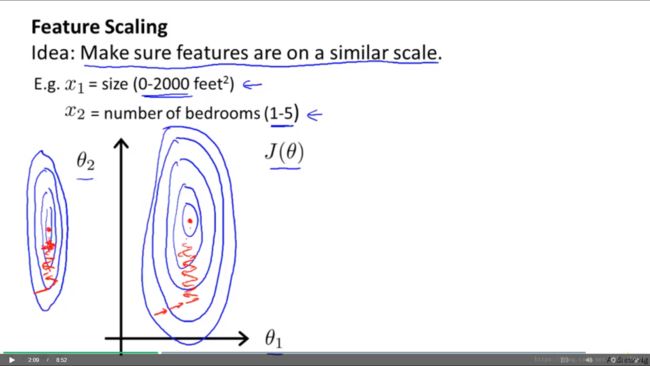
其次，因为学习率等网络设置对全局相同，我们往往期待损失曲面越spherical越好（即各方向的增减趋势幅值相近）；一种未知先验的鲁棒性假设是各维重要程度相同，从而将各维尺度伸缩至一致的情况下损失曲面最spherical；反过来，原本spherical的损失曲面，若对某一维进行拉伸，新的loss contour会更加的skinny，如下图所示（截屏自Andrew NG的coursera课程）

权重在skinny的loss contour收敛时，学习率的最大值受最大尺度限制（对于多项式曲面，理论上不超过最优学习率的2倍），在尺度较小方向的收敛速度会远小于最优值，从而收敛缓慢（此种简单情况可以通过momentum减弱其影响）。同时若各维度的重要程度相似，因为学习率的调节更多关注大尺度维度的收敛效果，可知输入维度的尺度（variance）越大其受重视程度越大，收敛效果越好。

另需说明方差为1不是唯一的做法，输入方差的选择是与学习率+激活函数+权重初始化方式联动的。我们往往希望激活函数的输入分布在激活函数有效区间内（对于tanh等sigmoid类函数，即不能过小，也不能过大，过小会丧失非线性，过大会梯度消失），而激活函数的输入由网络层输入和权重共同决定。标准化至方差为1是学术界常见的做法，以此为基础提出的权重初始化（Xavier, He）以及激活函数（ELU, tanh）有许多成熟方案/参数可以借鉴，因此未知先验的情况下常常进行方差为1的标准化。

除方差的缺点

如上所述，除方差将输入各维的尺度统一，内涵假设是各维输入重要程度相近。但若实际情况下，某一维为不相干弱噪声，除方差会加大噪声对模型的影响（此影响在白化过的输入中更明显）。同时，若已知各维输入量纲相近，或已知各维相对重要程度的情况下，往往选择保留输入的相对尺度，对各维统一缩放。

---

参考资料：
[1] LeCun, Yann A., et al. “Efficient backprop.” Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012. 9-48.
[2] http://cs231n.stanford.edu/
[3] https://www.coursera.org/learn/machine-learning/home/welcome