“科林明伦杯” 哈工大第十届程序设计竞赛【B&C&D&E&F&H&J签到】

问题B. 减成一
题目描述
存在n个数，每次操作可以任选一个区间使得区间内的所有数字减一。问最少多少次操作，可以让所有数都变成1。
数据保证一定有解。

输入描述:
输入t，代表有t组数据。每组数据输入n，代表有n个数。接下来一行输入n个数，数字大小小于1e6。(t<=1000，n<1e5，∑n < 1e6)

输出描述:
每组数据输出一个整数代表最少需要操作的次数。

输入
1
6
1 3 5 2 7 1

输出
9

题解： 先贴一下官方题解


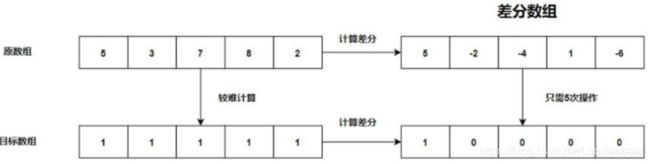
再说一说更简单直接的方法：直接模拟，手写几组数据，我们不难发现：下标从1开始输入数组元素a[i]，定义一个a[0]=1，结果就是这一数列中相邻的在后边的大数减前边小数之差的和。

//#pragma GCC optimize(3,"Ofast","inline")
#include  
using namespace std; 
const int N=1e5+10;
typedef long long LL;
 
int T,a[N];
 
int main()
{
    cin>>T;
    while(T--)
    {
        int n;
        cin>>n;
        LL sum=0;
        a[0]=1;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            if(a[i]>a[i-1]) sum+=a[i]-a[i-1];
        }
        cout<< sum <<endl;
    }
    return 0;
}

问题C. 面积
题目描述
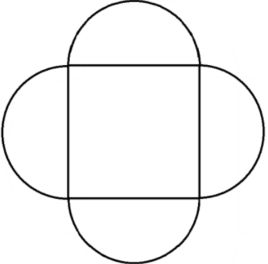
如图所示，正方形周围接4个半圆，求图形的面积

输入描述:
输入t，代表有t组数据。每组数据输入正整数x，代表正方形的边长。(t<100, x<1000)

输出描述:
输出图形面积，并保留2位小数，其中π取3.14。

输入
1
1

输出
2.57

题解：水题，注意数据类型、控制精度。

#include 
#define ll long long 
using namespace std;

ll t,a;
int main()
{
	cin>>t;
	while(t--){
		cin>>a;
		double x=a/2.0;
		double s=a*a+3.14*x*x*2;
		printf("%.2lf",s);
		cout<<endl;
	}
	return 0;
}

问题D. ren硬币
题目描述
有n枚硬币，每枚硬币扔出来是正面和反面的概率各占50%。小明同时扔下了n枚硬币后，已知至少有m枚硬币是反面。请问恰好有k枚硬币是正面的概率是多少。

输入描述:
输入t，代表有t组数据。每组数据输入一个数n，m，k，代表有n枚硬币，抛出以后至少有m枚是反面的情况下，恰好有k个正面的概率。(t<=1000，n<1e5，m<=1000，k<=n)

输出描述:
对于结果是p/q，输出分数取模1e9+7后的结果。

输入
1
10 3 5

输出
797520667

#include 
using namespace std;
typedef long long ll;
const int MAXN = 1e5+7;
const int mod = 1e9+7;
 
ll q_pow(ll a, ll b, ll mod) { // 快速幂
    ll res = 1LL;
    while (b) {
        if (b&1)  res = (res*a) % mod;
        a = (a*a) % mod;
        b >>= 1;
    }
    return res % mod;
}
 
ll inv(ll x) {
    return q_pow(x, mod-2, mod);
}
 
ll factorial[MAXN] = { 1 }; // 阶乘
 
inline ll C(ll n, ll k) {
    return factorial[n] * inv(factorial[n-k] * factorial[k]%mod) % mod;
}
 
int main() {
    std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    
    factorial[0] = 1;
    for(int i=1; i<=MAXN-7; ++i)
        factorial[i] = factorial[i-1]*i % mod;
        
    int t;  
	cin>>t;
    while (t--) {
        ll n,m,k;    
		cin>>n>>m>>k;
        if(k+m > n) {
            cout<<0<<endl;
            continue;
        }
        ll a=C(n,k), b=q_pow(2,n,mod);
        for(int i=0; i<m; ++i)
            b = (b-C(n,i)+mod) % mod;
        cout<< a*inv(b) % mod <<endl;
    }
}

问题E. 赛马
题目描述
一天小明与他同学准备赛马，他们每人有n匹马，每匹马有一个固定的战力值，战力值高的马会战胜战力值低的马并赢得比赛。每匹马只能出场比赛一次。小明偷看到了他对手每匹马的出场顺序，小明在更改自己马出场顺序后最多能赢多少场比赛。

输入描述:
输入t，代表有t组数据。每组数据输入正整数n，每人的马匹数量。下一行输入n个值a[i]，代表小明每匹马的战力值。接下来一行输入n个值b[i]，代表对手按顺序出场的每匹马的战力值。(t<=10, n<1000，1<=i<=n，a[i]<1e6，b[i]<1e6)

输出描述:
小明在更改马匹出场顺序后，最多能赢的场数。

输入
1
3
5 8 8
4 7 10

输出
2

题解：分别升序sort两个数组，想象两个指针，初始时分别指向a、b数组的首个元素，若满足a[1]>b[1]，两个指针分别后移，否则指向数组a的元素的指针后移，直到找到当前花最小代价就能胜利的，以此类推，这样就能够实现胜利次数最大化。

//#pragma GCC optimize(3,"Ofast","inline")
#include 
#define ll long long 
using namespace std;
ll a[10000],b[10000],cnt,t,n;

int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        for(int i=1;i<=n;i++) cin>>a[i];
        for(int i=1;i<=n;i++) cin>>b[i];
 
        cnt=0;
        sort(a+1,a+1+n);
        sort(b+1,b+1+n);
        
        for(int i=1,j=1;i<=n;)
		{
            if(a[i]>b[j])    i++, j++, cnt++;
            else i++;
        }
        cout<<cnt<<endl;
    }
    return 0;
}

问题F. 三角形
题目描述
小明有一根长度为a的木棒，现在小明想将木棒分为多段（每段木棒长度必须为整数），
使得分隔后的木棍中，取出的任意三段都不能构成三角形，小明想知道木棒最多被分成几段？

输入描述:
输入数据的第一行是t，表示数据的组数, 接下来每组数据输入一个a（t<=1000, 1 <= a < 2^64 - 1）

输出描述:
对于每组输入样例，打印木棒最多被分为多少段

输入
2
1
3

输出
1
2

题解：不用多说了，上官方题解：

#include 
using namespace std;
typedef unsigned long long ull;
ull f[101];
 
void fun()
{
    f[1]=1,f[2]=1;
    for(int i=3;i<=101;i++)
        f[i]=f[i-1]+f[i-2];
}
 
int main() {
    std::ios::sync_with_stdio(0),cin.tie(0);
    int t;
    cin>>t;
    fun();
    while(t--) {
        ull n;
        cin>>n;
        ull i=1,cnt=0;
        while(1) {  
            if(n<f[i]) break;
            n-=f[i];
            cnt++;
            i++;
        }
        cout<<cnt<<endl;
    }
    return 0;
}

问题H. 直线
题目描述
平面上存在n条直线。请问n条直线在平面上最多存在多少交点。

输入描述:
输入数据的第一行是t，表示数据的组数（t < 100）, 接下来每组数据输入一个n（1<=n <= 1e15）

输出描述:
对于每组输入样例，打印n条直线最多有多少个交点

输入
2
1
2

输出
0
1

题解：n条直线在平面上最多存在 n (n-1)/2 个交点，但这题数据太大，超ll了。一般数字比较大的题，要么高精、要么字符数组、要么黑科技，这里选择了第三者——__int128。

/*
    __int128 不能使用 cin，cout，要定义 print函数
    【补充一句有关 cin和 cout，尽量别用，如果非要用，就加上  
      std::ios::sync_with_stdio(false);
      cin.tie(0);
      cout.tie(0);    来提升效率】
    __int128 在编译器上不支持，但 oj的在线测试能支持
*/

// __int128版
#include
using namespace std;

void print(__int128 x) {
    if(x>9)  print(x/10);
    putchar(x%10 +'0');
}

int main() {
    int t;
    cin>>t;
    __int128 n;
    while(t--) {
        scanf("%lld",&n);
        print(n*(n-1)/2);
        printf("\n"); // <=> puts("");
    }
    // system("pause"); 作用:冻结屏幕直到按任意键以继续
    return 0;
}

/*
// 数组版 
#include 
int main()
{
    int t;
    long long i,j,n,x,num[32],k,array;
    scanf("%d",&t);
    for(i=0;i0&&j==k-1)   k++;
        }
            
        for(j=k-1;j>=0;j--)
           printf("%d",num[j]);
        printf("\n");
    } 
    return 0;
}
*/

问题J. 最大值
题目描述
有一个字符串s，对于字符串中一个非前缀子串恰好为字符串的前缀我们称之为ac串。
请问给出一个字符串他的ac串最大长度为多少

输入描述:
输入数据第一行是t，表示数据的组数，接下来每组数据输入一个字符串s（t<=10，s<=1e5）

输出描述:
输出最大长度

输入
2
aaaaa
abacc

输出
4
1

说明
aaaab的ac串是aaa(2:4)
acac的ac串是ac(3:4)

题解：ac串——kmp中的next数组，即求字符串的next数组。

//#pragma GCC optimize(3,"Ofast","inline")
#include 
using namespace std;
string s;

int main(){
    int T;
	cin>>T;
    while(T--){
        cin>>s;
        int ans=0,flag=0;
        int len=s.size();
        
        for(int i=1;i<len;i++) {
            if(s[i]!=s[0]) continue;
            for(int j=ans+1;j<=len-i;j++) {
            //枚举ac串的最大长度  从小开始 从1 不行 从ans+1看有没有更大的
                if(s.substr(0,j)==s.substr(i,j)) {
                    ans=max(j,ans);
                    // flag=1;
                }
                else break;  //不匹配就不往下看了
            }
            // if(flag) break;
        }
        cout<<ans<<endl;
    }
}
 
/*
4
abbaba
ababc
abababc
abababa
 
1
acajacaj
**/