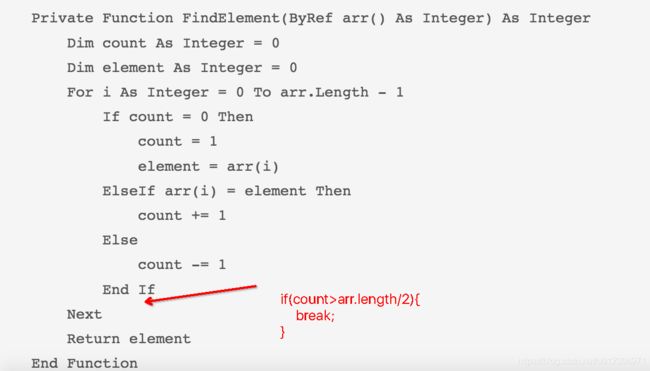
谁是众数

今天的算法题目是：

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

Input: [3,2,3]
Output: 3
Example 2:

Input: [2,2,1,1,1,2,2]
Output: 2

那么如何设计出高效的算法呢？你如果没有想到时间复杂度为N的算法，那么别费劲了直接参考一下答案吧。

答案：

逆向思考：

1、答案的思路是什么？

   这里众数的个数大于数组的一半，在这种众数占有绝对优势的情况下，其实全局来看其实问题就设计到了两个数：是众数、不是众数。所以呢，我们就拿众数跟非众数一个一个得相抵消。最终剩下的仍然是众数，更何况每次进行相邻数据相抵的时候还存在两个不同非众数的相抵。所以只需要O（N）就把众数找到了。

2、这里面很巧妙的地方在哪里？

众数占绝对优势。

这里面有个思考非常常用，就是用相抵的办法去等同地降低问题复杂度。这个思路在以后还会用到。

3、为什么你没想到答案？

正向思维太强，缺乏一定的逆向思维。

缺少这方面的训练。

4、学到了什么

 降维思想：问题等价地减少复杂度，这就要求洞察问题深刻，建模能力强。