图python(数据结构与算法)-----最小生成树
连通图:在无向图中,若从顶点v到顶点v'有路径,则称v和v'是连通的,若在改图中的任意两个顶点之间都是连通的,则称其为连通图。
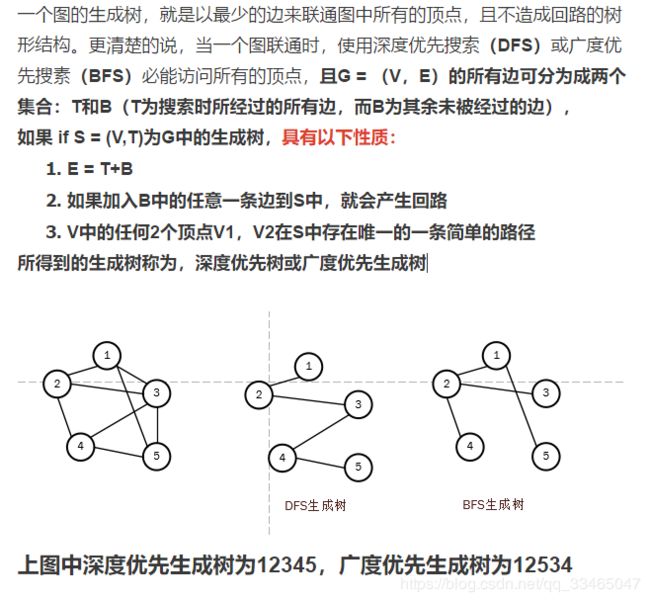
生成树
某一个具有n个顶点的连通图的生成树是该图的极小连通子图,生成树包含这一连通图中的n个顶点和n-1条边。
连通图的生成树是图的极小连通子图,它包含了图中的全部顶点,一个只有n个顶点的连通图的生成树只有n-1条边,若有n个顶点而少于n-1条边,则为非连通图,若多余N-1条边,则一定形成回路。
最小生成树:
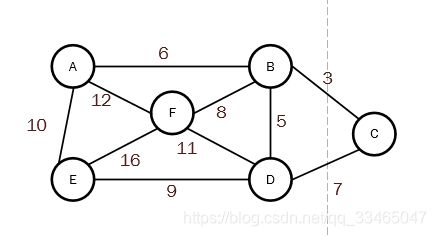
通常把各边带权的连通图称为连通网,在某一连通网的所有生成树种,对每一颗生成树的各边权重值求和,并找出权值和最小的生成树,这一生成树被称为连通网的最小生成树。产生最小生成树的算法:kruska算法和Prim算法。
最小生成树不唯一,满足以下3条准则:
- 只能使用图中的边构造最小生成树
- 具有n个顶点和n-1条边
- 不能使用产生回路的边
Prim算法:
(1)两个顶点之间的距离:将顶点u邻接到顶点的v的关联边的权值,记为|u,v|,若两个顶点之间不相连,则这两个顶点之间的距离为无穷大。
(2)顶点到顶点集合的距离:顶点到顶点集合中所有顶点的距离的最小值,记为|u,V|=min|u,v| ,
(3) 两个顶点集合之间的距离:顶点集合U的顶点到顶点集合V的距离的最小值,记为|U,V| = min|u,V|。
设图T是由n个顶点组成的连通无向图,是图G的最小生成树,其中V是T的顶点集,TE是T的边集,构造最小生成树的步骤为:
从源点开始,必存在一条边,使得U,V之间的距离最小,将加入到集合TE中,同时将顶点加入到顶点集中,直到U=V为止。
Kruskal算法
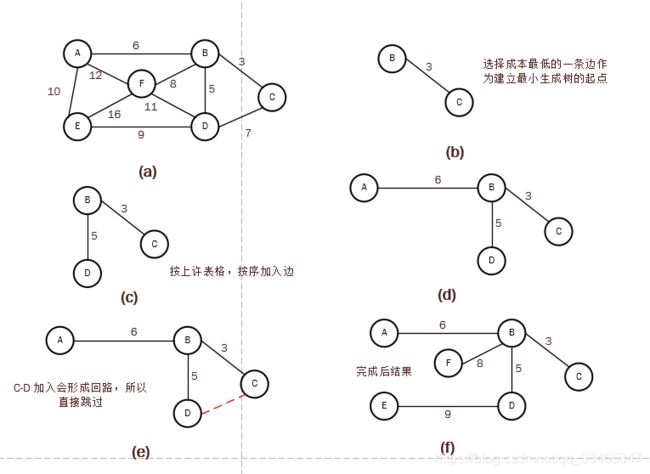
该算法是将各边的按权值大小从小到大排序,接着从权值最低的边开始建立最小成本生成树,如果假如边会造成回路,就舍弃不用,直到加入n-1个边为止。
步骤1:
| 起始顶点 |
终止顶点 |
成本 |
| B |
C |
3 |
| B |
D |
5 |
| A |
B |
6 |
| C |
D |
7 |
| B |
F |
8 |
| D |
E |
9 |
| A |
E |
10 |
| D |
F |
11 |
| A |
F |
12 |
| E |
F |
16 |
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 08:50:56 2019
@author: dell
"""
#coding=utf-8
class Graph(object):
def __init__(self, maps):
self.maps = maps
self.nodenum = self.get_nodenum()
self.edgenum = self.get_edgenum()
def get_nodenum(self):
return len(self.maps)
def get_edgenum(self):
count = 0
for i in range(self.nodenum):
for j in range(i):
if self.maps[i][j] > 0 and self.maps[i][j] < 9999:
count += 1
return count
def kruskal(self):
res = []
if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
return res
edge_list = []
for i in range(self.nodenum):
for j in range(i,self.nodenum):
if self.maps[i][j] < 9999:
edge_list.append([i, j, self.maps[i][j]])#按[begin, end, weight]形式加入
edge_list.sort(key=lambda a:a[2])#已经排好序的边集合
group = [[i] for i in range(self.nodenum)]
for edge in edge_list:
for i in range(len(group)):
if edge[0] in group[i]:
m = i
if edge[1] in group[i]:
n = i
if m != n:
res.append(edge)
group[m] = group[m] + group[n]
group[n] = []
return res
def prim(self):
res = []
if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
return res
res = []
seleted_node = [0]
candidate_node = [i for i in range(1, self.nodenum)]
while len(candidate_node) > 0:
begin, end, minweight = 0, 0, 9999
for i in seleted_node:
for j in candidate_node:
if self.maps[i][j] < minweight:
minweight = self.maps[i][j]
begin = i
end = j
res.append([begin, end, minweight])
seleted_node.append(end)
candidate_node.remove(end)
return res
max_value = 9999
row0 = [0,7,max_value,max_value,max_value,5]
row1 = [7,0,9,max_value,3,max_value]
row2 = [max_value,9,0,6,max_value,max_value]
row3 = [max_value,max_value,6,0,8,10]
row4 = [max_value,3,max_value,8,0,4]
row5 = [5,max_value,max_value,10,4,0]
maps = [row0, row1, row2,row3, row4, row5]
graph = Graph(maps)
print('邻接矩阵为\n%s'%graph.maps)
print('节点数据为%d,边数为%d\n'%(graph.nodenum, graph.edgenum))
print('------最小生成树kruskal算法------')
print(graph.kruskal())
print('------最小生成树prim算法')
print(graph.prim())结果:
邻接矩阵为
[[0, 7, 9999, 9999, 9999, 5], [7, 0, 9, 9999, 3, 9999], [9999, 9, 0, 6, 9999, 9999], [9999, 9999, 6, 0, 8, 10], [9999, 3, 9999, 8, 0, 4], [5, 9999, 9999, 10, 4, 0]]
节点数据为6,边数为8
------最小生成树kruskal算法------
[[1, 4, 3], [4, 5, 4], [0, 5, 5], [2, 3, 6], [3, 4, 8]]
------最小生成树prim算法
[[0, 5, 5], [5, 4, 4], [4, 1, 3], [4, 3, 8], [3, 2, 6]]