笔试考点整理---搜索问题整理
原题连接https://www.nowcoder.com/profile/242565499/myFollowings/detail/13266418
现有一个 3x3 规格的 Android 智能手机锁屏程序和两个正整数 m 和 n ,请计算出使用最少m 个键和最多 n个键可以解锁该屏幕的所有有效模式总数。
其中有效模式是指:
1、每个模式必须连接至少m个键和最多n个键;
2、所有的键都必须是不同的;
3、如果在模式中连接两个连续键的行通过任何其他键,则其他键必须在模式中选择,不允许跳过非选择键(如图);
4、顺序相关,单键有效(这里可能跟部分手机不同)。
输入:m,n
代表允许解锁的最少m个键和最多n个键
输出:满足m和n个键数的所有有效模式的总数
m,n =map(int, input().split(','))
visit=[False]*10
visit[0]=True
hash_=[[0]*10 for _ in range(10)]
hash_[1][3]=hash_[3][1]=2
hash_[1][7]=hash_[7][1]=4
hash_[9][3]=hash_[3][9]=6
hash_[7][9]=hash_[9][7]=8
hash_[1][9]=hash_[3][7]=hash_[2][8]=hash_[4][6]=5
hash_[9][1]=hash_[7][3]=hash_[8][2]=hash_[6][4]=5
def helper(m,n,index,num,visit,hash_):
res=0
if index>=m:
res+=1
if index+1>n:
return res
visit[num]=True
for i in range(1,10):
if visit[i]==False and visit[hash_[num][i]]==True:
res+=helper(m,n,index+1,i,visit,hash_)
visit[num]=False
return res
if n<=0 or m>n:
print(0)
else:
result=4*helper(m,n,1,1,visit,hash_)+4*helper(m,n,1,2,visit,hash_)+helper(m,n,1,5,visit,hash_)
print(result)
第二题
链接:https://www.nowcoder.com/questionTerminal/a788d1b9c9984e91ae5cdef32b8fcb5d
来源:牛客网
二阶魔方又叫小魔方,是222的立方形结构。每一面都有4个块,共有24个块。每次操作可以将任意一面逆时针或者顺时针旋转90°,如将上面逆时针旋转90°操作如下。
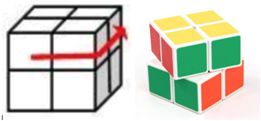
Nero在小魔方上做了一些改动,用数字替换每个块上面的颜色,称之为数字魔方。魔方上每一面的优美度就是这个面上4个数字的乘积,而魔方的总优美度就是6个面优美度总和。
现在Nero有一个数字魔方,他想知道这个魔方在操作不超过5次的前提下能达到的最大优美度是多少。
魔方展开后每一块的序号如下图:
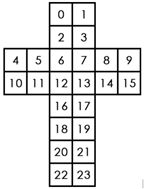
输入描述:
输入一行包含24个数字,按序号顺序给出魔方每一块上面的数字。所有数大小范围为[-100,100]。
输出描述:
输出一行包含一个数字,表示最大优美度。
示例1
输入
2 -3 -2 3 7 -6 -6 -7 9 -5 -9 -3 -2 1 4 -9 -1 -10 -5 -5 -10 -4 8 2
输出
8281
data=[int(x) for x in input().split()]
def M(data): #优美度计算
result=data[0]*data[2]*data[1]*data[3]
result+=data[4]*data[5]*data[10]*data[11]
result+=data[6]*data[7]*data[12]*data[13]
result+=data[8]*data[9]*data[14]*data[15]
result+=data[16]*data[17]*data[18]*data[19]
result+=data[20]*data[21]*data[22]*data[23]
return result
def op_1_1(data):
data_=data.copy() #操作要保留原来的data及当前状态,在当前状态向6种旋转尝试
data_[0]=data[10]
data_[1]=data[4]
data_[10]=data[19]
data_[4]=data[18]
data_[19]=data[9]
data_[18]=data[15]
data_[9]=data[0]
data_[15]=data[1]
data_[23]=data[22]
data_[22]=data[20]
data_[20]=data[21]
data_[21]=data[23]
return data_
def op_1_2(data):
data_=data.copy()
data_[2]=data[11]
data_[3]=data[5]
data_[11]=data[17]
data_[5]=data[16]
data_[17]=data[8]
data_[16]=data[14]
data_[8]=data[2]
data_[14]=data[3]
data_[6]=data[12]
data_[12]=data[13]
data_[13]=data[7]
data_[7]=data[6]
return data_
def op_2_1(data):
data_=data.copy()
data_[1]=data[7]
data_[3]=data[13]
data_[7]=data[17]
data_[13]=data[19]
data_[17]=data[21]
data_[19]=data[23]
data_[21]=data[1]
data_[23]=data[3]
data_[8]=data[14]
data_[14]=data[15]
data_[15]=data[9]
data_[9]=data[8]
return data_
def op_2_2(data):
data_=data.copy()
data_[0]=data[6]
data_[2]=data[12]
data_[6]=data[16]
data_[12]=data[18]
data_[16]=data[20]
data_[18]=data[22]
data_[20]=data[0]
data_[22]=data[2]
data_[5]=data[11]
data_[11]=data[10]
data_[10]=data[4]
data_[4]=data[5]
return data_
def op_3_1(data):
data_=data.copy()
data_[4]=data[6]
data_[5]=data[7]
data_[6]=data[8]
data_[7]=data[9]
data_[8]=data[23]
data_[9]=data[22]
data_[23]=data[4]
data_[22]=data[5]
data_[2]=data[3]
data_[3]=data[1]
data_[1]=data[0]
data_[0]=data[2]
return data_
def op_3_2(data):
data_=data.copy()
data_[10]=data[12]
data_[11]=data[13]
data_[12]=data[14]
data_[13]=data[15]
data_[14]=data[21]
data_[15]=data[20]
data_[21]=data[10]
data_[20]=data[11]
data_[16]=data[17]
data_[17]=data[19]
data_[19]=data[18]
data_[18]=data[16]
return data_
def helper(data,index,max_):#深度优先遍历
#print(max_)
M_=M(data)
if M_>max_:
max_=M_
if index==5:
return max_
for op in [op_1_1,op_1_2,op_2_1,op_2_2,op_3_1,op_3_2]:#宽度比较
M_=helper(op(data),index+1,max_)
if M_>max_:
max_=M_
return max_ #宽度比较完返回
print(helper(data,0,0))
