梯度下降 Gradient Descent 从二元到多元

机器学习

首先可以理解机器学习是从一个模型中找到最佳模型，模型是指一系列函数的集合。例如：y=k*x +b，这就是一系列线性函数的集合。

梯度下降（Gradient Descent）

梯度下降就是寻找最佳模型或者函数的方法之一，概念不多说，直接用实例解释更靠谱！（根据斜率的变化分布，调整lr很关键）

待求解问题：

有一组样本，请预测下一个值是多少？(数据y_data是某谣言每日增长量的案例值，单位：万条)
x_data=[0,1,2,3,4,5,6,7,8,9]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]

实例一：线性模型预测结果

设数据符合线性模型：y=ux + w，只需找到最合适的u与w即可。
这里要提到 Loss(f) 函数，就是计算某个函数的误差多少的函数，利用十个样本点带入y=ux + w，分别得出的十个y值与真实的y_data的差值。为了方便计算取平方
Loss(u,w)=∑ (y_data[n] - ( u*x_data[n]+w))^2
说明：∑是求1-10个样本点的差值平方和;n∈(1-10)
所以只需求得Loss(u,w)函数的最小值时的u与w即可！

import numpy as np
import matplotlib.pyplot as plt
x_data=[x for x in range(10)]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]

#u与w随便给出初始值
u= 2
w= -1
plt.plot(x_data,y_data)

lr = 0.0001#学习率learn rate
iteration = 100000#迭代次数
loss_history = []#
#开始迭代
for i in range(iteration):
    l_result = 0.0
    for n in range(len(x_data)):
        l_result = l_result + (y_data[n]-(u*x_data[n]+w))**2
    loss_history.append(l_result)#记录误差值
    #开始移动的方向
    u_grade = 0.0
    w_grade = 0.0
    for n in range(len(x_data)):#计算偏微分
        u_grade = u_grade - 2.0*(y_data[n]-u*x_data[n]-w)*x_data[n]
        w_grade = w_grade - 2.0*(y_data[n]-u*x_data[n]-w)
   
    u = u - lr*u_grade#向最小值移动
    w = w - lr*w_grade#向最小值移动

程序运算结果：u=-0.0242；w=4.809；loss=60.5515
结果如图：橙色为预测结果

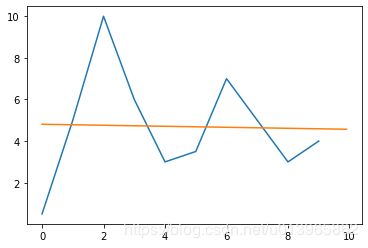
显然预测结果过于粗糙，模型为：y=-0.0242x + 4.809;预测下一个值为：4.567

实例二：三元模型预测结果

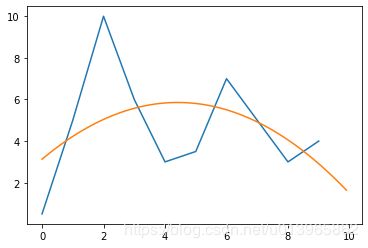
假设数据符合模型：y=vx^2 + ux + w
Loss=∑(y_data[n]-(v * x_data[n]^2+u * x_data[n]+w)) ^2
同样需找到Loss最小时v u w 的值：

import numpy as np
import matplotlib.pyplot as plt
x_data=[x for x in range(10)]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]
plt.plot(x_data,y_data)
#随即给出v u w的初始值
v= 1
u= 1
w= -2
lr = 0.0001
iteration = 100000
loss_history = []
for i in range(iteration):
    l_result = 0.0
    for n in range(len(x_data)):
        l_result = l_result + (y_data[n]-(v*x_data[n]**2+u*x_data[n]+w))**2
    
    loss_history.append(l_result)
    v_grade = 0.0
    u_grade = 0.0
    w_grade = 0.0
    for n in range(len(x_data)):
        v_grade = v_grade - 2.0*(y_data[n]-v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**2)
        u_grade = u_grade - 2.0*(y_data[n]-v*x_data[n]**2 - u*x_data[n]-w)*x_data[n]
        w_grade = w_grade - 2.0*(y_data[n]-v*x_data[n]**2 - u*x_data[n]-w)
  
    v = v - lr*v_grade*0.001 #为了调整该方向移动速度
    u = u - lr*u_grade
    w = w - lr*w_grade

运行结果：v=-0.13996；u=1.235；w=3.1299；Loss=50.18
确实样本误差更小了，但是预测结果并不理想：
y=-0.13996x^2 + 1.235x +3.1299；预测下一个值为：1.48

实例三：四元模型预测结果

假设数据符合模型：y=cx^ 3 + vx^ 2 + u*x + w
Loss= (y_data[n]-(c * x_data[n]^3+v * x_data[n]^2+u * x_data[n]+w))^ 2
同样需找到Loss最小时c v u w 的值：

import numpy as np
import matplotlib.pyplot as plt
x_data=[x for x in range(10)]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]
plt.plot(x_data,y_data)

c= 0.04
v= -0.65
u= 2.95
w= 2.25

lr = 0.0001
iteration = 100000
loss_history = []

for i in range(iteration):
    l_result = 0.0
    for n in range(len(x_data)):
        l_result = l_result + (y_data[n]-(c*x_data[n]**3+v*x_data[n]**2+u*x_data[n]+w))**2
    
    loss_history.append(l_result)
    
    c_grade = 0.0
    v_grade = 0.0
    u_grade = 0.0
    w_grade = 0.0
    for n in range(len(x_data)):
        c_grade = c_grade - 2.0*(y_data[n]-c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**3)
        v_grade = v_grade - 2.0*(y_data[n]-c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**2)
        u_grade = u_grade - 2.0*(y_data[n]-c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)* x_data[n]
        w_grade = w_grade - 2.0*(y_data[n]-c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)
    
    c = c - lr*c_grade*0.00001
    v = v - lr*v_grade*0.001
    u = u - lr*u_grade
    w = w - lr*w_grade

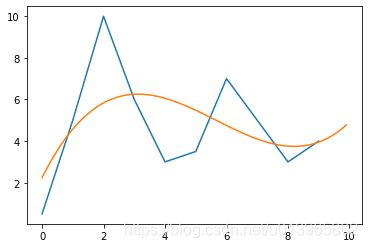
运行结果：c=0.0431；v=-0.71643；u=3.17539；w=2.1069；Loss=39.75
确实样本误差更小了，预测结果比较合理：
y=0.0431x^3-0.71643x2 + 3.17539x +2.1069；预测下一个值为：5.3178
如下图所示：

实例四：五元模型预测结果

假设数据符合模型：y=b* x^ 4 + c* x^ 3 + v* x^ 2 + u*x + w
Loss= (y_data[n]-(b * x_data[n]^ 4+c * x_data[n]^3+v * x_data[n]^2+u * x_data[n]+w))^ 2
同样需找到Loss最小时b c v u w 的值：

import numpy as np
import matplotlib.pyplot as plt

x_data=[x for x in range(10)]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]

plt.plot(x_data,y_data)

#随机给出初始值
b= 0.002531
c= 0.00673
v= -0.591
u=3.198
w= 1.9092

lr = 0.0001
iteration = 100000
loss_history = []


for i in range(iteration):
    l_result = 0.0
    for n in range(len(x_data)):
        l_result = l_result + (y_data[n]-(b*x_data[n]**4+c*x_data[n]**3+v*x_data[n]**2+u*x_data[n]+w))**2
    
    loss_history.append(l_result)

    b_grade = 0.0
    c_grade = 0.0
    v_grade = 0.0
    u_grade = 0.0
    w_grade = 0.0
    for n in range(len(x_data)):
        b_grade = b_grade - 2.0*(y_data[n]-b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**4)
        c_grade = c_grade - 2.0*(y_data[n]-b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**3)
        v_grade = v_grade - 2.0*(y_data[n]-b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**2)
        u_grade = u_grade - 2.0*(y_data[n]-b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)* x_data[n]
        w_grade = w_grade - 2.0*(y_data[n]-b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)
    
    b = b - lr*b_grade*0.0001
    c = c - lr*c_grade*0.00001
    v = v - lr*v_grade*0.001
    u = u - lr*u_grade
    w = w - lr*w_grade

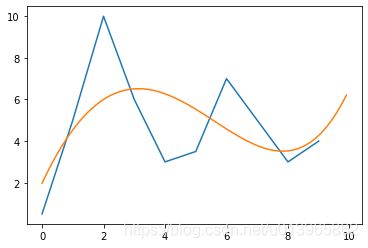
运行结果：b= 0.002108；c=0.011897；v=-0.598699；u=3.1427；w=1.9788；Loss=41.17
样本误差更大了，预测结果较合理：
y= 0.002108x^ 4+0.011897x^ 3-0.598699x^2 + 3.1427x +1.9788；预测下一个值为：6.51
如下图所示：

实例五：六元模型预测结果

假设数据符合模型：y=k* x^ 5+b* x^ 4 + c* x^ 3 + v* x^ 2 + u*x + w
Loss= (y_data[n]-(k * x_data[n]^ 5+b * x_data[n]^ 4+c * x_data[n]^3+v * x_data[n]^2+u * x_data[n]+w))^ 2
同样需找到Loss最小时k b c v u w 的值：

import numpy as np
import matplotlib.pyplot as plt

x_data=[x for x in range(10)]
y_data=[0.5,5,10,6,3,3.5,7,5,3,4]

k= -0.000980
b= 0.014671
c= 0.00034766
v= -0.850866
u= 3.684875
w= 2.02065

lr = 0.0001
iteration = 1000000
loss_history = []
for i in range(iteration):
    l_result = 0.0
    for n in range(len(x_data)):
        l_result = l_result + (y_data[n]-(k*x_data[n]**5+b*x_data[n]**4+c*x_data[n]**3+v*x_data[n]**2+u*x_data[n]+w))**2
    
    loss_history.append(l_result)
    
    
    k_grade = 0.0
    b_grade = 0.0
    c_grade = 0.0
    v_grade = 0.0
    u_grade = 0.0
    w_grade = 0.0
    for n in range(len(x_data)):
        k_grade = k_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**5)
        b_grade = b_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**4)
        c_grade = c_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**3)
        v_grade = v_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)*(x_data[n]**2)
        u_grade = u_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)* x_data[n]
        w_grade = w_grade - 2.0*(y_data[n]-k*(x_data[n])**5 - b*(x_data[n])**4 - c*x_data[n]**3 - v*x_data[n]**2 - u*x_data[n]-w)
   
    k = k - lr*k_grade*0.0000001
    b = b - lr*b_grade*0.0001
    c = c - lr*c_grade*0.00001
    v = v - lr*v_grade*0.001
    u = u - lr*u_grade
    w = w - lr*w_grade

运行结果：k=-0.002328；b= 0.03316；c=-0.011216；v=-1.49945；u=5.75026；w=1.1103288；Loss=30.21
样本误差最小，预测结果偏差较大：
如下图所示：

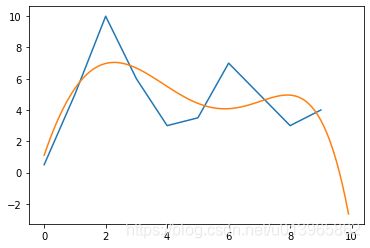
此为过度拟合！