python 树（二叉树，搜索树，平衡树，红黑树，B树）

python 树（二叉树，搜索树，平衡树，红黑树，B树）
树—一种典型的非线性结构
节点深度是指从根节点到该结点的路径长度
节点高度是该节点到叶子结点的路径长度
树的高度是指从根节点到树中最深叶子节点的长度（只含有根节点，高度为0）
树的高度，是树中所有节点高度的最大值
树的深度，是树中所有节点深度的最大值
对于同一棵树，其深度高度相同，但各个节点，其深度高度不一定相同

二叉树：由根节点和两棵不相交的子树（分别称为左子树和右子树）组成
空树也是一棵有效的二叉树
二叉树–分类：
严格二叉树：二叉树中的每个节点要么有两个孩子结点，要么没有孩子结点
满二叉树：二叉树中的每个结点恰好有两个孩子结点且所有叶子结点都在同一层
完全二叉树：在遍历过程中对于空指针也赋予编号，所有叶结点的深度为h或h-1

二叉树–遍历：
前序遍历可以如下定义：
访问根节点；
按前序遍历方式遍历左子树；
按前序遍历方式遍历右子树；
中序遍历如下定义：
按中序遍历方式遍历左子树；
访问根节点；
按中序遍历方式遍历右子树；
后续遍历如下定义：
按后序遍历左子树；
按后序遍历右子树；
访问根节点；
层次遍历的定义如下：
访问根节点；
在访问第l层时，将l+1层的节点按顺序保存在队列中；
进入下一层并访问该层的所有结点；
重复上述操作直至所有层都访问完；

二叉搜索树（二叉查找树）—BST：左子树节点的元素<根节点<右子树节点的元素
左右子树不为空，任意节点的左右子树分别是二叉查找树
没有键值相等的节点
一个二叉查找树由n个节点随机构成，对于某些情况，二叉查找树会退化成一个有n个节点的线性链（根最小或者最大）
在二叉查找树的基础上,又出现了AVL树,红黑树
注意：对二叉查找树进行中序遍历，得到有序集合。
平衡二叉树（AVL树）
一棵空树
左右两个子树的高度差（平衡因子）的绝对值不超过1
左右两个子树都是一棵平衡二叉树
平衡二叉树必定是二叉查找树，反之不一定
平衡因子（平衡度）：结点的平衡因子是结点的左子树的高度减去右子树的高度。（或反之定义）
平衡二叉树的目的是为了减少二叉查找树层次，提高查找速度
平衡二叉树的常用实现方法有AVL、红黑树、替罪羊树、Treap、伸展树等
AVL树适合用于插入删除次数比较少，但查找多的情况。
维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多，
更多的地方是用追求局部而不是非常严格整体平衡的红黑树.
当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树.

红黑树（ R-B Tree）（Red-Black Tree）—一种二叉查找树（弱平衡二叉树）
在每个节点增加一个存储位表示节点颜色（可以是red或者black）
红黑树没有一条路径会比其他路径长出两倍
弱平衡二叉树–相同节点情况下AVL树的高度低于红黑树
相对于AVL树，旋转次数变少，适用于搜索，插入，删除操作多情况
特点：每个节点非红即黑
根节点是黑色
每个叶节点（叶节点即树尾端NIL指针或NULL节点）都是黑的
如果某一节点红色，两儿子都是黑色
任意节点，其到叶子节点树NIL指针的每条路径都包含相同数目的黑节点（每条路径都包含相同的黑节点.）
时间复杂度O（logN）–N是树中元素数目，存储有序数据，效率高
应用
广泛用于C++的STL中,map和set都是用红黑树实现的.
著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,
每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间.
IO多路复用epoll的实现采用红黑树组织管理sockfd，以支持快速的增删改查.
ngnix中,用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.
java中TreeMap的实现.

B-树==B树（-只是一个符号）
一种平衡多路查找树（相对于二叉,B树每个内节点有多个分支）
在相同的的节点的情况下,一颗B/B+树的高度远远小于红黑树的高度–
–B/B+树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成,而CPU的速度非常快,
所以B树的操作效率取决于访问磁盘的次数,关键字总数相同的情况下B树的高度越小，磁盘I/O所花的时间越少.
特点：根节点儿子数[2,M]
任意非叶子节点最多只有M个儿子；M>2
除根节点以外的非叶子节点的儿子数为[M/2,M]
每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
非叶子结点的关键字个数=指向儿子的指针个数-1
非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]
非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，
P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树
所有叶子结点位于同一层

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果
命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为
空，或已经是叶子结点；

B-树的特性：
1.关键字集合分布在整颗树中；
2.任何一个关键字出现且只出现在一个结点中；
3.搜索有可能在非叶子结点结束；
4.其搜索性能等价于在关键字全集内做一次二分查找；
5.自动层次控制；

B+树的特性：
B+ 树是一种树数据结构，是一个n叉树，每个节点通常有多个孩子，
一棵B+树包含根节点、内部节点和叶子节点。
根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩子节点的节点。
B+树—B树的变形树–（文件目录一级一级索引，只有最底层叶子结点（文件））保存数据
文件查找—非叶子节点只保存索引，不保存实际数据，数据都保存在叶子节点
所有非叶子节点都可以看成索引部分
B+树的性质(下面提到的都是和B树不相同的性质)
非叶子节点的子树指针与关键字个数相同;
非叶子节点的子树指针p[i],指向关键字值属于[k[i],k[i+1]]的子树.(B树是开区间,也就是说B树不允许关键字重复,B+树允许重复)；
为所有叶子节点增加一个链指针.
所有关键字都在叶子节点出现(稠密索引). (且链表中的关键字恰好是有序的);
非叶子节点相当于是叶子节点的索引(稀疏索引),叶子节点相当于是存储(关键字)数据的数据层.
更适合于文件系统;
B和B+树主要用在文件系统以及数据库做索引.比如Mysql;
B+ 树通常用于数据库和操作系统的文件系统中。NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。
B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入。
（M=3）
B/B+树性能分析：
n个节点----平衡二叉树高度为H（logn）
B/B+树高度为logt((n+1)/2)+1
若要作为内存中的查找表,B树却不一定比平衡二叉树好,尤其当m较大时更是如此.
因为查找操作CPU的时间在B-树上是O(mlogtn)=O(lgn(m/lgt)),而m/lgt>1;
所以m较大时O(mlogtn)比平衡二叉树的操作时间大得多. 因此在内存中使用B树必须取较小的m.
（通常取最小值m=3，此时B-树中每个内部结点可以有2或3个孩子，这种3阶的B-树称为2-3树）
为什么说B+tree比B树更适合实际应用中操作系统的文件索引和数据索引.
B±tree的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,
如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,
一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了.
由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。
所以任何关键字的查找必须走一条从根结点到叶子结点的路。
所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
ps:我在知乎上看到有人是这样说的,我感觉说的也挺有道理的:
他们认为数据库索引采用B+树的主要原因是:
B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,
B+树应用而生.B+树只需要去遍历叶子节点就可以实现整棵树的遍历.
而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作（或者说效率太低）.
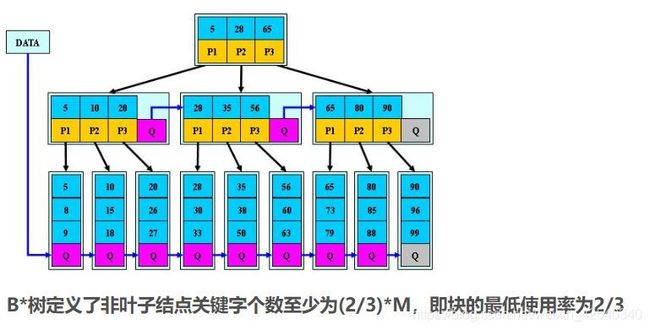
B*树：是B+树的变体，在B+树的非根和非叶子节点再增加指向兄弟的指针
B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据

复制到新结点，
最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父

结点，而不会影响兄弟结点，
所以它不需要指向兄弟的指针；

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，
那么将一部分

数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字

（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之

间增加新结点，
并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；
小结：

B-树：

多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键

字范围的子结点；

所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：

在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点

中出现，
非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：
在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率

从1/2提高到2/3；